Les équations et inéquations : cours de maths en seconde (2de)

Sommaire de cette fiche

1 0. Introduction
2 I. Résolution exacte d’ équations et d’inéquations
- 2.1 1. Equation et inéquation du 1er degré
- 2.2 2. Les équations-produits :
3 II. Résolution approchée d’équations et d’inéquations
4 Vous avez assimilé ce cours sur les équations, les inéquations et la résolution graphique en 2de?

La résolution d’équations et d’inéquations dans un cours de maths en 2de où nous résolvons des équations par le calcul puis par la méthode graphique.

Connaissances du collège nécessaires à ce chapitre.

Vérifier qu’un nombre est solution d’une équation;
Vérifier qu’un nombre est solution d’une inéquation;
Résoudre des équations simples;
Résoudre des inéquations simples.

0. Introduction

Quelle est la différence entre une égalité et une équation ?

Une égalité est une affirmation qui utilise le symbole = et qui peut être que vraie ou fausse.Par exemple, $3\times \,4=12$ est une égalité qui est vraie, et $\pi=3,14$ est une égalité qui est fausse.

Une équation est une égalité dans laquelle se trouve un nombre inconnu, généralement noté .

I. Résolution exacte d’ équations et d’inéquations

La résolution algébrique d’une équation ou d’une inéquation permet de trouver la valeur exacte de chacune des solutions.

1. Equation et inéquation du 1er degré

Propriété : opérations sur les équations.

Les opérations suivantes ne changent pas l’ensemble des solutions d’une équation :

additionner un même nombre aux deux membres d’une équation ;
multiplier par un même nombre non nul les deux membres d’une équation.

Propriété : opérations sur les inéquations.

Les opérations suivantes ne changent pas l’ensemble des solutions d’une inéquation :

additionner un même nombre aux deux membres d’une inéquation ;
multiplier par un même nombre positif non nul les deux membres d’une inéquation ;
multiplier par un même nombre négatif non nul les deux membres d’une inéquation
à condition d’inverser le sens de l’inégalité.

Méthode : résoudre un problème algébriquement.

1. On détermine et dénomme l’inconnue.
2. On interprète les informations sous forme d’une (in)équation.
3. On résout l’(in)équation en utilisant les règles précédentes :
  - on regroupe les termes contenant l’inconnue dans le même membre de l’(in)équation ;
  - si nécessaire, on réduit les expressions des deux membres ;
  - on isole l’inconnue dans l’ordre inverse des priorités de calcul.

On répond au problème posé par une phrase. La résolution de l’(in)équation peut faire apparaître des solutions correctes mathématiquement,mais incohérentes avec le problème.

Exemple :
Le cinéma d’art et d’essai de Mathyville propose une carte d’abonnement annuelle à 15 € et la
séance coûte alors 6,40 € au lieu de 9 €.

Rania hésite à s’abonner.
À combien de séances dans l’année doit-elle assister au minimum pour que l’abonnement devienne intéressant ?

Correction
1) On désigne par x le nombre de séances de cinéma auxquelles Rania ira cette année.
2) Avec l’abonnement cela coûterait : 15 + 6,4x.
Sans l’abonnement cela coûterait : 9x. Pour que l’abonnement soit intéressant, il suffit que
15 + 6, 4x < 9x.

3) Lors de la résolution qui suit, chaque étape est équivalente à la précédente.
$15\,+\,6,\,4x\,-\,6,\,4x\,<9x-\,6,\,4x$
$15\,<\,2,\,6x$

$\frac{15}{2,\,6}\,<\,\frac{2,\,6x}{2,\,6}$

$\frac{15}{2,6}<x$

Les solutions de cette inéquation sont les nombres de l’intervalle $]\frac{15}{2,6};+\infty[$ .
4) Or, $\frac{15}{2,6}\simeq\,5,8$ . Les solutions du problème sont les nombres entiers supérieurs ou égaux à 6.
Donc il suffit que Rania aille au cinéma au moins 6 fois dans l’année pour que l’abonnement
soit intéressant.

2. Les équations-produits :

Propriété :

Un produit est nul si et seulement si au moins l’un de ses facteurs est nul.

Méthode : obtenir et résoudre une équation-produit.
Pour résoudre une équation plus complexe, on obtient puis résout une équation-produit.
1) On se ramène à une équation ayant un membre nul.
2) On factorise l’expression littérale.
3) On résout l’équation produit obtenue.

Exemple :
Dans un repère, on représente f définie par $f\,(x)\,=\,3(x\,-7)^2\,-\,12$ pour $x\,\in\,[-6;\,6]$ .
Combien de fois la courbe coupera-t-elle l’axe des abscisses ?
S’il(s) existe(nt), préciser les coordonnées de ce(s) point(s).

Correction
Les points d’intersection d’une courbe avec l’axe des abscisses sont les points de la courbe
d’ordonnée nulle.

On note x l’abscisse des points d’intersection. Ce sont donc les antécédents
de 0 et il suffit de résoudre l’équation $3(x\,-\,7)^2\,-\,12\,=\,0$ dans [−6; 6] pour les trouver.
Lors de la résolution, chaque étape est équivalente à la précédente.
1) On obtient et on simplifie une équation ayant un membre nul.
$3(x\,-\,7)^2\,-\,12\,=\,0$
$(x\,-\,7)^2\,-\,4\,=\,0$

2) On factorise en reconnaissant l’identité remarquable : $a^2\,-\,b^2\,=\,(a\,+\,b)(a\,-\,b)$ .
$(x-\,7)^2\,-\,22\,=\,0$
(x − 7 + 2)(x − 7 − 2) = 0
(x − 5)(x − 9) = 0

3) On résout l’équation produit obtenu.
x − 5 = 0 ou x − 9 = 0
x = 5 ou x = 9

4) On répond au problème posé.
Cette équation a deux solutions : 5 et 9.
Or, 9 $\notin$ [−6; 6]. La courbe représentative de la fonction f dans un repère pour $x\,\in\,[-6;\,6]$ ,
coupe l’axe des abscisses au point de coordonnées (5; 0).

Remarques :
Certaines équations ne se factorisent pas dans $\mathbb{R}$ .
Par exemple $x^2\,+\,3\,=\,0$ n’admet pas de solution réelle.
Des logiciels de calculs formels peuvent aider à la résolution d’équation.

II. Résolution approchée d’équations et d’inéquations

Quand la résolution algébrique d’une (in)équation n’est pas possible, on peut cependant
localiser et estimer des valeurs approchées.

Méthode : estimer graphiquement une solution.
1) On trouve deux fonctions f et g telles que l’équation ou l’inéquation puisse s’écrire sous la forme
f (x) = g(x) ou f (x) < g(x).
2) On trace les courbes représentatives de f et g dans un même repère.
3) On cherche les abscisses
• des points d’intersection des deux courbes pour résoudre f (x) = g(x) ;
• des points de Cf au-dessous (au-dessus) de Cg pour f (x) < g(x) ( f (x) > g(x)).

Exemple :
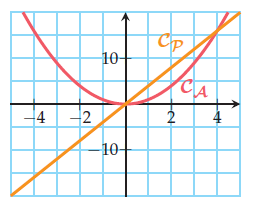
Jacques a dit que le périmètre d’un carré est toujours inférieur à son aire. A-t-il raison ?

Correction
1) On note x le côté d’un carré. Le périmètre est définie par P(x) = 4x et l’aire par A(x) = .
Répondre à la question revient à étudier l’inéquation $P(x)\,\leq\,\,A(x)$ .
2) On trace leur courbe représentative et dans un même repère.
3) Le graphique indique deux zones disjointes pour lesquelles $P(x)\,\leq\,\,A(x)$ : $]\,-\infty;\,0]$ et
[4;+\infty[ » alt= »[4;+\infty[ » align= »absmiddle » />. Donc, pour des valeurs entre 0 et 4 unités, le périmètre d’un carré est supérieur à son
aire. Jacques a tort !

Notation:

Les solutions de l’inéquation $P(x)\,\leq\,\,A(x)$ sont dans $]\,-\infty;\,0]$ ∪ [4;+\infty[ » alt= »[4;+\infty[ » align= »absmiddle » />.

Le symbole ∪ désigne la réunion des deux intervalles ; il indique qu’un nombre dans l’un ou
l’autre des deux intervalles est solution de cette inéquation.

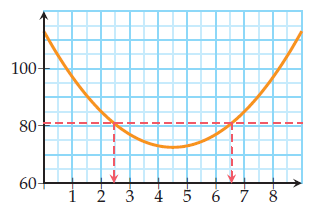
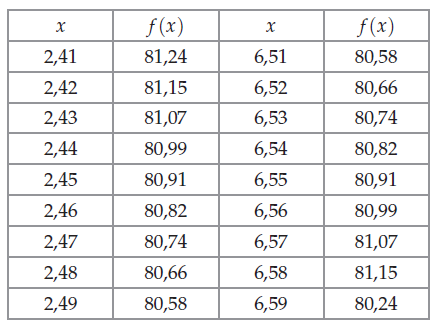
Méthode : affiner une solution.

Voici le graphique obtenu lors de la résolution de $x^2\,+\,(9\,-\,x)^2\,+\,32\,=\,81$ .
Donner des valeurs approchées à $10^{-2}$ près des solutions.

Correction
Le graphique met en évidence deux solutions
proches l’une de 2,5 et l’autre de 6,5.

On pose $f\,(x)\,=\,x^2\,+\,(9\,-\,x)^2\,+\,32$ .

Les deux solutions sont environ 2,44 cm et 6,56 cm.

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «equations, inéquations et résolution graphique : cours de maths en 2de en PDF.» au format PDF.

Réviser les leçons et les exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres utilitaires pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathovore c'est 14 081 107 cours et exercices de maths téléchargés en PDF.

Equations, inéquations et résolution graphique : cours de maths en 2de en PDF.

0. Introduction

I. Résolution exacte d’ équations et d’inéquations

1. Equation et inéquation du 1er degré

2. Les équations-produits :

II. Résolution approchée d’équations et d’inéquations

Vous avez assimilé ce cours sur les équations, les inéquations et la résolution graphique en 2de?

Résumé-Quiz

Information

Résultats

Categories

Réviser les leçons et les exercices avec nos Q.C.M :

D'autres utilitaires pour progresser en autonomie :