Les fonctions numériques : cours de maths en 2de en PDF.
Mis à jour le 31 août 2025
I. Définir une fonction numérique :
1. Ensemble R et intervalles :
L’ensemble des abscisses des points d’une droite graduée est appelé l’ensemble des nombres réels.
On note  l’ensemble de tous ces nombres.
l’ensemble de tous ces nombres.
Certaines parties de  sont appelées des intervalles; on les note en utilisant des crochets.
sont appelées des intervalles; on les note en utilisant des crochets.
| Ensemble des réels x tels que : | Intervalle | |
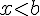 |
![]-\infty;b[](https://mathovore.fr/latex-images/b3df452312b56f3b9996f8f9d911fcc0.png) |
|
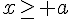 |
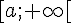 |
|
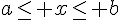 |
![[a;b]](https://mathovore.fr/latex-images/94acf62f087ab3268b2b3fa5a8a7a79c.png) |
|
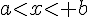 |
![]a;b[](https://mathovore.fr/latex-images/c1d56030f92b9b4b110168bbff87ebe2.png) |
|
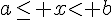 |
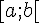 |
On définit de la même façon les intervalles ![]a;b]](https://mathovore.fr/latex-images/23e057374f81104ff9a28bda35582550.png) ,
, ![]a;+\infty[](https://mathovore.fr/latex-images/f62edbbb44b9be50287ac40d37b0a812.png) et
et ![]-\infty,b]](https://mathovore.fr/latex-images/e6cd2db0fb407be02c5c96e8eccbd0bc.png) .
.
2. Vocabulaire des fonctions numériques :
Définir une fonction  sur une partie D de
sur une partie D de  , c’est associer à tout nombre de D, un nombre unique appelé image du nombre x.
, c’est associer à tout nombre de D, un nombre unique appelé image du nombre x.
- L’image du nombre x par la fonction
 est notée f(x).
est notée f(x). - La fonction
 est parfois notée
est parfois notée - On dit que D est l’ensemble de définition de
 .
. - Si f(a)=b, on dit que a est un antécédent de b par f ou que b est l’image de a par
 .
.
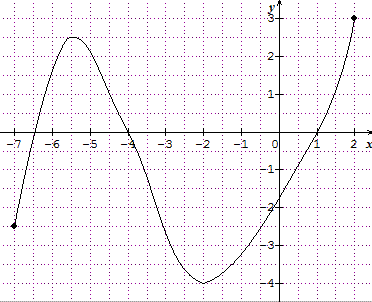
Exemple 1 : Une fonction définie par un graphique.
L’ensemble de définition de f est l’intervalle [- 7;2].
Le nombre – 5 a pour image 2 donc f(- 5 ) = 2.
Exemple 2 : une fonction g définie par un tableau de valeurs.
Le nombre 0 a une seule image 1.
g(-1)=4 et g(3)=4 donc des antécédents de 4 par g sont -1 et 3.
| Nombre x | – 4 | – 1 | 0 | 2 | 3 |
| Image g(x) | 5 | 4 | 1 | 2 | 4 |
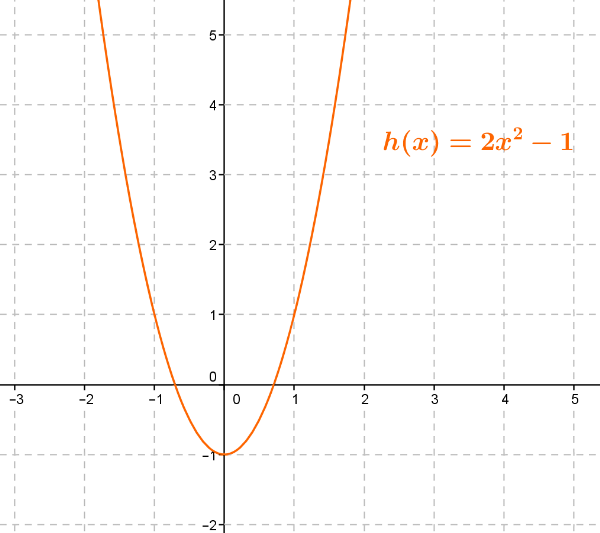
Exemple 3 : une fonction h définie par une formule algébrique.
La fonction  associe à un nombre réel
associe à un nombre réel  quelconque, le nombre
quelconque, le nombre 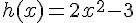 .
.
L’ensemble de définition de h est  .
.
Pour calculer l’image de – 5, on remplace  par – 5 dans l’expression de
par – 5 dans l’expression de  :
:
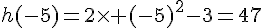 .
.
II. Courbes et résolutions graphiques :
1. Courbe représentative d’une fonction :
f est une fonction définie sur D. Dans un repère du plan, la courbe représentative (ou représentation graphique)  de f est l’ensemble des points M(x;y) dont:
de f est l’ensemble des points M(x;y) dont:
Autrement dit: M(x;y) 
 si, et seulement si, x
si, et seulement si, x 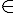 D et
D et 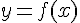 .
.
On dit que 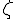 a pour équation
a pour équation 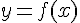 dans le repère choisi.
dans le repère choisi.
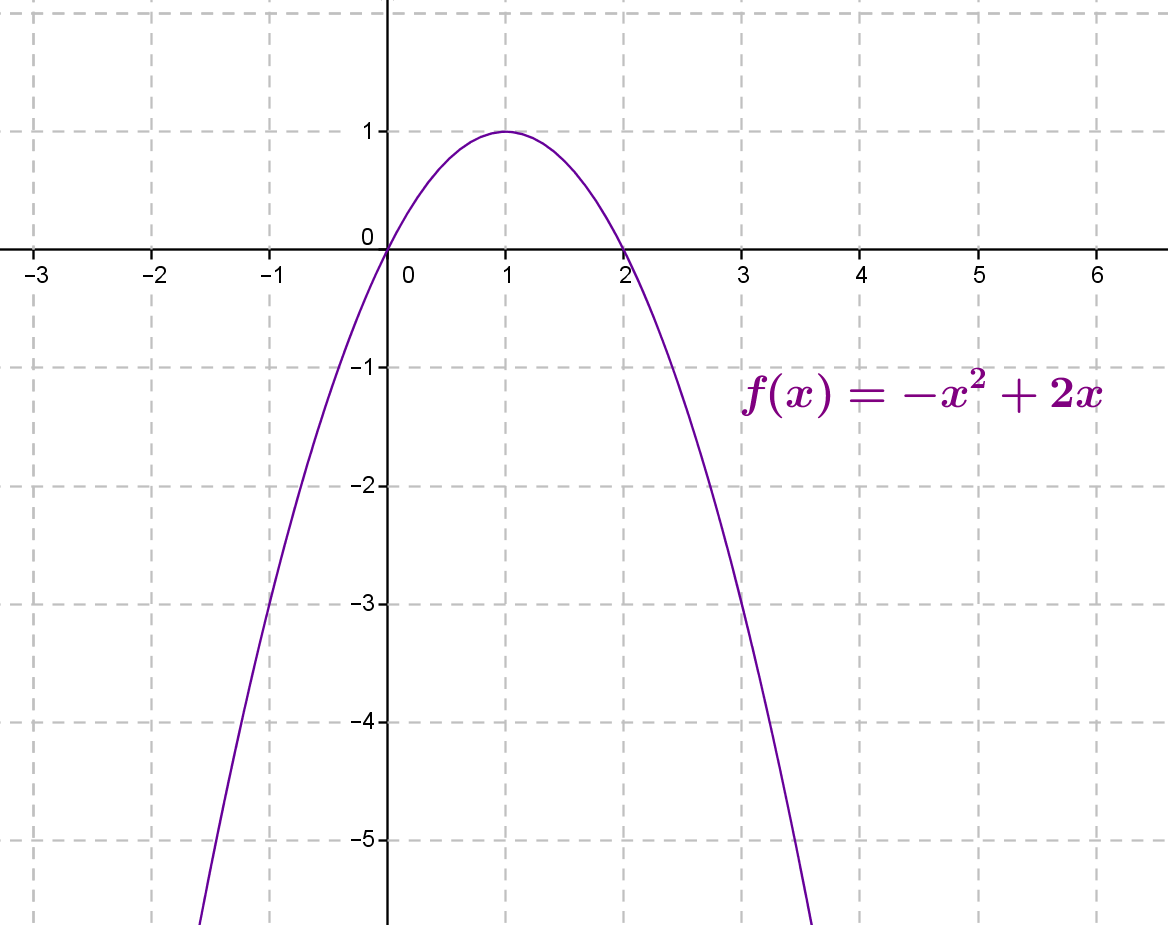
Exemple :
 est la fonction définie sur
est la fonction définie sur  par
par 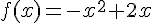 .
.
Voici la courbe représentative de cette fonction :
Le point A(2;0) appartient-il à la courbe ?
oui car 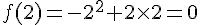 .
.
Le point B(- 2 ; – 7) appartient-il à la courbe ?
Non car 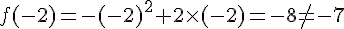 .
.
2. Résolution graphique d’équations :
Cf et Cg sont les courbes représentatives des fonctions f et g dans un repère.
a. Equations f(x)=k (avec k un réel) :
Les solutions de l’équation f(x)=k sont les abscisses des points d’intersection de la courbe Cf et de la droite y=k.
b. Equations f(x)=g(x)
les solutions de l’équation f(x)=g(x) sont les abscisses des points d’intersection des courbes Cf et Cg.
III. Sens de variation et extremums :
f est une fonction définie sur un intervalle I, de courbe représentative Cf dans un repère du plan.
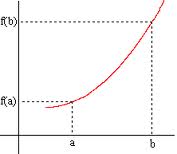
1. Fonction croissante :
Dire que f est croissante sur I signifie que pour tout nombre réel 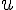 et
et 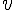 de
de 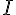 , si
, si 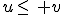 alors
alors 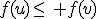 .
.
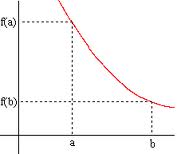
2. Fonction décroissante :
Dire que f est décroissante sur I signifie que pour tout nombre réel 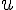 et
et 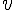 de
de 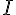 , si
, si 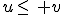 alors
alors 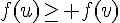 .
.
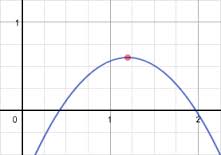
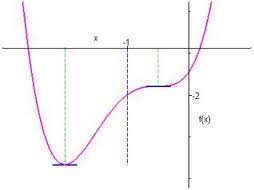
3. Extremum : maximum et minimum.
a. Maximum d’une fonction :
a désigne un nombre réel de l’intervalle I. Dire que f(a) est le maximum de f sur I signifie que, pour tout réel x de I : 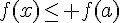 .
.
b. Minimum d’une fonction :
a désigne un nombre réel de l’intervalle I. Dire que f(a) est le minimum de f sur I signifie que, pour tout réel x de I : 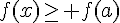 .
.
On dit que f(a) est un extremum de f sur I pour indiquer que f(a) est un maximum ou un minimum de f sur I.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «les fonctions numériques : cours de maths en 2de en PDF.» au format PDF.
Ressources de seconde
Cours de seconde
Exercices de seconde
D'autres cours et exercices à consulter
🤖 Exercices IA Interactifs ✨

Des milliers d'exercices interactifs conformes aux programmes officiels. Apprenez, pratiquez et progressez à votre rythme.
Exercices interactifsL'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.