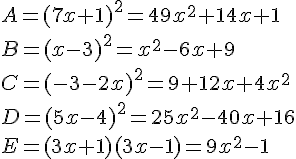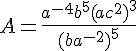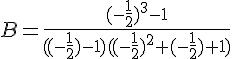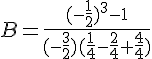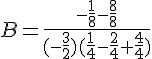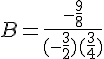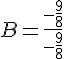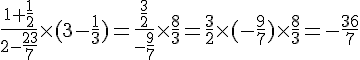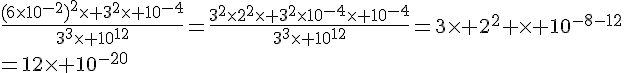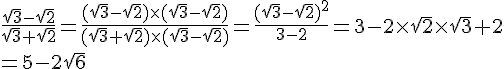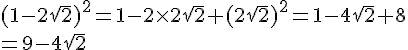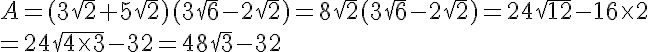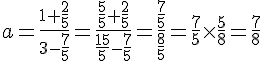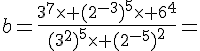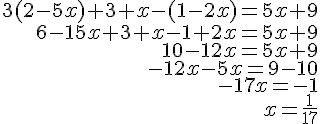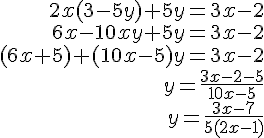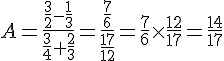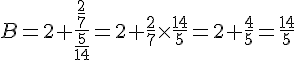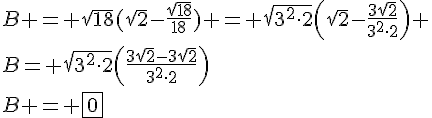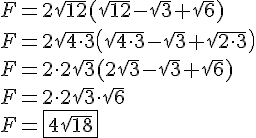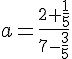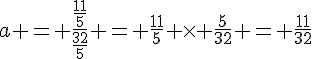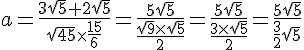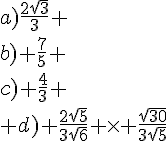Calculs et problèmes : corrigé des exercices de maths en 2de en PDF.
Mis à jour le 14 septembre 2025
Exercice 1 :
Soit
a. Montrer que
tout d’abord
Soit la fonction , cette fonction est strictement croissante sur
.
donc
ainsi
et donc
b. Calculer .
c. En déduire la valeur de Il y a deux valeurs possibles X=2 ou X=-2
or
d’après 1 X<0 , on en déduit que X = – 2 .
Exercice 2 :
Calculer :
Exercice 3 :
Exercice 4 :
1. Développer et réduire:
a= (5x+1)(2x+3)
b= (4x-5)(7x-1)
c= (2x+5)(7x-3)
d= (-4x-6)(2x-1)
2. Développer et réduire:
e= (5x+1)(2x+3)+(5x+1)(x+2)
f= (4x-5)(7x-1)-(4x-5)(3x+2)
g= (-4x-6)(2x-1)+(2x-3)(8x-11)
h= (x-8)(5+3x)-(x-8)(7-x)
Exercice 5 :
Encadrer lorsque
.
alors
Exercice 6 :
Factoriser les expressions suivantes :
Exercice 7 :
Exercice 8 :
1. Sous quelle forme s’écrit un nombre pair ?
2. Sous quelle forme s’écrit un nombre impair ?
3. Montrer que le carré d’un nombre pair est un nombre pair.
avec
Conclusion : le carré d’un nombre pair est un nombre pair .
Exercice 9 :
1. Calculer la somme de 5 entiers consécutifs.
A vous de faire quelques essais .
2. Montrer que la somme de cinq entiers consécutifs est un multiple de 5.
Soit x le plus petit des entiers .
Soit
Donc la somme de 5 entiers consécutifs est bien un multiple de 5.
Exercice 10 :
1. Calculer le produit de quatre entiers consécutifs et ajouter 1.
Que remarque-t-on ? (Faire plusieurs essais)
2x3x4x5+1=121=11²
5x6x7x8+1=1681=41²
6x7x8x9+1=3025=55²
2. Montrer que, pour tout réel x, on a :
Expliquer le résultat observé à la question 1.
Le produit de 4 nombres consécutifs plus 1 peut s’écrire comme le carré d’un nombre.
Exercice 11 :
a. Décomposer en produit de nombres premiers 220 et 284.
b. Vérifier que 220 et 284 sont amicaux.
Les diviseurs de 220 sont 1;2;4;5;10;11;20;22;44;55;110;220.
Les diviseurs de 284 sont 1;2;4;71;142;284
or calculons la somme des diviseurs sauf m :
et
Conclusion : 220 et 284 sont deux entiers amicaux.
Exercice 12 :
Ecrire sous forme d’intervalles :
Exercice 13 :
1. Hervé doit factoriser A.
Voici sa réponse :
Tester l’égalité obtenue par Hervé pour
Que peut-on en conclure ?
or si l’on remplace 0 dans l’expression de départ, nous obtenons :
Conclusion : Hervé s’est trompé lors de sa factorisation.
2. Pour factoriser A, on peut penser à écrire :
Factoriser alors correctement A.
Exercice 14 :
Factoriser chaque expression en mettant en évidence un facteur commun.
Exercice 15 :
Exercice 16 :
Exercice 17 :
Exercice 18 :
Exercice 19 :
Exercice 20 :
Le nombre d’or est le nombre .
Vérifier les égalités suivantes :
1. .
2. .
Multiplions par :
(c’est l’égalité de la question 1.)
3.
Nous savons que :
Multiplions cette égalité par :
(car
)
donc
.
Exercice 21 :
La vitesse de la lumière est estimée à m/s
et la distance moyenne Terre-Soleil à 149 millions de kilomètres.
Calculer le temps nécessaire à un signal lumineux issu de la Terre pour parvenir au
Soleil.
Exercice 22 :
Pour , calculer :
Exercice 23 :
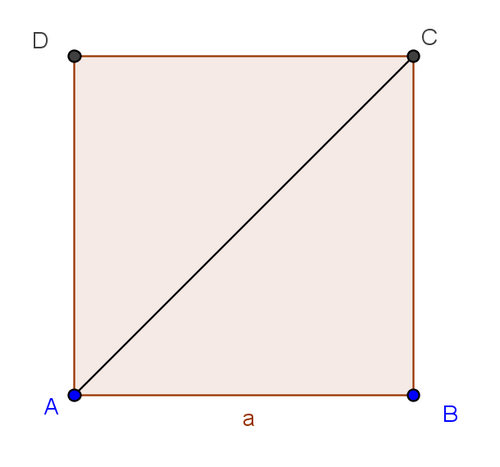
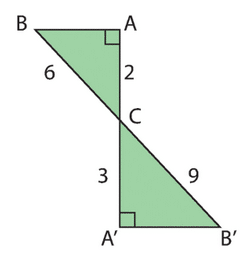
Démonter que la diagonale d’un carré de coté est
.
Dans le triangle rectangle ABC rectangle en B, d’après la partie directe du théorème de Pythagore :
(une longueur est positive ou nulle )
Exercice 24 :
Soit n un entier impair. n peut s’écrire sous la forme 2k + 1, où k est un nombre entier quelconque.
Le carré de n est donc :
n^2 = (2k+1)^2 = 4k^2 + 4k + 1 = 2(2k^2+2k) + 1.
Comme 2k^2+2k est un nombre entier, 2(2k^2+2k) est un nombre pair.
Ainsi, le carré de n est égal à un nombre pair plus 1.
Il est donc impair.
Exercice 25 :
1. 630 = 2 x 3 x 3 x 5 x 7 3150 = 2 x 3 x 3 x 5 x 7 x 5
2. \frac{3150}{630} = \frac{2 x 3 x 3 x 5 x 7 x 5}{2 x 3 x 3 x 5 x 7} = 5
3. PGCD(630 ; 3150) = 2 x 3 x 3 x 5 x 7 = 630
Exercice 26 :
Exercice 27 :
1. Soit k un entier naturel dont le nombre des dizaines est a.
Si k = a5, alors pour calculer k² :
– On multiplie a(a + 1) pour obtenir les dizaines du résultat.
– On ajoute 25 à la fin pour obtenir les unités du résultat.
On peut vérifier que cela fonctionne pour tous les exemples donnés. Par exemple, pour 35 :
– a = 3
– a(a+1) = 3 x 4 = 12, donc les dizaines du résultat sont 12.
– On ajoute 25 à la fin : 1225, donc le carré de 35 est 1225.
2.
k = a x 10 + 5
k² = (a x 10 + 5)²
k² = (10a)² + 2 x 10a x 5 + 5²
k² = 100a² + 100a + 25
k² = 25 x (4a² + 4a + 1)
On peut donc voir que le carré d’un multiple de 5 dont le nombre des dizaines est a est un multiple de 25 dont les dizaines sont égales à 4a(a+1). On peut vérifier que cela fonctionne pour tous les exemples donnés.
Cela fonctionne également pour le produit de deux nombres entiers à 2 chiffres dont les chiffres des dizaines sont égaux et la somme des unités est 10. Par exemple, 35 x 45 = 1575, et 3 + 5 = 8, donc les chiffres des dizaines sont bien égaux et la somme des unités est bien 10. On peut appliquer la même méthode que précédemment pour trouver le carré de ce produit.
Exercice 28 :
1. Pour chaque ligne, reconstruire la phrase en utilisant Si……alors …. ou …si et seulement si ….:
a.
SI Il pleut ALORS je prends mon parapluie.
SI I milieu de [AB] ALORS AI=BI
SI ET SEULEMENT SI
.
SI ALORS
.
SI ALORS ABC est isocèle en A.
Exercice 29 :
Pour n entier naturel, comparer les nombres suivants :
Exercice 30 :
Soient ,comparer les nombres :
Supposons que
Alors
Alors
Alors
Alors
ceci étant toujours vrai puisque
donc
Exercice 31 :
1. Compléter à l’aide des symboles
a.
b.
2. Préciser l’intervalle correspondant à :
a.
b.
c.
Exercice 32 :
a.
b.
2. Simplifier puis donner sous forme d’écriture scientifique la fraction suivante :
3. Simplifier les écritures suivantes :
a.
b.
c.
4. Donner la décomposition en produit de facteurs premiers du nombre .
Exercice 33 :
a. Indiquer la nature des nombres suivants :
: rationnel
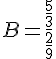
: entier D=1+
: irrationnel
b. Simplifier l’écriture du nombre suivant :
Exercice 35 :
ÉTAPE 1:
1. Dans l’exercice 1, nous devons mettre les nombres donnés sous forme irréductible et montrer les calculs.
2. Dans l’exercice 2, nous devons mettre les nombres donnés sous forme scientifique.
Forme décimale :
ÉTAPE 2:
1. Pour l’exercice 1, j’ai l’expression pour a : .
2. Je peux maintenant passer au calcul de b et c.
Résultat :
Forme décimale :
ÉTAPE 3:
1. Pour l’exercice 1, j’ai l’expression pour b : b = .
2. Je peux maintenant passer au calcul de c.
=
Résultat exact :
Approximation décimale :
20.34505208333…
ÉTAPE 4:
1. Pour l’exercice 1, j’ai l’expression pour c : .
2. Nous pouvons passer à l’exercice 2.
Résultat :
a = 520000000
ÉTAPE 5 :
1. Pour l’exercice 2, j’ai l’expression pour a : a = 520000000.
2. Je peux maintenant passer au calcul de b.
Résultat :
ÉTAPE 6 :
1. Pour l’exercice 2, j’ai l’expression pour b : .
2. J’ai maintenant les réponses finales pour les deux exercices.
Réponse finale:
Exercice 36 :
a =
b =
Exercice 37 :
Exercice 38 :
Tout d’abord, rappelons que car $9^2=81$, et que
ne peut pas être simplifié.
Nous pouvons donc simplifier la fraction :
Ensuite, nous pouvons simplifier la racine carrée :
Finalement, nous pouvons multiplier les deux résultats :
Nous ne pouvons pas simplifier davantage car et
sont premiers entre eux.
Exercice 39 :
a)
On commence par développer et simplifier l’équation :
La solution de cette équation dans est donc
.
b)
On développe et on regroupe les termes pour obtenir une équation linéaire en $y$ :
La valeur interdite pour est
, car le dénominateur
de la fraction devient alors nul.
Exercice 40 :
1.
a) L’intervalle représentant l’ensemble des réels x satisfaisant à la condition -1 ≤ x ≤ 5 est [ -1 , 5 ].
b) L’intervalle représentant l’ensemble des réels x satisfaisant à la condition 3 < x ≤ 7 est ] 3 , 7 ].
c) L’intervalle représentant l’ensemble des réels x satisfaisant à la condition x ≥ 3 est [ 3 , +∞ [.
d) L’intervalle représentant l’ensemble des réels x satisfaisant à la condition x ≤ -5 est ] -∞ , -5 ].
2.
a) Sur une droite graduée :
I = ]-∞ ; 4[ est représenté par la partie gauche de la droite, qui exclut 4 et contient tous les nombres à gauche de 4.
J = [1 ; 7] est représenté par un segment fermé de la droite allant de 1 à 7 inclus.
L’intersection de I et J est l’ensemble des nombres compris entre 1 et 4 exclus, soit ]1 ; 4[.
La réunion de I et J est l’ensemble des nombres inférieurs ou égaux à 7 et qui sont strictement à gauche de 4, soit ] -∞ ; 4 [ ∪ [1 ; 7].
b) Sur une droite graduée :
I = ]-7 ; -3] est représenté par un segment ouvert de la droite allant de -7 à -3 inclus.
J = ]-4 ; +∞[ est représenté par la partie droite de la droite, qui exclut -4 et contient tous les nombres à droite de -4.
L’intersection de I et J est l’ensemble des nombres compris entre -7 et -3 exclus, qui sont strictement à droite de -4, soit ]-4 ; -3[.
La réunion de I et J est l’ensemble des nombres qui sont inférieurs ou égaux à -3 ou qui sont strictement à droite de -4, soit ] -∞ ; -3] ∪ ]-4 ; +∞[.
Exercice 41 :
Exercice 42 :
Exercice 43 :
Exercice 44 :
Exercice 45 :
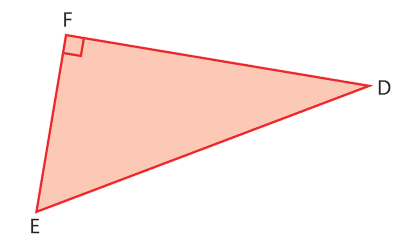
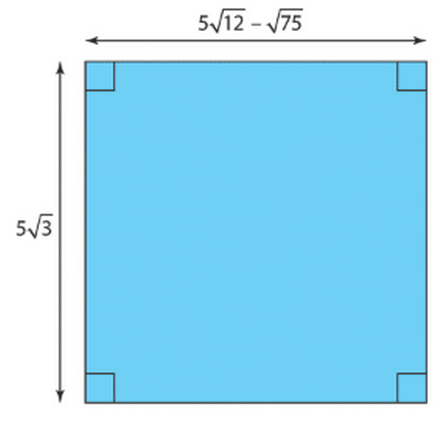
1. On utilise le théorème de Pythagore dans le triangle EDF :
On simplifie en utilisant la racine carrée :
Donc EF = cm.
2. Le périmètre du triangle EDF est la somme des longueurs des côtés :
On peut utiliser une calculatrice pour obtenir une valeur décimale approchée :
cm
Donc le périmètre du triangle EDF arrondi au millimètre est de 19,7 cm.
Exercice 46 :
1. On peut simplifier en
.
On a donc :
Donc et
2. Les côtés opposés de ABCD sont parallèles et de même longueur, donc ABCD est un parallélogramme.
3. Le périmètre est la somme des longueurs des côtés de ABCD. Le côté AB mesure , le côté BC mesure 5 cm et le côté CD mesure 8 cm.
On a car ABCD est un parallélogramme.
Finalement, le périmètre est :
L’arrondi au millimètre est donc cm.
4. L’aire de ABCD est la base AB multipliée par la hauteur correspondante, qui est la distance entre les droites (AB) et (CD).
Cette distance est la longueur de la perpendiculaire issue de A sur (CD).
On peut construire cet orthogonal en traçant la droite (AE) telle que A soit le milieu de [CE].
On obtient alors un triangle rectangle AEC en A, rectangle en E.
La longueur de CE est cm.
On utilise ensuite le théorème de Pythagore dans AEC pour calculer la hauteur AE :
On obtient cm.
Finalement, l’aire de ABCD est :
L’aire exacte est donc .
Exercice 47 :
On cherche un nombre de marches compris entre 130 et 150 qui est divisible par 3 et qui a un reste de 1 lorsqu’on le divise par 4.
Le plus petit multiple de 3 qui a un reste de 1 lorsqu’on le divise par 4 est 13 (car ).
Le plus grand multiple de 3 qui est inférieur ou égal à 150 est 147.
Donc le nombre de marches de l’escalier est 147.
Exercice 48 :
1. On a .
2. On a .
3. On a et
.
4. On peut simplifier en factorisant le numérateur et le dénominateur par
.
On obtient alors
On s’aperçoit alors que cette fraction est égale à trouvée à la question 1, donc
peut être simplifié en
.
Exercice 49 :
Voici la correspondance entre les nombres de la première ligne et les ensembles indiqués dans la première colonne :
Explication :
– Le nombre est un nombre rationnel positif car il peut être écrit sous la forme d’un fraction irréductible. Il appartient donc à l’ensemble des nombres naturels (
).
– Le nombre est également un nombre rationnel car il peut être écrit sous la forme d’une fraction. Il appartient donc à l’ensemble des nombres rationnels (
).
– Le nombre est un nombre rationnel car il peut être écrit sous la forme d’une fraction irréductible. Il appartient donc à l’ensemble des nombres rationnels (
).
– Le nombre est un nombre irrationnel car il contient une racine carrée qui ne peut pas être exprimée sous la forme d’une fraction. Il appartient donc à l’ensemble des nombres réels (
).
– Le nombre est un nombre irrationnel car il est une approximation de la constante
, qui est un nombre irrationnel. Il appartient donc à l’ensemble des nombres réels (
).
– Le nombre est un nombre rationnel négatif car il peut être écrit sous la forme d’une fraction irréductible. Il appartient donc à l’ensemble des nombres rationnels (
).
Exercice 50 :
a) Pour mettre a sous forme irréductible, nous devons simplifier les fractions présentes dans l’expression.
Pour simplifier la fraction , nous devons trouver un dénominateur commun. Dans ce cas, le dénominateur commun est 5. Ainsi, nous obtenons :
De même, pour simplifier la fraction , nous trouvons un dénominateur commun de 5 :
Maintenant, nous pouvons réécrire l’expression initiale en utilisant ces simplifications :
Donc, le nombre a peut être mis sous forme irréductible comme .
b) Pour mettre b sous forme irréductible, nous devons simplifier la fraction .
Nous pouvons simplifier les termes en utilisant les propriétés des exposants :
En utilisant les valeurs des exposants, nous obtenons :
Maintenant, nous pouvons simplifier cette fraction en trouvant un facteur commun :
Donc, le nombre b peut être mis sous forme irréductible comme .
c) Pour mettre c sous forme irréductible, nous devons simplifier la fraction .
En utilisant les propriétés des exposants, nous pouvons simplifier cette fraction :
Nous pouvons simplifier davantage en utilisant les propriétés des exposants :
Maintenant, nous pouvons simplifier cette fraction en utilisant les valeurs des exposants :
En simplifiant davantage, nous obtenons :
Maintenant, nous pouvons simplifier cette fraction en trouvant un facteur commun :
Donc, le nombre c peut être mis sous forme irréductible comme .
Exercice 51 :
a) Pour mettre le nombre sous la forme x \times 10^p, nous devons trouver une valeur de x entre 1 et 10 (non inclus) et une valeur entière p.
Tout d’abord, nous pouvons simplifier la fraction \frac{3}{25} en multipliant le numérateur et le dénominateur par 4 pour obtenir des valeurs entières :
En simplifiant davantage, nous obtenons :
Maintenant, nous avons (qui est entre 1 et 10) et
. Donc, le nombre a peut être écrit sous la forme
comme
.
b) Pour mettre le nombre sous la forme
, nous devons également trouver une valeur de x entre 1 et 10 (non inclus) et une valeur entière négative p.
Nous pouvons simplifier la fraction en multipliant le numérateur et le dénominateur par 1000 pour obtenir des valeurs entières :
En simplifiant davantage, nous obtenons :
Maintenant, nous pouvons simplifier cette fraction en trouvant une valeur entière pour :
Nous avons (qui est entre 1 et 10) et
. Donc, le nombre
peut être écrit sous la forme
comme
.
Exercice 52 :
Pour calculer et simplifier l’expression , nous allons suivre les étapes suivantes :
1. Simplifier les racines carrées :
ne peut pas être simplifié car il n’y a pas de facteur carré parfait dans 5.
2. Simplifier l’expression dans le dénominateur :
Maintenant, nous pouvons réécrire l’expression initiale en utilisant ces simplifications :
En simplifiant davantage, nous obtenons :
Maintenant, nous pouvons simplifier cette expression en simplifiant les racines carrées de 5 :
Donc, l’expression a se simplifie à .
Exercice 53 :
a) Pour résoudre cette équation, commençons par simplifier et réorganiser les termes :
Maintenant, développons les expressions entre parenthèses et simplifions les termes similaires :
Regroupons les termes similaires du côté gauche de l’équation :
Maintenant, déplaçons tous les termes avec des x d’un côté de l’équation et les constantes de l’autre côté :
Maintenant, isolons x en divisant des deux côtés par 19 :
Donc, la solution de l’équation a) est .
b) Pour résoudre cette équation quadratique, commençons par réorganiser les termes :
Maintenant, divisons toute l’équation par 5 pour simplifier :
Pour résoudre cette équation quadratique, nous pouvons utiliser la formule quadratique :
ou
Dans cette équation, . Plaçons ces valeurs dans la formule :
ou
ou
ou
ou
ou
Maintenant, simplifions davantage en divisant tous les termes par (ce qui est la même chose que de multiplier par
) :
ou
Donc, les solutions de l’équation b) sont et
.
Exercice 54 :
- Pour décomposer 204 et 595 en produits de facteurs premiers, vous pouvez utiliser la méthode de la factorisation. Voici comment vous pouvez le faire :
Décomposition en facteurs premiers de 204 : (204 est divisible par 2)
(102 est également divisible par 2)
(51 est divisible par 3 et 17 est un nombre premier)
Donc, la décomposition en facteurs premiers de 204 est : .
Décomposition en facteurs premiers de 595 :
(595 est divisible par 5)
(119 est divisible par 7 et 17 est un nombre premier)
Donc, la décomposition en facteurs premiers de 595 est : .
- Pour simplifier la fraction
, nous pouvons simplifier en utilisant les facteurs premiers trouvés précédemment.
et
Maintenant, nous pouvons annuler les facteurs communs dans le numérateur et le dénominateur :
Les facteurs premiers « 17 » se simplifient :
Maintenant, multiplions les facteurs restants dans le numérateur et le dénominateur :
204/595 = 12/35
Donc, la fraction simplifiée est
.
a)
b)
c)
d)
Exercice 55 :
Pour compléter les expressions :
a)
b)
c)
d)
Exercice 56 :
a)
b)
c)
d)
e)
f)
Exercice 57 :
a) Pour effectuer cette soustraction, nous devons trouver un dénominateur commun pour les fractions. Le dénominateur commun de 75 et 30 est 150.
Donc, nous avons :
Maintenant, nous pouvons soustraire les deux fractions :
Pour simplifier cette fraction, nous pouvons diviser le numérateur et le dénominateur par leur plus grand commun diviseur, qui est 2 :
Donc, le résultat de l’opération est .
b) Pour effectuer cette addition, nous devons ajouter les deux fractions. Les dénominateurs sont déjà les mêmes, donc nous pouvons simplement ajouter les numérateurs :
Pour simplifier cette fraction, nous pouvons diviser le numérateur et le dénominateur par leur plus grand commun diviseur, qui est 2 :
Donc, le résultat de l’opération est .
c) Pour effectuer cette soustraction, nous devons trouver un dénominateur commun pour les fractions. Le dénominateur commun de -25 et 25 est 25.
Donc, nous avons :
Maintenant, nous pouvons soustraire les deux fractions :
Pour simplifier cette fraction, nous pouvons diviser le numérateur et le dénominateur par leur plus grand commun diviseur, qui est 1 :
Donc, le résultat de l’opération est .
d) Pour effectuer cette addition, nous devons trouver un dénominateur commun pour les fractions. Le dénominateur commun de 27 et 108 est 108.
Donc, nous avons :
Maintenant, nous pouvons ajouter les deux fractions :
Pour simplifier cette fraction, nous pouvons diviser le numérateur et le dénominateur par leur plus grand commun diviseur, qui est 1 :
Donc, le résultat de l’opération est .
Exercice 58 :
ÉTAPE 1:
1. Pour simplifier les expressions et obtenir la racine carrée d’une fraction irréductible, nous devons simplifier séparément les racines carrées du numérateur et du dénominateur.
2. Nous pouvons simplifier les racines carrées en trouvant des facteurs carrés parfaits.
3. Simplifions chaque expression étape par étape.
a)
– La racine carrée de 12 peut être simplifiée comme suit :
– La racine carrée de 9 est 3.
– L’expression devient donc
b)
– La racine carrée de 147 peut être simplifiée comme suit :
– La racine carrée de 75 peut être simplifiée comme suit :
– L’expression devient donc
– Les racines carrées de 3 s’annulent, nous laissant
c)
– La racine carrée de 5 est déjà sous sa forme la plus simple.
– La racine carrée de 20 peut être simplifiée comme suit :
– Par conséquent, l’expression devient
– Les racines carrées de 5 s’annulent, nous laissant
– En simplifiant encore, on obtient
d)
– La racine carrée de \frac{28}{42} peut être simplifiée comme suit :
– La racine carrée de 30 est déjà sous sa forme la plus simple.
– La racine carrée de 45 peut être simplifiée comme suit :
ÉTAPE 2:
a)
b)
c)
d)
Réponse finale:
Exercice 59 :
ÉTAPE 1 :

2. Pour déterminer les diviseurs de 30 et 24, nous pouvons lister tous les nombres qui se divisent uniformément en chaque nombre.
diviseurs de 30=
Diviseurs :
1 | 2 | 3 | 5 | 6 | 10 | 15 | 30 (8 diviseurs)
ÉTAPE 2 :
1. Les diviseurs de 30 sont 1, 2, 3, 5, 6, 10, 15 et 30.
diviseurs de 24=
Diviseurs :
1 | 2 | 3 | 4 | 6 | 8 | 12 | 24 (8 diviseurs)
ÉTAPE 3 :
1. Les diviseurs de 24 sont 1, 2, 3, 4, 6, 8, 12 et 24.
pgcd(30 24)=
Résultat : 6
ÉTAPE 4:
1. Le plus grand diviseur commun (PGCD) de 30 et 24 est 6.
2. Le nombre de bouquets qu’il peut réaliser au maximum est égal au PGCD, qui est de 6.
3. La composition de chaque bouquet serait de 5 tulipes et 4 muscaris.
Réponse finale : Il peut réaliser un maximum de 6 bouquets, chaque bouquet contenant 5 tulipes et 4 muscaris.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «calculs et problèmes : corrigé des exercices de maths en 2de en PDF.» au format PDF.
Ressources de seconde
Cours de seconde
D'autres cours et exercices à consulter
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.



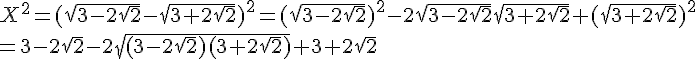
![-5<x\leq\,\, 2\,:\,x\in]-5;2]\x\geq\,\, \frac{3}{2}\,:\,[\frac{3}{2};+\infty[\x\leq\,\, -\frac{1}{4}\,:\,]-\infty;-\frac{1}{4}]\x>-5\,et\,x\leq\,\, 3,5\,:\,]-5;3,5]](https://mathovore.fr/latex-images/5cbcd88e9f2ac83ae459df304f5b211f.png)
![A=9a+15=3\times 3a+3\times 5=3(3a+5)\B=3x^2-15x=3x\times x-3x\times 5=3x(x-5)\C=8x-x^2(5x-1)=x(8-x(5x-1))\D=(3x-2)^2-(2x-1)(3x-2)\=(3x-2)[(3x-2)-(2x-1)]\=(3x-2)(3x-2-2x+1)=(3x-2)(x-1)](https://mathovore.fr/latex-images/6fdbe496092f362e288633386fb10200.png)