Calculs et problèmes : exercices de maths en 2de corrigés en PDF.
Mis à jour le 23 décembre 2025
Exercice 1 – Etude d’une expression complexe
Soit
a. Montrer que
b. Calculer .
c. En déduire la valeur de
Exercice 2 – Calculs sur les puissances
Calculer :
Exercice 3 – Calculs avec des fractions
Calculer les fractions suivantes et donner le résultat sous forme d’une fraction irréductible.
Exercice 4 – Développer et réduire des expressions
1. Développer et réduire:
a= (5x+1)(2x+3)
b= (4x-5)(7x-1)
c= (2x+5)(7x-3)
d= (-4x-6)(2x-1)
2. Développer et réduire:
e= (5x+1)(2x+3)+(5x+1)(x+2)
f= (4x-5)(7x-1)-(4x-5)(3x+2)
g= (-4x-6)(2x-1)+(2x-3)(8x-11)
h= (x-8)(5+3x)-(x-8)(7-x)
Exercice 5 – Encadrement et comparaisons de nombres
Encadrer lorsque
.
Exercice 6 – Le calcul littéral et factorisation
Factoriser les expressions suivantes :
Exercice 7 – Les nombres
Simplifier au maximum :
Exercice 8 – Nombres pairs et impairs
1. Sous quelle forme s’écrit un nombre pair ?
2. Sous quelle forme s’écrit un nombre impair ?
3. Montrer que le carré d’un nombre pair est un nombre pair.
Exercice 9 – Somme de cinq entiers consécutifs
1. Calculer la somme de 5 entiers consécutifs.
Que remarque-ton ? (Faire plusieurs essais)
2. Montrer que la somme de cinq entiers consécutifs est un multiple de 5.
Exercice 10 – Produit de quatre entiers consécutifs
1. Calculer le produit de quatre entiers consécutifs et ajouter 1.
Que remarque-t-on ? (Faire plusieurs essais)
2. Montrer que, pour tout réel x, on a :
Expliquer le résultat observé à la question 1.
Exercice 11 – Des entiers amicaux
Deux entiers positifs m et n sont dits amicaux, si la somme des diviseurs de m (autres
que m) est égale à n et simultanément la somme des diviseurs de n (autres que n) est égale à m.
Les plus petits nombres amicaux sont 220 et 284.
a. Décomposer en produit de nombres premiers 220 et 284.
b. Vérifier que 220 et 284 sont amicaux.
Exercice 12 – Ecrire sous la forme d’intervalle
Ecrire sous forme d’intervalles :
Exercice 13 – Hervé et le coup du 1
1. Hervé doit factoriser A.
Voici sa réponse :
Tester l’égalité obtenue pour par Hervé pour
Que peut-on en conclure ?
2. Pour factoriser A, on peut penser à écrire :
Factoriser alors correctement A.
Exercice 14 – Factoriser chaque expression
Factoriser chaque expression en mettant en évidence un facteur commun.
Exercice 15 – Développer puis réduire
Développer puis réduire :
Exercice 16 – Ecrire simplement une racine complexe
Ecrire plus simplement l’expression numérique suivante :
Exercice 17 – Supprimer des valeurs absolues
Ecrire sans barres de valeurs absolues, les nombres suivants :
Exercice 18 – Intersections d’intervalles
Ecrire plus simplement :
Exercice 19 – Simplification d’une fraction rationnelle
Simplifier :
Exercice 20 – Le nombre d’or
Le nombre d’or est le nombre .
Vérifier les égalités suivantes :
1. .
2. .
3.
Exercice 21 – Vitesse de la lumière
La vitesse de la lumière est estimée à m/s
et la distance moyenne Terre-Soleil à 149 millions de kilomètres.
Calculer le temps nécessaire à un signal lumineux issu de la Terre pour parvenir au
Soleil.
Exercice 22 – Calculer une expression littérale
Pour , calculer :
Exercice 23 – Calculer la longueur de la diagonale d’un carré
Démonter que la diagonale d’un carré de coté est
.
Exercice 24 – Démontrer que le carré d’un entier impair est un nombre impair
Démontrer que le carré d’un entier impair est un nombre impair.
Exercice 25 – Facteurs premiers et pgcd
1. Décomposer 630 puis 3150 en produit de facteurs premiers.
2. Réduire la fraction .
3. Calculer PGCD(630 ; 3150).
Exercice 26 – Racines carrées et fractions
1. Simplifier les nombres suivants en utilisant la décomposition en facteurs premiers .
2.Mettre les nombres suivants sous forme de fractions irréductibles.
Exercice 27 – Calculer le carré d’un multiple de 5
15 ² = 225 ; 25 ² = 625 ; 35 ² = 1225 ; 45 ² = 2025 ; 85 ² = 7225 ….
1. Il existe une méthode pour calculer mentalement le carré d’un nombre entier dont le chiffre des unités est 5.
Trouve le en regardant les nombres ci dessus.
2. Tu vas justifier !
k est un entier naturel dont le nombre des dizaines est a ( a appartient à N)
Par exemple, a = 13 pour 135.
On décompose k : k = a x 10 + 5
k = 10a +5
Prouve alors ce que tu as trouvé en mettant au carré !
Ton procédé fonctionne-t-il pour le produit de deux nombres entiers à 2 chiffres dont les chiffres des dizaines sont égaux et la somme des unités est 10 ?
Exercice 28 – Ordre et intervalles
1. Pour chaque ligne, reconstruire la phrase en utilisant Si……alors …. ou …si et seulement si ….:
a.
. Il pleut …….. .
. je prends mon parapluie.
I milieu de [AB] …….. .
. AI=BI
…….. .
.
…….. .
.
…….. .
. ABC est isocèle .
Exercice 29 :
Pour n entier naturel, comparer les nombres suivants :
Exercice 30 :
Pour ,comparer les nombres :
Exercice 31 – Intervalles
1. Compléter à l’aide des symboles
a.
b.
2. Préciser l’intervalle correspondant à :
a.
b.
c.
Exercice 32 – Ensemble de nombres
1. Calculer:
a.
b.
2. Simplifier puis donner sous forme d’écriture scientifique la fraction suivante :
3. Simplifier les écritures suivantes :
a.
b.
c.
3. Donner la décomposition en produit de facteurs premiers du nombre .
Exercice 33 :
a. Indiquer la nature des nombres suivants :
b. Simplifier l’écriture du nombre suivant :
Exercice 34 :
Mettre les nombres suivants sous forme irréductible , en détaillant les calculs
Exercice 35 :
Mettre les nombres suivants sous forme scientifique
Exercice 36 :
Calculez et simplifiez
Exercice 37 :
Au a) résoudre dans l’équation d’inconnue x . Rédiger soigneusement votre résolution.
Dans le b) exprimer y en fonction de x et préciser la valeur interdite pour x :
a) .
b)
Exercice 38 :
1. Donner l’intervalle représentant l’ensemble des réels x satisfaisant à la condition indiquée
a) b)
c) d)
2. Pour les deux cas suivants, représenter sur une droite graduée les intervalles I et J et donner leur intersection et leur réunion.
a) I = ]-∞ ; 4[ ; J = [1 ; 7]
b) I = ]-7 ; -3] ; J = ]-4 ; +∞[
Exercice 39 :
Effectuer les calculs suivants en respectant les priorités opératoires.
Exercice 40 :
Calculer puis simplifier au maximum le résultat.
Exercice 41 :
Ecrire sous la forme , où
et
sont deux entiers relatifs, avec b le plus petit possible.
Exercice 42 :
Développer et simplifier les expressions suivantes.
Exercice 43 :
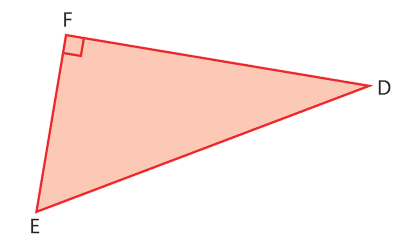
EDF est un triangle rectangle en F.
On donne cm et
cm.
1.Déterminer la valeur exacte de EF.
Donner le résultat sous la forme où
est un entier positif.
2. Donner la valeur exacte du périmètre du triangle EDF, puis l’arrondi au millimètre.
Exercice 44 :
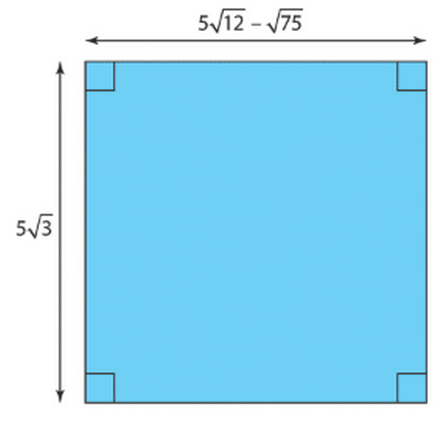
On considère la figure suivante. L’unité est le centimètre.
1.Ecrire sous la forme
, où
et
sont des entiers relatifs,
étant le plus petit possible.
2. Quelle est la nature exacte de ABCD ? Justifier
3. Déterminer le périmètre de ABCD sous la forme la plus simple possible.
Donner ensuite l’arrondi au millimètre.
4. Déterminer la valeur exacte de l’aire de ABCD.
Exercice 45 :
L’escalier d’une tour a un nombre de marches compris entre 130 et 150.
Si je les monte trois par trois, j’arrive en haut.
Si j’étais capable de les monter 4 par 4, je finirais par 1 marche.
Combien y a-t-il de marches ?
Exercice 46 :
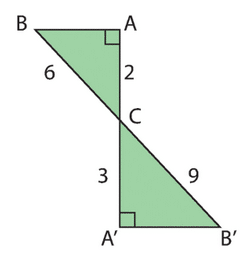
1. Calculer la valeur de .
2. En utilisant la définition d’une racine carrée, écrire le résultat
précédent sous la forme où a et b sont des entiers positifs, avec
.
3. Calculer AB puis AB’.
4. Comparer les deux écritures de et trouver un moyen pour simplifier
.
Exercice 47 :
Simplifier les écritures des nombres.
Exercice 48 :
a. Démontrer que pour tout entier naturel n non nul :
b. En déduire la valeur de la somme S définie par :
Exercice 49 :
Indiquez par une croix, l’appartenance des nombres de la première ligne aux ensembles indiqués
dans la première colonne :
| |
|
|
|
|
|
|
Exercice 50 :
Mettre les nombres suivants sous forme irréductible , en détaillant les calculs
Exercice 51 :
Mettre les nombres suivants sous la forme avec x
[1 ; 10[ et p
;
Exercice 52 :
Calculez et simplifiez
Exercice 53 :
Résoudre dans les équations suivantes d’inconnue x .
Rédiger soigneusement votre résolution.
Dans le b) on veillera à factoriser avant de résoudre :.
a)
b).
Exercice 54 :
1.Décomposer 204 et 595 en produits de facteurs premiers.
2.Simplifier la fraction .
Exercice 55 :
Recopier et compléter.
a) b)
c) d)
Exercice 56 :
Ecrire sous la forme , où
est un nombre relatif et
est un entier relatif.
a) b)
c)
d) e)
f)
Exercice 57 :
Effectuer les calculs suivants en détaillant les étapes et donner les résultats sous la
forme d’une fraction irréductible.
a) b)
c) d)
Exercice 58 :
Sans utiliser de calculatrice, transformer les expressions suivantes de façon à obtenir la racine carrée d’une fraction irréductible.
a) b)
c) d)
Exercice 59 :
Un fleuriste dispose de 30 tulipes et 24 muscaris.
Il veut composer des bouquets contenant le même nombre de tulipes et le même
nombre de muscaris, et utiliser toutes ses fleurs. On veut calculer le nombre maximum de bouquets qu’il peut faire.
1. Expliquer pourquoi le nombre de bouquets doit être un diviseur commun à 30 et 24.
2. Déterminer les diviseurs de 30 et 24.
3. Combien de bouquets peut-il réaliser au maximum ?
Quelle est alors la composition de chaque bouquet ?
Exercice 60 :
Dire si les affirmations suivantes sont vraies.
Exercice 61 :
Les affirmations suivantes sont-elles vraies ou fausses ?
Si la réponse est fausse, donner un contre-exemple.
Si la réponse est vraie, justifier la réponse.
a. Un nombre rationnel est toujours un nombre réel.
b. Un nombre rationnel est toujours un nombre décimal.
c. L’inverse d’un nombre décimal est toujours un nombre décimal.
d. Un nombre entier est toujours un nombre décimal.
e. Un nombre entier est toujours un nombre rationnel.
Exercice 62 :
Soient et
a. Calculer et
.
b. Calculer et
.
Exercice 63 :
Simplifier l’écriture de chaque nombre :
Exercice 64 :
a. Ecrire A sous la forme où a est un entier naturel :
b. Ecrire B sous la forme où a est un entier naturel :
Exercice 65 :
Ecrire sous la forme où a et b sont des entiers naturels et b est le plus petit entier naturel possible :
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «calculs et problèmes : exercices de maths en 2de corrigés en PDF.» au format PDF.
Ressources de seconde
Cours de seconde
D'autres cours et exercices à consulter
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.