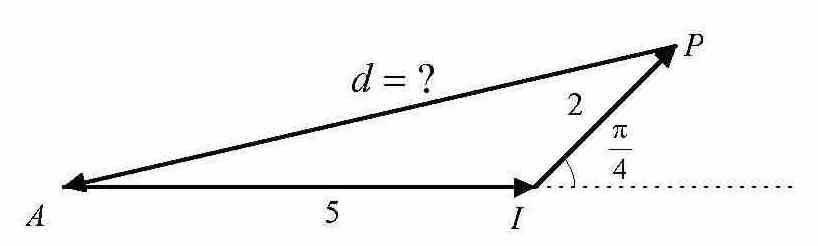Trigonométrie : exercices de maths en 1ère corrigés en PDF.

✏️Exercices

1ère • Lycée

Trigonométrie

⏱️ Temps de travail : 20-45 min

🎯 Niveau : Lycée

📱 Format : Gratuit

📄 PDF : Disponible

Des exercices de maths en 1ère corrigés sur les relations métriques dans le triangle quelconque.

Exercice 1 – Des équations trigonométriques
Résoudre dans les équations suivantes.
1.
2.

Exercice 2 – Déterminer la valeur de cosinus
Dans cet exercice, on donne :

Calculer la valeur exacte de puis de

Exercice 3 – Exercice sur la tangente
Dans cet exercice, on dispose de la donnée suivante :
1. Soit . Démontrer que
2. En déduire que :

Exercice 4 – Résoudre une équation trigonométrique
Résoudre dans l’équation : sin(2x) = cos(x).

Exercice 5 – Résoudre deux équations trigonométriques
Résoudre dans les équations suivantes :

Exercice 6 – Résoudre une équation trigonométrique complexe
Résoudre dans l’équation :

Exercice 7 – Triangle équilatéral et mesure d’angles
Sur la figure ci-dessous, ABC est équilatéral, BCI et ACJ sont rectangles isocèles respectivement en B et J.

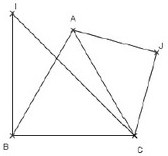
1. Déterminer une mesure de chacun des angles suivants :

2. Montrer que les points A,I et J sont alignés.

Exercice 8 – Cercle trigonométrique et points
Tracer un cercle trigonométrique et placer sur ce cercle
les points A, M, N, P et Q repérés par les nombres suivants :

Exercice 9 – Mesure principale d’un angle
Déterminer la mesure principale des angles :
$\alpha =\frac{114\pi}{4}$ ; $\beta =-\frac{91\pi}{6}$ ; $\gamma =70$

Exercice 10 – Relations métriques dans le triangle
ABC est un triangle avec .
1. Démontrer que $sin \, \widehat{A}=\frac{\sqrt{6}+\sqrt{2}}{4}$ .
2. Calculer les valeurs exactes de AB et AC .

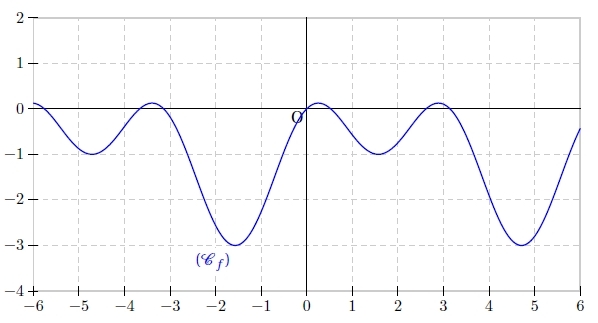
Exercice 11 – Représentation graphique de fonctions trigonométriques
Démontrer que la représentation graphique de la fonction définie sur par :

est située entre les droites d’équation y = – 3 et y = 1 .

Exercice 12 – Résoudre une équation trigonométrique
Démontrer que, pour tout réel :

Exercice 13 – Utiliser les formules d’addition
En utilisant les formules d’addition, calculer la valeur exacte de

Exercice 14 – Les formules d’Al-Kashi
Soit ABC un triangle quelconque.
On note :
– a la longueur du segment [BC] ;
– b la longueur du segment [AC] ;
– c la longueur du segment [AB] ;

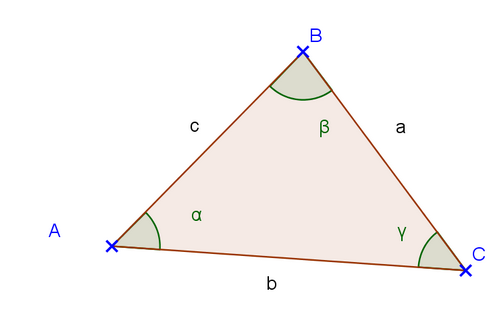
Montrer que :
$a^2=b^2+c^2-2bc\times cos(\alpha )\\b^2=a^2+c^2-2ac\times cos(\beta )\\c^2=a^2+b^2-2ab\times cos(\gamma )\\$

Exercice 15 -Formule de trigonométrie
Montre que :

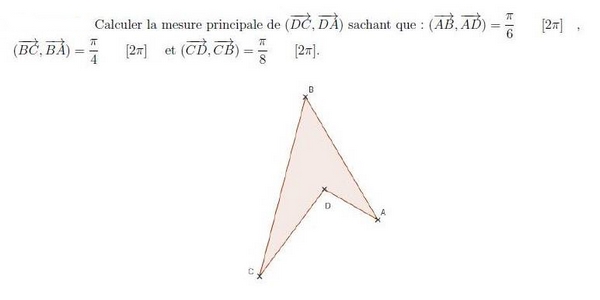
Exercice 16 -Mesure principale et figure dans le plan
Calculer la mesure principale de sachant que :

Exercice 17 -Relations métrique dans le triangle

ABC est un triangle avec BC = 4, et .
1. Démontrer que .
2. Calculer les valeurs exactes de AB et AC.
3. Calculer la valeur exacte de l’aire de ABC.

Exercice 18
Un triangle ABC a pour aire S = 5 cm².
De plus, c=AB=13 cm et b=AC= 2 cm.
Calculer la (ou les) longueur(s) possible(s) du troisième côté a = BC.

Exercice 19
ABC est un triangle .
On sait que AB = 7, AC= 4 et .
1. Calculer la valeur exacte de BC.
2. Calculer la valeur exacte de .

Exercice 20
Démontrer que deux angles supplémentaires ont le même sinus.
ABCD est un quadrilatère.On suppose que les segments [AC] et [BD] sont à l’intérieur du quadrilatère.
Démontrer que l’aire S du quadrilatère ABCD est donnée par :
( désigne l’angle formé par les diagonales).

Exercice 21
Un promeneur marche 5 km en direction de l’est, puis 2 km en direction du nord-est.Surpris par le mauvais temps, il retourne directement vers son point de départ en courant.
Sur quelle distance d a-t-il couru ?
On donnera la valeur exacte puis la valeur approchée à 0,01 km près.

Exercice 22
Démontrer la propriété suivante :
ABC est un triangle rectangle en A .

Exercice 23 :

Soit g la fonction définie sur $\mathbb{R}$ par :

1)Montrer que g est paire. Interpréter graphiquement.

2)Montrer que g est $\frac{\pi}{2}$ – périodique.

Exercice 24 :

soit g la fonction définie sur $\mathbb{R}$ par :

1)Montrer que g n’est ni paire ni impaire.

2)Montrer que g est $2\pi$ – périodique. Interpréter graphiquement.

3)Montrer que, pour tout réel , $-2\leq g(x)\leq 2$ .

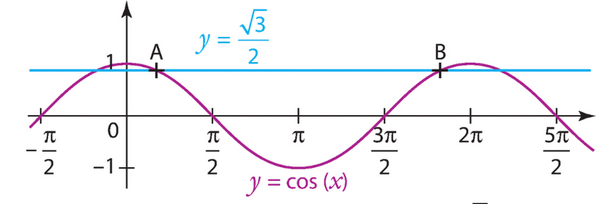
Exercice 25 :

1)A partir de $cos(\frac{\pi}{3})$ , déterminer $cos(-\frac{\pi}{3})$ puis $cos(\frac{2\pi}{3})$ .

2)Même question avec $sin(-\frac{\pi}{3})$ puis $sin(\frac{2\pi}{3})$ .

Exercice 26 :

1)Résoudre sur $[0;2\pi[$ l’équation $cos(x)=\frac{\sqrt{3}}{2}$ .

2)Résoudre sur $[0;2\pi[$ , l’équation $sin(x)=\frac{\sqrt{2}}{2}$ .

Exercice 27 :

1.Donner les abscisses des points A et B.

2)Résoudre sur $[0;2\pi[$ , l’équation $cos(x)=\frac{\sqrt{3}}{2}$ .

3)Résoudre sur $[0;2\pi[$ , l’inéquation $cos(x) \leq \frac{\sqrt{3}}{2}$ .

Exercice 28 :

Dans chaque cas, vérifier que la fonction f est T-périodique.

$a)f:x \mapsto cos(2\pi x)$ et T = 1.

$b)f:x \mapsto sin(3x)$ et $T=\frac{2\pi}{3}$ .

$c)f:x \mapsto \frac{2}{3}cos(7x+\frac{\pi}{4})$ et $T=\frac{2\pi}{7}$ .

$d)f:x \mapsto \frac{10}{7}sin(\frac{5x-8}{3})$ et $T=\frac{6\pi}{5}$ .

Exercice 29 :

1.a)Déterminer un réel x appartenant à l’intervalle $]-\pi;\pi[$ associé à $\frac{91\pi}{4}$ .

b)En déduire $cos(\frac{91\pi}{4})$ puis, $sin(\frac{91\pi}{4})$ .

2.a)Calculer $cos(-\frac{13\pi}{6})$ .

b)Calculer $sin(-\frac{81\pi}{2})$ .

3)a)Calculer $cos(\frac{25\pi}{3})$ et en déduire $sin(\frac{25\pi}{3})$ .

b)Calculer $sin(\frac{45\pi}{6})$ et en déduire $cos(\frac{45\pi}{6})$ .

Exercice 30 :

Soit f la fonction définie sur $]-\pi ; \pi ]$ par :

$f(x) = 4cos^2(x) + 2(\sqrt{2} - l)cos(x) -\sqrt{2}.$
Le but de l’exercice est de trouver les solutions de l’équation
f(x) = 0 et de l’inéquation f(x) > 0.
1. On pose X = cos(x).
a) Montrer que -1 <X< 1.
b) Montrer que résoudre l’équation f(x) = 0 revient à
résoudre l’équation $4X^2 + 2(\sqrt{2} - l)X -\sqrt{2}=0.$

c)Résoudre sur [- 1 ; 1], l’équation $4X^2 + 2(\sqrt{2} - l)X -\sqrt{2}=0.$
On notera et les solutions obtenues.
d) En déduire les solutions sur $]-\pi ; \pi ]$ de l’équation f(x) = 0.
2. On pose X = cos(x).
a) Résoudre sur [-1 ; 1] l’inéquation $4X^2 + 2(\sqrt{2} - l)X -\sqrt{2}>0.$

Exercice 31 :

1. Un disque microsillon tournant 33 tours et $\frac{1}{3}$ de tour par minute contient 6 chansons pour une durée
totale de 60 min. La durée de chaque chanson est la même.
Le Saphir situé l’extrémité du bras de lecture étant situé en N au début de la 1ère chanson, sur quel demi-axe se trouvera-t-il la fin de la chanson ?

2. Un disque microsillon tourne 16 tours et $\frac{2}{3}$ de tour par minute.

La durée de chaque chanson est égale 5 min.
Le saphir situé l’extrémité du bras de lecture étant situé en P au début de la 1ère chanson, sur quel demi-axe se trouvera-t-il :
a) au bout de 3 min ?
b) au bout de 4 min ?
c) à la fin de la 1ère chanson ?
d) à la fin de la 2ème chanson ?

Exercice 32 :

Soit f la fonction définie sur $\mathbb{R}$ par $f(x)=\frac{cos(x)}{3+sin^2(x)}$ .
1. Montrer que f est paire et $2\pi$ -périodique.

Interpréter graphiquement.
2. En déduire le plus petit intervalle I possible pour étudier f.
3. On admet que f est dérivable de dérivée :

$f'(x)=\frac{sin(x)(sin^2(x)-5)}{(3+sin^2(x))^2}$ .
a) En déduire les variations de la fonction f sur l.
b) Préciser les extrema locaux de f sur l.
c) Tracer la courbe représentative de f sur [- $\pi$ ; 3 $\pi$ ].

Exercice 33 :

Soit f la fonction définie sur $\mathbb{R}$ par $f (x) =-\frac{cos^3(x)}{3}$ .
1. Montrer que f est paire et $2\pi$ -périodique. Interpréter graphiquement.
2. On admet que la dérivée de la fonction f est la fonction $f'$ définie par :
$f'(x) = cos^2(x)sin(x)$ .

a) Étudier le signe de $f'(x)$ .
b) En déduire le sens de variation de la fonction f sur l’intervalle [0 ; $2\pi$ [.
c) Dresser le tableau de variations de la fonction f sur l’intervalle $[-\pi;3\pi[$ .

Exercice 34 :

On note (E) l’équation .
1.Montrer que les solutions de cette équation appartiennent l’intervalle [—1 ; 1].
2. Soit f la fonction définie sur l’intervalle [—1 ; 1] par f(x) = cos(x) + x.
a) Tracer f à l’aide de la calculatrice puis conjecturer le nombre de solutions de l’équation (E).
Justifier la démarche.
b) On admet que la dérivée de la fonction $x \mapsto cos(x)$ est la fonction $x \mapsto -sin(x)$ .

En déduire que $f'(x) = -sin(x) + 1$ .
c) Étudier le signe de $f'(x)$ et en déduire le sens de variation de la fonction f sur l’intervalle [—1 ; 1].
d) A l’aide de la calculatrice, donner une valeur approchée à 0,01 prés de la (ou les) solution(s).

Exercice 35 :

Les lentilles situées en haut de ce phare ont une portée lumineuse de 45 km et
une durée de rotation de 5 secondes.
1.Déterminer l’angle parcouru par une lentille en 1 seconde.
2. Calculer l’aire balayée par une lentille en 1 seconde.

Exercice 36 :

Soit m un paramètre réel non nul et la fonction définie sur $\mathbb{R}$ par .
1. Montrer que est paire. Interpréter graphiquement.
2. Montrer que est périodique de période $T=\frac{2\pi}{m}$ .
3. En déduire qu’on peut étudier sur l’intervalle $[0;\frac{\pi}{m}]$ .
4. On admet que est dérivable de dérivée :

$f'_m (x)=-msin(mx)$ . Selon m :
a) Déterminer le signe de $f'_m(x)$ sur l’intervalle $[0;\frac{\pi}{m}]$ .

b) En déduire les variations de sur l’intervalle $[0;\frac{\pi}{m}]$ .
c) Dresser le tableau de variations de sur l’intervalle $[0;\frac{\pi}{m}]$ puis sur l’intervalle $[-\frac{\pi}{m};\frac{2\pi}{m}]$ .

Exercice 37 :

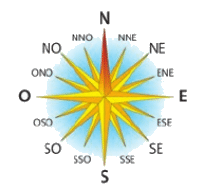
On considère la rose des vents ci-dessous.
On admet qu’un réel ayant pour image le sens « E » est 0 et qu’un réel ayant le sens « N » est $\frac{\pi}{2}$ .

1.Déterminer un réel ayant pour image le sens « O ».
2.Déterminer un réel ayant pour image le sens « S ».
3.Déterminer un réel ayant pour image le sens « NE ».
4.a) Déterminer un réel ayant pour image le sens « NNE »
b) Par symétrie, quel réel peut avoir pour image le sens « SSE» ?
c) Par symétrie, quel réel peut avoir pour image le sens « NNO » ?

Exercice 38 :

Calculer :

$A=cos(\frac{\pi}{4})+cos(\frac{3\pi}{4})$

$B=sin(\frac{\pi}{3})-cos(\frac{\pi}{4})+sin(\frac{5\pi}{3})$

$C=cos^2(\frac{\pi}{2})-sin^2(\frac{\pi}{2})$

Exercice 39 :

Calculer :

$D=-cos(\frac{7\pi}{3})+cos(\frac{41\pi}{3})$

$B=sin(-\frac{87\pi}{4}) +sin(-\frac{21\pi}{6})$

Exercice 40 :

Exercice 41 :

Soit f la fonction définie sur $\mathbb{R}$ par .

La courbe représentative de f passe par les points $M(-\frac{\pi}{2};2)$ et $N(\frac{\pi}{4};\sqrt{2})$ .

1.A l’aide des points M et N, déterminer les réels a et b.
2.En déduire l’expression de f en fonction de x.
3. Montrer que f est $2\pi$ -périodique. Interpréter graphiquement.

4. f est-elle paire ? impaire ? Justifier.

4.8/5 - (28849 votes)

Trigonométrie : exercices de maths en 1ère corrigés en PDF.

Probabilités : exercices de maths en 1ère corrigés en PDF.

Les suites : exercices de maths en 1ère corrigés en PDF.

Limites de fonctions : exercices de maths en 1ère corrigés en PDF.

Barycentre : exercices de maths en 1ère corrigés en PDF.

Les équations et inéquations du second degré : exercices de maths en 1ère corrigés en PDF.

Fonctions et variations : exercices de maths en 1ère corrigés en PDF.

Cours et exercices similaires :