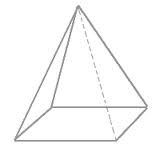
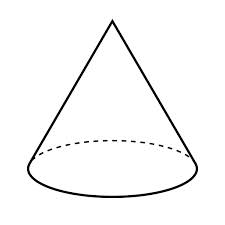
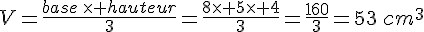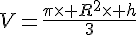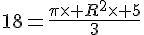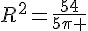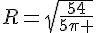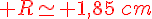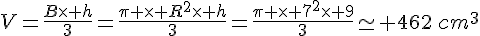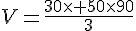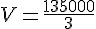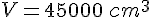Volume de pyramide et cône : corrigé des exercices de maths en 4ème en PDF.
Mis à jour le 13 septembre 2025
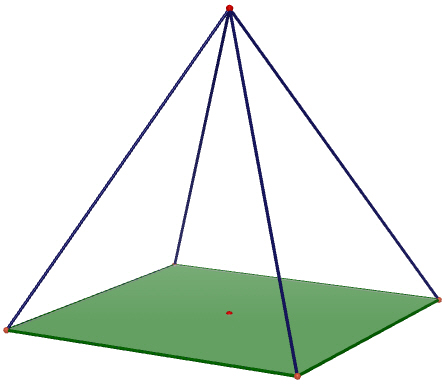
Exercice 1 :
Une pyramide a pour base un losange dont les diagonales ont pour dimensions 8 et 5 cm.
La hauteur de cette pyramide est de 4 cm.
Exercice 2 :
Convertir les volumes suivants en 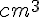 :
:
a. 6 dm3=6 000 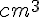 .
.
b. 0,9 daL=9 L=9 000 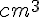 .
.
c. 45 mm3=0,045 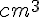 .
.
d. 0,092 m3 = 92 000 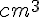
e. 0,039 hL=3,9 L=3 900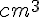 .
.
f. 0,000756 dam3 = 756 000 
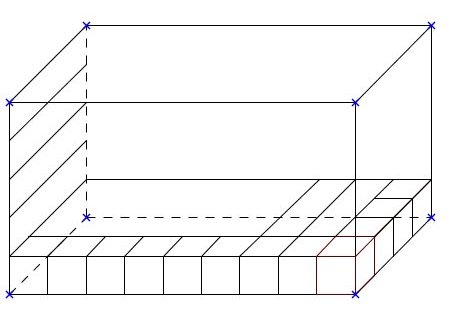
Exercice 3 :
Quelle est sa hauteur ?
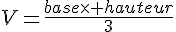
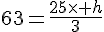
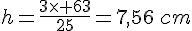
Conclusion : la hauteur de cette pyramide est de 7,56 cm.
Exercice 5 :
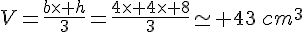
Exercice 7 :
Calculer son volume.
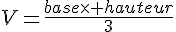
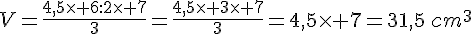
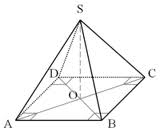
Exercice 9 :
Calculer son volume.
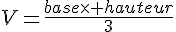
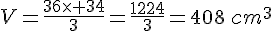
Conclusion :
Le volume de cette pyramide à base carrée est de 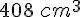 .
.
Exercice 10 :
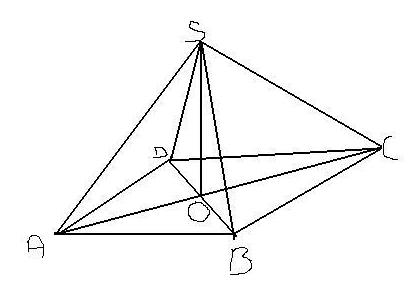
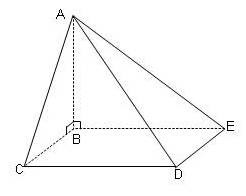
ABCDE est une pyramide droite à base rectangulaire.
- Quelle est la nature de BCDE ?
BCDE est un rectangle .
b. Quelle est la hauteur de ABCDE ?
La hauteur est [AB] .
c. On sait que AB = 5 cm, BC = 7 cm et BE = 9 cm.
Tracer en vraie grandeur le triangle ABC.
Calculer le volume de ABCDE.
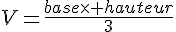
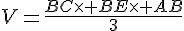
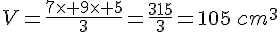
Exercice 11 :
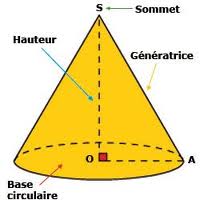
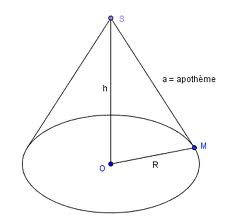
Voici un patron de cône de révolution.
1. Quel est le sommet de ce cône ?
Le point A
2. Quel est le centre et le rayon de son disque de base ?
Le point D et son rayon est de 1 cm .
3. Quelle est la longueur d’une génératrice ?
la longueur d’un génératrice est de 3 cm .
4. Calculer la longueur de l’arc de cercle BC.
C’est le périmètre du disque de base .
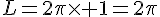
Exercice 16 :
Une pyramide a pour base un carré de 6 cm de côté et pour hauteur 34 cm. Calculer son volume.
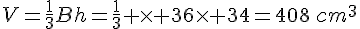
Exercice 17 :
Un cône a pour rayon de base 7cm, et pour hauteur 9cm. Calculer son volume, puis en donner une valeur approchée au centième de cm3 près.
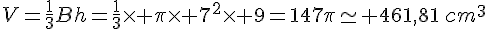
Exercice 18 :
Une pyramide a pour base un triangle ABC rectangle en B tel que AB = 4,5cm, AC = 7,5cm et BC = 6cm. Sa hauteur est de 7cm. Calculer son volume.
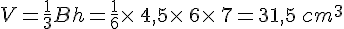
Exercice 19 :
Une pyramide a pour base un parallélogramme ABCD tel que AB = 4cm, AD = 4,5cm, et AH = 4cm (H est le point d’intersection de la perpendiculaire à (DC) passant par A). La hauteur de cette pyramide est de 8 cm. Calculer le volume de cette pyramide.
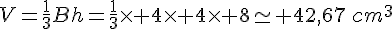
Exercice 20 :
Un cône a pour volume 18cm3. Sa hauteur est de 5cm. Quel est le rayon de son cercle de base ? (on donnera la valeur exacte, puis la valeur approchée au centième)
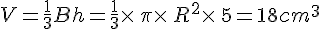
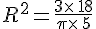 or R>0 donc
or R>0 donc
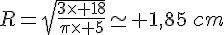
Exercice 21 :
Une pyramide a pour volume 63cm3, pour base un carré de 5cm de côté. Quelle est sa hauteur ?
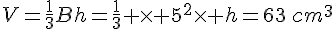
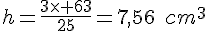
Exercice 22 :
Une pyramide a pour base un triangle DEF rectangle en E. On sait que sa hauteur (à la pyramide) est de 7cm, que DE = 4cm, et que son volume est de 0,05 L.
- Calculer EF.
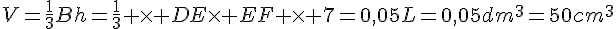
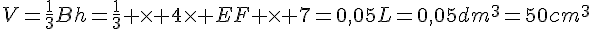
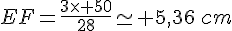
2.En déduire DF.
Le trangle DEF est rectangle en E donc d’après la partie directe du théorème de Pythagore :
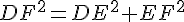
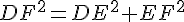
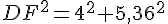
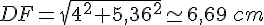
Exercice 23 :
Une pyramide a pour base un losange dont les diagonales mesurent respectivement 7 et 5 cm. Sa hauteur est de 12cm. Quel est son volume en dm3?
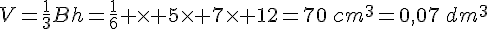
Exercice 24 :
Convertir les volume suivant en cm3 :
a. 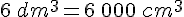 .
.
b. 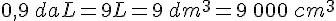 .
.
c. 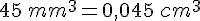 .
.
d. 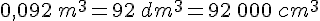 .
.
e. 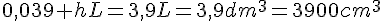 .
.
f. 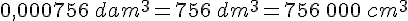
g. 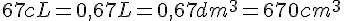 .
.
Exercice 25 :
Une pyramide a pour base un trapèze isocèle de hauteur 4cm, de petite base 5cm, de grande base 7cm. La hauteur de cette pyramide est de 14cm. Quel est son volume ?

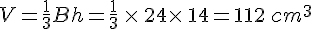
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «volume de pyramide et cône : corrigé des exercices de maths en 4ème en PDF.» au format PDF.
Ressources de quatrième
Cours de quatrième
Exercices de quatrième
D'autres cours et exercices à consulter
🤖 Exercices IA Interactifs ✨

Des milliers d'exercices interactifs conformes aux programmes officiels. Apprenez, pratiquez et progressez à votre rythme.
Exercices interactifsL'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.