Proportionnalité : exercices de maths en 4ème corrigés en PDF.
Mis à jour le 24 décembre 2025
Exercice 1 – Calcul de la quatrième proportionnelle
Dans les tableaux de proportionnalité, calculer en utilisant les produits en croix .
| 16 | 24 |
| 125 |
| 80 | 15 |
| 54 |
| 625 | |
| 42 | 12 |
Exercice 2 – Tableaux et produit en croix
Dans les tableaux de proportionnalité, calculer x en utilisant les produits en croix.
| 16 | 24 |
| 125 | x |
| 80 | 15 |
| 54 | x |
| 35 | x |
| 2100 | 10920 |
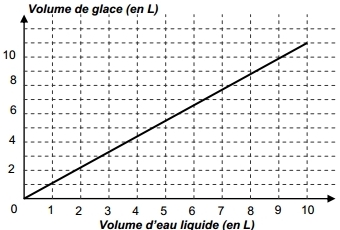
Exercice 3 – Volume d’eau
L’eau en gelant augmente de volume.
Le segment de droite ci-dessous représente le volume de glace (en litres) obtenu à partir d’un
volume d’eau liquide (en litres).
1. Quel est le volume de glace obtenu à partir de 6 litres de liquide ?
Laisse les traits de lecture (pointillés) en vert.
2. Quel volume d’eau liquide faut-il mettre à geler pour obtenir 10 litres de glace ?
Laisse les traits de lecture (pointillés) en rouge.
3. Le volume de glace est-il proportionnel au volume d’eau liquide ? Justifie sur ta copie.
Si c’est le cas, précise la valeur du coefficient de proportionnalité.
Exercice 4 – Problème du panda
Un panda mange 45,6 kg de bambous en 2 jours.
1. Quelle masse de bambous mange-t-il en 13 jours ?
2. Combien de jours lui faut-il pour manger 1 tonne de bambous ?
Arrondir le résultat à l’unité.
Rappel : 1 tonne = 1 000 kg .

Exercice 5 – Tube d’acier
Un tube d’acier de longueur 3,4 m a une masse de 41,7 kg.
1. Calculer la masse d’un tube de 5 m de cet acier (arrondir le résultat à l’unité) .
2. Un tube de cet acier a une masse de 8,34 kg .
Quelle est sa longueur ?

Exercice 6 – Vitesse moyenne d’un véhicule
Noah roule dans sa voiture à une vitesse de 2 m / s, alors
qu’Emma roule à une vitesse de 90 km / h .
Qui est le plus rapide ?
Exercice 7 – Vitesse moyenne et proportionnalité
Un objet se déplace à la vitesse de 100 m/s .
Cet objet se déplace à 36 km / h?à 360 km/h ? à 3600 km / h ?
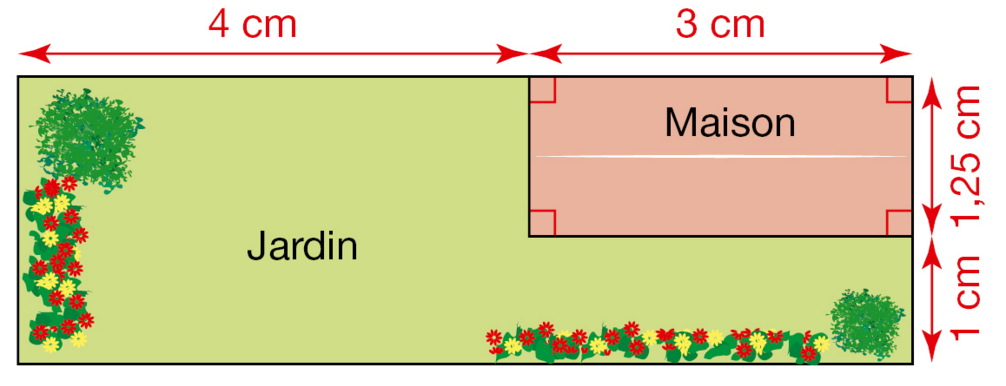
Exercice 8 – Mathématiques et environnement
Marion a installé une pompe pour arroser son jardin.
Cette pompe a un débit de 3 000 L par heure .
1. Combien de temps faudra-t-il à Marion pour remplir son arrosoir de 10 L .
2. Combien de temps faudra-t-il à Marion pour remplir sa citerne de 1 440 L ? Arrondir à l’unité.
3. Marion a fait fonctionner sa pompe pendant 12 min.
Quelle quantité d’eau a-t-elle utilisée ?
4. Si Marion oublie de fermer sa pompe pendant 2 jours,
quelle quantité d’eau aura-t-elle utilisée ?
Exercice 10 – Eclair et vitesse moyenne
Si je vois un éclair et si j’entends le tonnerre 8 s plus tard,
sachant que la vitesse du son est de 340 m/s , puis-je
savoir à quelle distance je me trouve de l’éclair .
Calculer cette distance .

Exercice 11 – Vitesse moyenne d’une girafe
Une girafe peut courir à la vitesse de 50 km / h .
1. a. Convertir 250 m en km .
b. Combien de temps met-elle pour parcourir 250 m à cette vitesse ?
2. Quelle distance parcourt-elle en 3 min à cette vitesse ?

Exercice 12 :
Voici les masses de deux lots de balles de tennis.
a. La masse est-elle proportionnelle au nombre de balles ?
b. Combien pèsent :
• 1 balle ? • 7 balles ?
c. Un lot de balles pèse 912 g.
Combien contient-il de balles ?
d. Pendant le Tournoi de Roland-Garros, on utilise environ 60 000 balles de tennis.
Calculer la masse de toutes ces balles : en kg, puis en tonnes.
Exercice 13 :
Dans chaque cas, dire si le tableau est un tableau de proportionnalité.
Justifier vos réponses.
Exercice 14 :
Voici des informations sur des boîtes.
a. Pour chaque affirmation ci-dessous, dire si elle est vraie ou fausse. Expliquer.
b. Calculer la masse de 11 de ces boîtes.
Exercice 15 :
Dans chaque cas, dire si la température est proportionnelle au temps et expliquer pourquoi.
Exercice 16 :
Afin de réduire les déchets d’emballages, une épicerie vend des produits au détail.
Carla a payé 3,90 € pour 1,2 kg de riz.
a. Quel est le prix de 1 kg ? de 4 kg ?
b. Calculer la quantité de riz achetée avec 6,50 €.

Exercice 17 :
Recopier et compléter le tableau de proportionnalité, en utilisant seulement la multiplication ou
l’addition de quantités.
Exercice 18 :
La masse de bois de sapin est proportionnelle à son volume.
a. Écrire l’égalité des produits en croix.
b. Calculer la valeur de x.
c. Faire une phrase pour interpréter le résultat.
Exercice 19 :
Le pied (ft) est une mesure de longueur anglosaxonne : 5 000 ft correspondent à 1 524 m.
a. Un ULM vole à 800 m d’altitude.
Convertir cette altitude en ft.
Donner une valeur approchée à l’unité près.
b. Pour les appareils qui effectuent « des vols à vue », la limite de survol de certaines
villes est fixée à 3 300 ft.
Convertir cette altitude en m.
c. Pour effectuer les calculs plus facilement, Noah utilise 30 cm comme correspondance pour 1 ft.
Quelle est la différence en cm, entre la mesure de Noah et la valeur exacte pour une longueur de 200 ft ?
Exercice 20 :
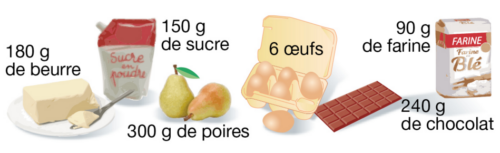
Valérie prépare un gâteau chocolat-poire à l’aide de la recette suivante :
Malheureusement, elle vient de faire tomber un oeuf et ne dispose plus que de 5 oeufs.
Aider Valérie à déterminer les nouvelles quantités des ingrédients.
Exercice 21 :
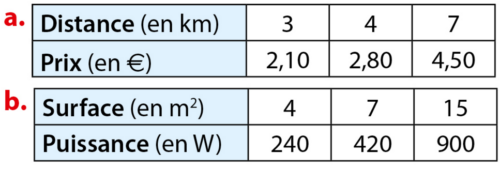
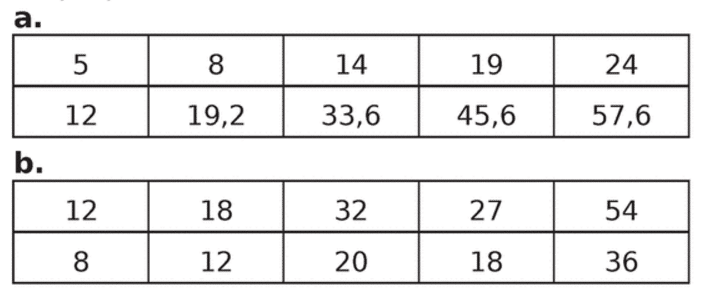
Les tableaux ci-dessous sont-ils des tableaux de proportionnalité ?
Exercice 22 :
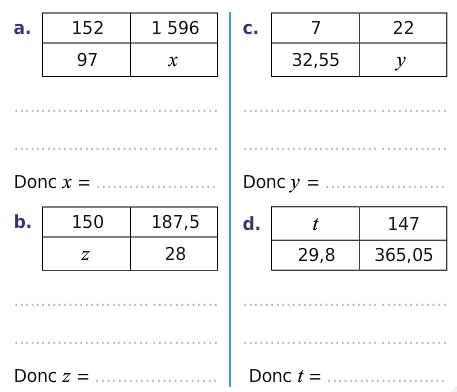
Pour chaque tableau de proportionnalité, calculer la valeur de la quatrième proportionnelle.
Exercice 23 :
-
- Une voiture roule à 85 km/h ; donner sa vitesse en mètres par seconde. (m/s)
- Le débit d’une rivière est 27
par seconde (
/s). Comment s ‘exprime ce débit en litres par minute ?
- Un cycliste parcourt 13 km en 16 min. Quelle est sa vitesse en km/h ?
Exercice 24 :
Une isolation thermique permet de réduire les frais de chauffage de 12%.
- Quelle était la dépense avant isolation si l’on paye après 4 254,80 €.
Exercice 25 :
Sur une carte de l’I.G.N. au 1/25 000, la distance d correspond à une distance D sur le terrain.
- Exprimer d en fonction de D , puis D en fonction de d.
- A quelle distance sur le terrain correspond une distance de 12 cm sur la carte ?
- A quelle distance sur la carte correspond une distance sur le terrain de 1,8 km ?
Exercice 26 :
La masse d’un mètre d’un certain fil de fer est de 30 g.
- Déterminer et représenter graphiquement la masse en fonction de la longueur du fil.
- Montrer comment sur ce graphique on peut lire la masse de 5 mètres de fil.
- Montrer comment sur ce graphique on peut lire la longueur d’un fil pesant 235 g.
Exercice 27 :
Une automobile consomme 6 litres d’essence pour parcourir 100 km à la vitesse de 90 km/h. On désigne par d la distance parcourue et par x la quantité d’essence utilisée.
- Calculer la consommation d’essence pour 1 km.
- Calculer la distance parcourue avec 1 litre d’essence.
- Représenter graphiquement la distance en fonction de la quantité d’essence utilisée.
- Montrer sur ce graphique la distance que l’on peut parcourir avec 14 litres.
- Montrer sur ce graphique la quantité d’essence nécessaire pour parcourir 420 km.
Exercice 28 :
Voici les masses de deux lots de balles de tennis.
a. La masse est-elle proportionnelle au nombre de balles ?
b. Combien pèsent :
•1 balle ?
• 7 balles ?
c. Un lot de balles pese 912 g.
Combien contient-il de balles ?
d. Pendant le Tournoi de Roland-Garros, on utilise environ 60 000 balles de tennis.
Calculer la masse de toutes ces balles : en kg, puis en tonnes.
Exercice 29 :
Voici des informations sur des boites.
a. Pour chaque affirmation ci-dessous, dire si elle est vraie ou fausse. Expliquer.
b. Calculer la masse de 11 de ces boîtes.
Exercice 30 :
Dans chaque cas, dire si le tableau est un tableau de proportionnalité.
Justifier vos réponses.
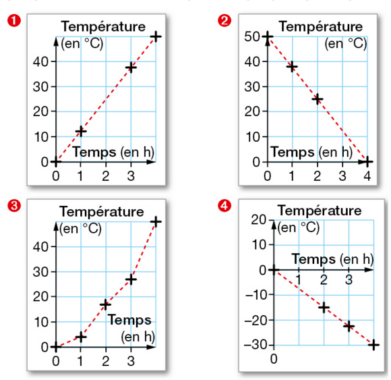
Exercice 31 :
Dans chaque cas, dire si la température est proportionnelle au temps et expliquer pourquoi.
Exercice 32 :
Gaspard effectue des travaux de jardinage. II est payé å l’heure.
Cette semaine, pour 20 h de travail, il a gagné 213 €.

a. Combien est-il payé pour 1 h de travail ?
b. La semaine prochaine, il prévoit de travailler 1 7 h.
Quelle somme d’argent va-t-il gagner ?
c. La semaine dernière, il a gagné 138,45 €.
Pendant combien d’heures a-t-il travaillé ?
Exercice 33 :
La masse de bois de sapin est proportionnelle son volume.
a. Ecrire l’égalité des produits en croix.
b. Calculer la valeur de x.
c. Rédiger une phrase pour interpréter le résultat.

Exercice 34 :
Pour imprimer des journaux, on utilise des rouleaux de papier.
a. Écrire l’égalité des produits en croix.
b. Calculer la valeur de .
c. Rédiger une phrase pour interpréter le résultat.
Exercice 35 :
Le pied (ft) est une mesure de longueur anglosaxonne : 5 000 ft correspondent à 1 524 m.
a. Un ULM vole à 800 m d’altitude.
Convertir cette altitude en ft.
Donner une valeur approchée à l’unité près.
b. Pour les appareils qui effectuent « des vols vue », la limite de survol de certaines
villes est fixée à 3 300 ft.
Convertir cette altitude en m.
c. Pour effectuer les calculs plus facilement, Noah utilise 30 cm comme correspondance pour 1 ft.
Quelle est la différence en cm, entre la mesure de Noah et la valeur exacte pour une longueur de 200 ft ?

Exercice 36 :
Valérie prépare un gâteau chocolat-poire à l’aide de la recette suivante :
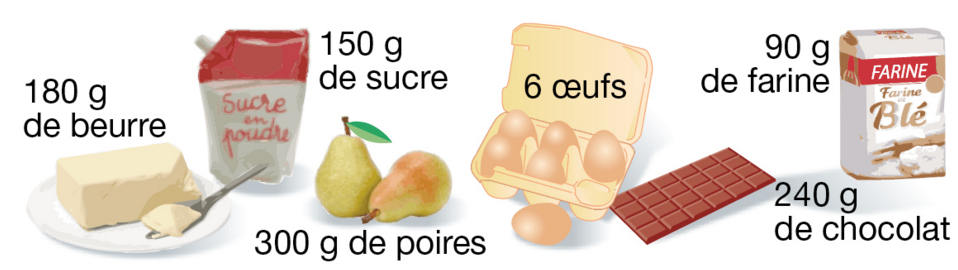
Malheureusement, elle vient de faire tomber un oeuf et ne dispose plus que de 5 oeufs.
Aider Valérie à déterminer les nouvelles quantités des ingrédients.
Exercice 37 :
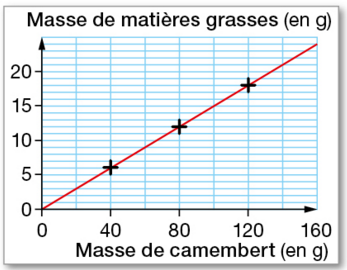
Le graphique ci-dessous représente la masse de matières grasses contenues dans un camembert allégé.
a. S’agit-il d’une situation de proportionnalité ?
Expliquer la réponse.
b. Quelle portion maximale de ce camembert peut-on consommer pour ne pas dépasser 6 g de matières
grasses ?
c. Quel est le pourcentage de matières grasses de ce camembert allégé ?
d. Calculer la masse de matières grasses contenue dans un camembert de 240 g.
Exercice 38 :
Pendant les soldes, une boutique Offre une remise de 20 % sur le prix des trois articles suivants :

a. Calculer le prix de la veste après la réduction.
b. Axel possède 150 €.
Peut-il acheter ces trois articles après la réduction ?
Sinon, lesquels peut-il acheter ?
Exercice 39 :
Voici les résultats obtenus par un candidat une élection dans deux bureaux de vote.

Quel pourcentage des bulletins exprimés a obtenu ce candidat dans l’ensemble des deux bureaux de vote ?
Exercice 40 :
Une maquette de la tour de Pise å l’échelle a une hauteur de 22,4 cm.
Quelle est la hauteur de cette tour sur une maquette à l’échelle ?
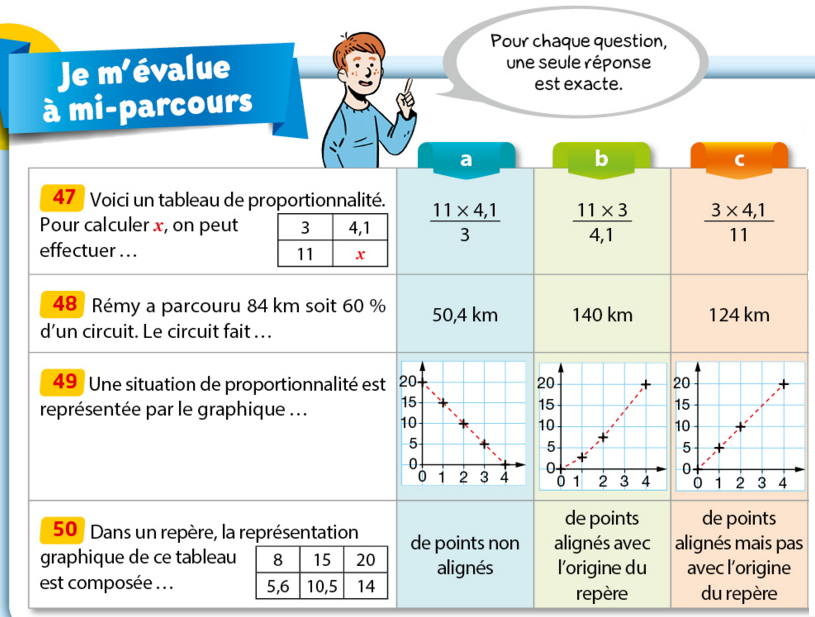
Exercice 41 :
Répondre à ce QCM sur la proportionnalité.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «proportionnalité : exercices de maths en 4ème corrigés en PDF.» au format PDF.
Ressources de quatrième
Cours de quatrième
Exercices de quatrième
D'autres cours et exercices à consulter
🤖 Exercices IA Interactifs ✨

Des milliers d'exercices interactifs conformes aux programmes officiels. Apprenez, pratiquez et progressez à votre rythme.
Exercices interactifsL'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.