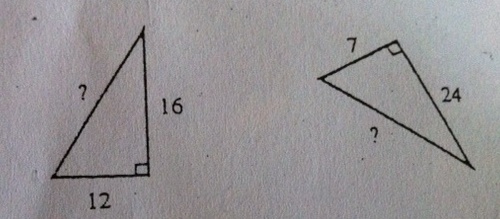Théorème de Pythagore : exercices de maths en 4ème corrigés en PDF.
Mis à jour le 15 août 2025
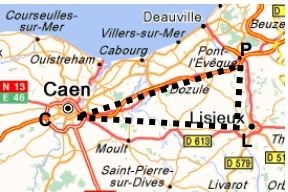
Exercice 1 – Carte géographique.
Sur une carte, le triangle CLP formé par les villes de Caen, Lisieux et Pont-l‘Evêque est considéré comme étant rectangle en L.
On donne : CP = 46 km et PL = 17 km.
1. Montre par le calcul que la distance CL est d’environ 43 km.
2. En mesurant CP sur la carte, on trouve 4,6 cm.
Retrouve l’échelle de la carte fournie.
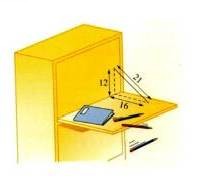
Exercice 2 – Secrétaire.
Mathieu est perplexe…
Ses parents lui ont acheté un secrétaire,
mais ses stylos roulent et tombent.
Peux-tu lui expliquer pourquoi ?
Exercice 3 – Longueur de câble.
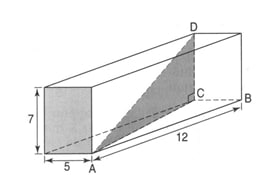
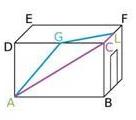
Une pièce d’une maison a la forme d’un pavé droit dont les dimensions sont AB = 5 m; BC = 2,5 m et DE = 4 m.
Un bricoleur doit amener un câble du point A au point L, milieu de [CF].
Il hésite entre les deux possibilités marquées en couleur sur la figure sachant que G est le milieu de [DC].
En bleu, de A vers G puis de G vers L.
En violet, de A vers C puis de C vers L.
a. Dans lequel des deux cas utilisera-t-il le moins de câble ?Justifier.
b. Construire sur une même figure, à l’échelle 1/100, les faces ABCD et CDEF.
Représenter les deux possibilités pour le passage du câble.
c. Le bricoleur veut utiliser le moins de câble possible.
Sur la figure suivante, représenter le passage du câble de longueur minimum.
Justifier votre tracé et calculer cette longueur.
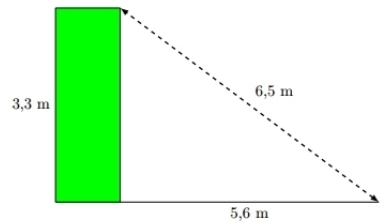
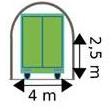
Exercice 4 – Le tunnel et le camion.
Un tunnel, à sens unique, d’une largeur de 4 m est constitué de deux parois verticales de 2,5 m de haut,
surmontées d’une voûte semi-circulaire de 4 m de diamètre.
Un camion de 2,6 m de large doit le traverser.
Quelle peut être la hauteur maximale de ce camion ?
Exercice 5 – Envoi d’une lettre par la poste.
Jean doit envoyer une lettre par la poste.
Peut-il envoyer cette lettre rectangulaire sans la plier ?

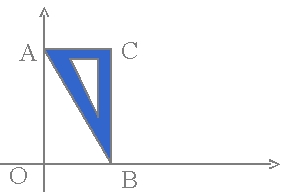
Exercice 6 – Problème ouvert de l’équerre.
Une équerre ABC est positionnée de telle sorte que
le point A est situé sur l’axe des ordonnées
et le point B sur celui de l’axe des abscisses.
On déplace l’équerre en faisant glisser les points A et B sur les axes.
Quelle est la trajectoire du point C ?
Exercice 7 – Spectacle de magie : le souci du magicien.
Pour son spectacle, un magicien veut enfoncer des épées dans une boîte dans laquelle serait enfermé un spectateur.
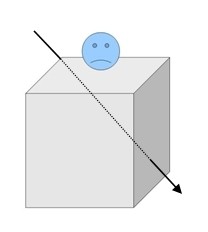
La boîte est un cube de 1m de côté.
Pour son projet, le magicien doit faire fabriquer des épées.
Il lui faut des épées toutes de même taille telles que, quel que soit l’endroit où il enfonce l’épée, elle puisse dépasser d’au moins 10 cm.
Quelle longueur minimum de lame d’épée doit-il commander au forgeron ?
Exercice 8 – Construire un troisième carré : problème ouvert.
Construire un troisième carré tel que celui-ci ait pour aire la somme des aires des deux carrés ci-dessous :
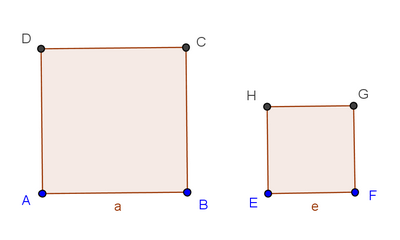
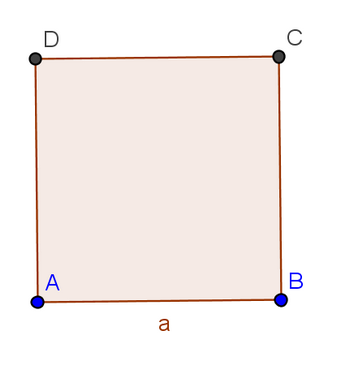
Exercice 9 – Calcul de l’aire d’un carré.
A partir du carré ci-dessous, vous devez construire un autre carré tel que celui-ci ait comme aire le double de celle du carré
ci-dessous .
Détaillez votre méthode.
Exercice 10 – Garage.
On accède au garage situé au sous-sol d’une maison par une rampe [AC].
On sait que : AC = l0,25 m ; BC = 2,25 m.
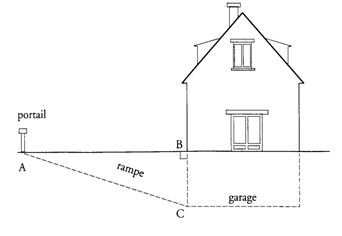
Calculer la distance AB entre le portail et l’entrée.
Exercice 11 – Vérifier que le triangle est rectangle.
On considère le schéma ci-contre (ne pas le reproduire).
a) Calculer AC et AE.
b) En déduire que le point A appartient à la médiatrice du segment [CE].
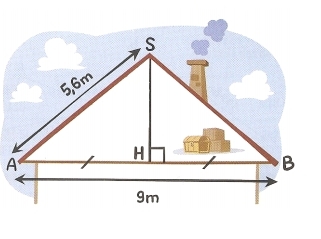
Voici le schéma d’une haie « à la française ».
Le jardinier a-t-il taillé une haie perpendiculaire au sol ?
Calculer la hauteur SH de ce grenier au dixième de mètre près.
Le bracelet de Zoé a douze perles espacées régulièrement sur une chaînette.
Zoé prétend qu’en tendant la chaîne entre des perles bien choisies, elle peut former un triangle rectangle.
Dessiner la chaîne dans une position qui lui permette d’obtenir un angle droit.
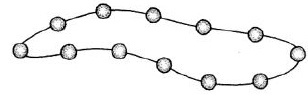
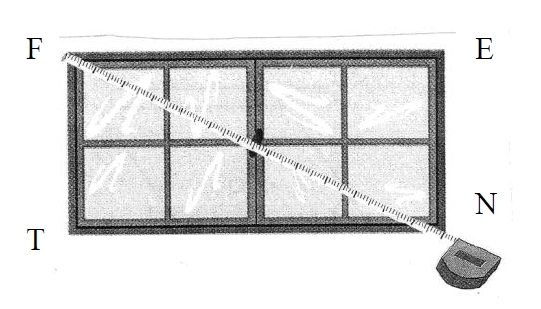
Exercice 16 – Fenêtre rectangulaire.
Un menuisier a construit un quadrilatère comme encadrement de fenêtre.
Deux côtés mesurent 60 cm et les deux autres mesurent 144 cm.
Il mesure la diagonale et trouve 156 cm.
La fenêtre est-elle bien rectangulaire ? Justifier votre réponse.
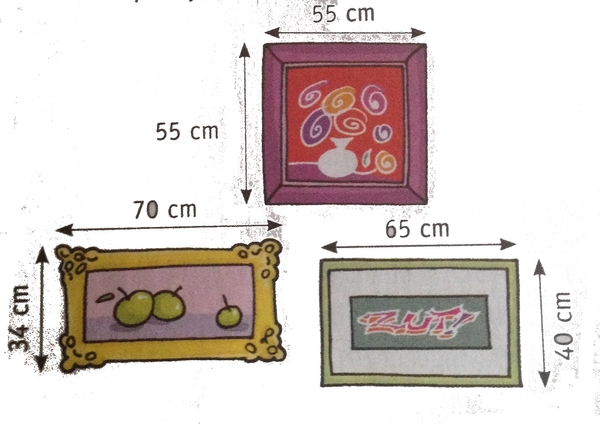
Exercice 17 – Carton de déménagement et tableaux.
Un carton de déménagement a pour dimensions :
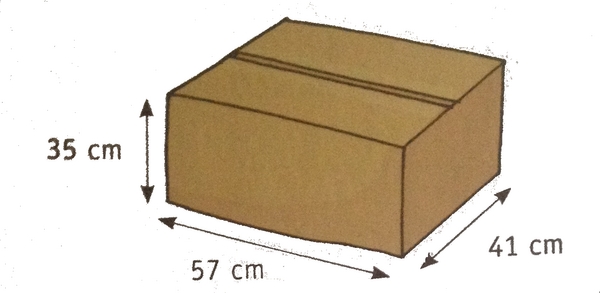
Un seul des trois tableaux suivants ne peut pas tenir dans ce carton.
Lequel? Justifier la réponse.
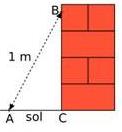
Exercice 18 – Construction d’un mur.
Pour apprendre son métier, un apprenti maçon a monté un mur en briques de 0,90 m de hauteur.
Son patron arrive pour vérifier son travail : il marque un point B sur le mur à 80 cm du sol et un point A à 60 cm du pied du mur.
Il mesure alors la distance entre les points A et B et il obtient 1 m.
L’apprenti a-t-il bien construit son mur perpendiculaire au sol ?Justifier.
Exercice 19 – Le collier de Clémence.
Clémence possède un collier qui contient 12 perles espacées régulièrement.
Elle affirme pouvoir vérifier à l’aide de son collier qu’un triangle est rectangle.
Pour cela, elle a besoin de former un triangle et de tendre son collier.
Elle numérote ses perles de 1 à 12.
a. Dessiner le collier de Clémence dans une position qui lui permet d’obtenir un angle droit.
b. Expliquer et justifier votre choix.

Exercice 20 – Fleurs sur une étagère.
Sur un mur vertical, Arnaud a installé une étagère pour y poser des pots de fleurs.
Les mesures qu’il a utilisées sont les suivantes :
AT = 42 cm; AE = 58 cm et TE = 40 cm.
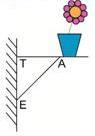
L’étagère d’Arnaud est-elle horizontale ?Justifier.
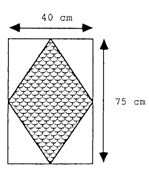
Exercice 21 – Le panneau d’une porte d’immeuble
Un panneau d’une porte d’immeuble mesure 75 cm sur 40 cm.
Il est décoré d’un losange en relief obtenu en joignant les milieux des côtés du panneau.
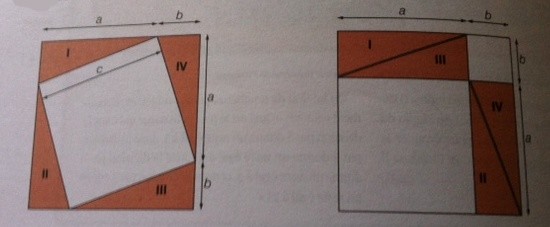
Ces deux mêmes tapis carrés ont été décorés à l’aide de quatre triangles rectangles identiques.
a. Quel est le motif qui nécessite le plus de laine blanche ?
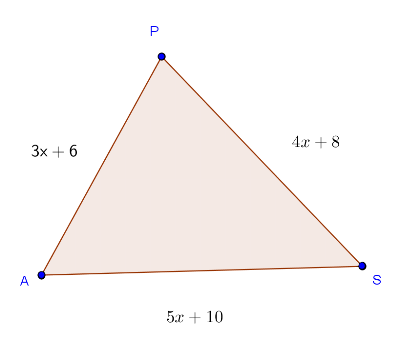
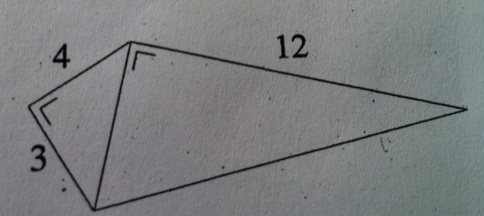
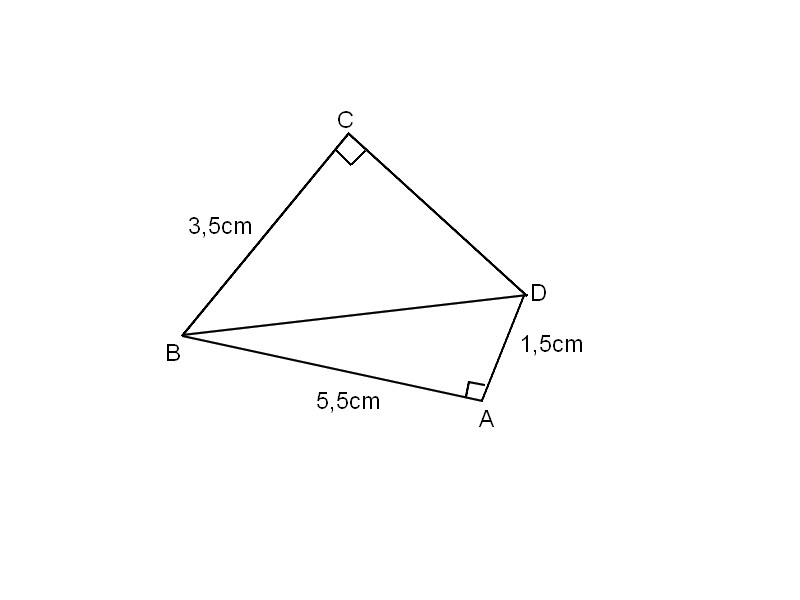
Exercice 25 – Quadrilatère convexe.
Voici le croquis d’un quadrilatère convexe.
1. Calculer les longueurs manquantes.
2. Calculer son aire.
Exercice 26 – Calculs de longueurs.
Dans chacun des cas suivants, calculer la longueur manquante.
Exercice 27 – Partie directe du théorème de Pythagore.
Soit ABC un triangle rectangle en A tel que AB=5 cm et AC=12 cm.
1.
a. Utiliser le théorème de Pythagore pour calculer la valeur exacte de la longueur BC de l’hypoténuse.
b. Construire le triangle ABC.
Vérifier votre calcul précédent en mesurant BC.
Exercice 28 – Calculer la longueur d’un côté
IJK est un triangle rectangle en I tel que IJ=4,5 cm et JK=7,5 cm.
Utiliser le théorème de Pythagore pour calculer la valeur exacte de la longueur IK.
Exercice 29 – Réciproque du théorème.
Dans chaque cas, dire si le triangle ABC est rectangle.
Si oui, préciser en quel point.
a. AB = 24 cm , AC = 7 cm, BC = 25 cm
b. AB = 4 cm, AC = 7 cm, BC = 5,75 cm.
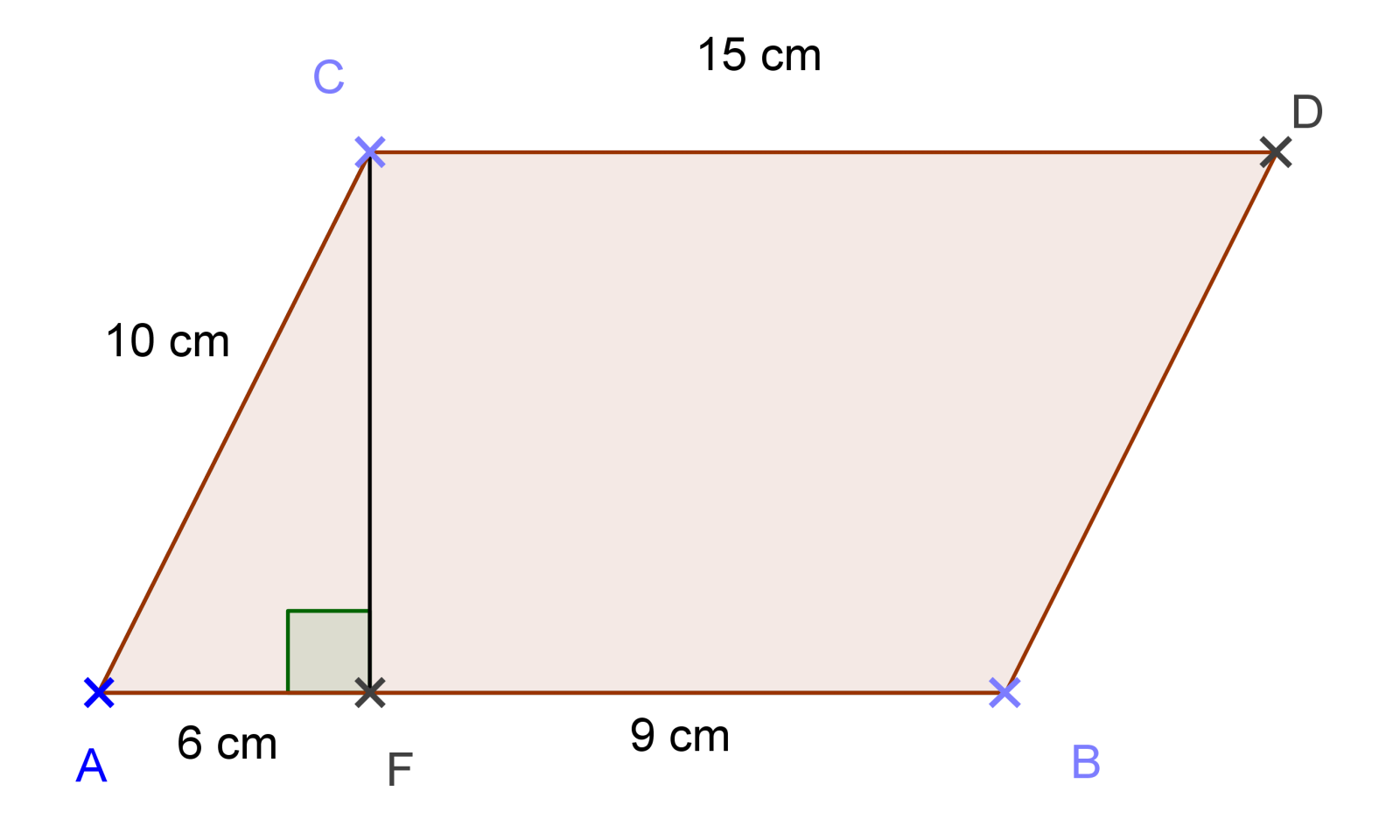
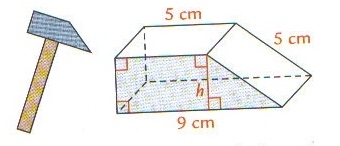
Exercice 30 – Etude d’un marteau.
La tête d’un marteau a la forme d’un prisme droit représenté sur la figure ci-dessous.
La base de ce prisme est le trapèze rectangle colorié ci-dessous.
Tracer ce trapèze à main levée et calculer sa hauteur h.
Exercice 31 – Etude d’un parallélépipède rectangle.
La figure ci-dessous représente un parallélépipède rectangle de longueur 1,2 mètres, de largeur 90 cm et de hauteur 50 cm.
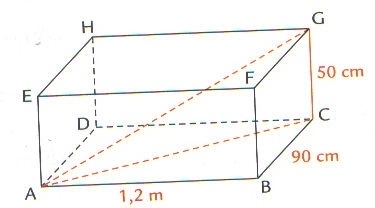
a. Quelle est la nature de la face ABCD ?
b. Calculer la longueur AC.
c. Quelle est la nature du triangle ACG ?
d. Calculer la longueur AG, arrondie au dixième, d’une diagonale du parallélépipède rectangle.
Exercice 32 – Etude d’un téléviseur
Monsieur Mathovore vient d’acheter un téléviseur de 56 cm.
A main levée, l’écran de ce téléviseur peut être représenté par le rectangle suivant :
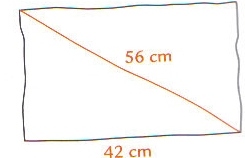
Quelle devra être la hauteur minimale du meuble de Monsieur Mathovore afin qu’il puisse y loger son téléviseur ?
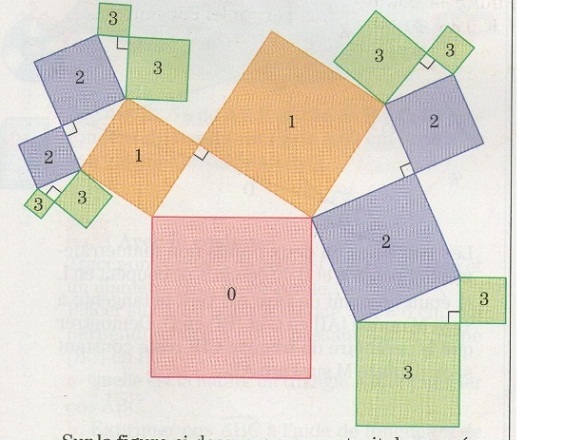
Exercice 33 – L’arbre de Pythagore
Sur la figure, on a construit des carrés et des triangles rectangles qui ont des côtés communs. Exprimer la somme des aires des carrés verts en fonction de l’aire du carré rose.
Exercice 34 – Cercle.
Tracer un cercle C dont un diamètre [AB] mesure 12cm. Sur ce cercle, placer un point C, tel que AC=8cm.
1)Nature de ABC ?
2)Calculer BC (valeur exacte simplifiée).
Sur la demi-droite [AC), placer le point D, tel que CD=10cm.
3)Calculer la longueur BD (valeur exacte simplifiée)
4)a. Combien mesurent les côtés du triangle ABD ?
b. Démontrer que ABD est rectangle.
5)Que peut-on dire de la droite (AD) pour le cercle?
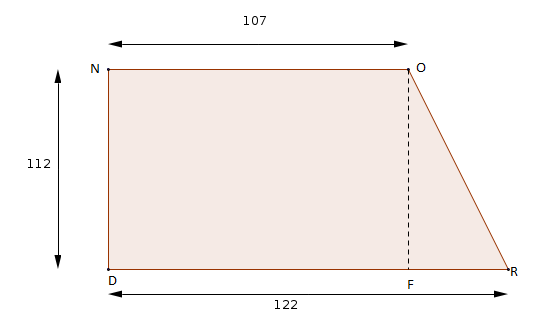
Exercice 35 – Le trapèze rectangle.
1 ) Quelle est la nature du quadrilatère NORD ?
2) Quelle est la nature du quadrilatère NOFD.
3) En déduire les longueurs FO , DF et FR.
4) Calculer la longueur OR.
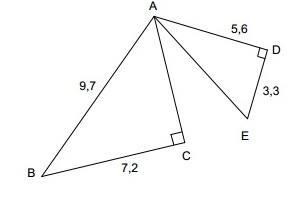
Exercice 36 – Applications.
On considère les deux triangles rectangles ci-dessous :
Calculer BD² puis CD .
Exercice 37 – Est-ce un triangle rectangle ?
Soit ABC, un triangle rectangle en B tel que AB = 6 cm et BC = 8 cm. Calculer la longueur AC.
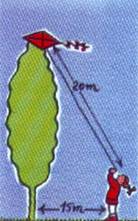
Exercice 38 – Cerf-volant.
Le cerf-volant de Maud s’est accroché à la cime d’un peuplier.
Maud sait que le fil de son cerf-volant mesure 20 m. Elle est à environ 15 m de l’arbre.
Sachant que Maud mesure 1,40 m
Quelle est donc approximativement la hauteur du peuplier ?
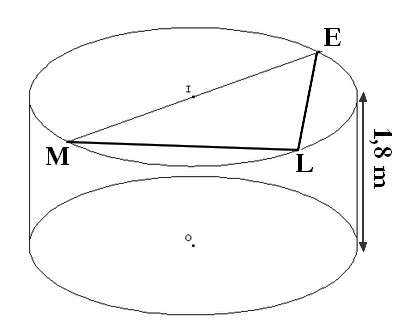
Exercice 39 – Problème ouvert de la piscine et cercle circonscrit
Mathys (M) et Ethan (M) sont assis en deux points diamétralement opposés
d’une piscine circulaire de profondeur 1,80 m .
Lorsque Louna (L) prend place au bord du même bassin, tous deux nagent tout droit vers elle.
Après un parcours de 10m, Mathys a déjà atteint Louna alors qu’Ethan devra nager 14m de plus que Mathys pour la rejoindre.
Combien de litre d’eau y a-t-il dans la piscine ? Expliquer .
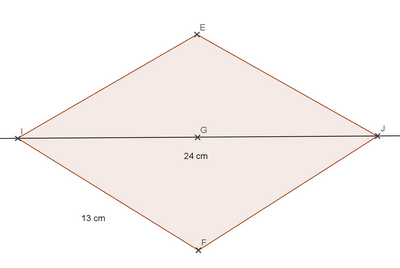
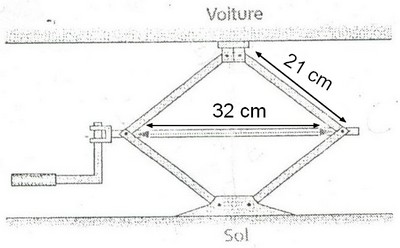
Exercice 40 – Le cric hydraulique pour automobile.
Le cric d’une voiture a la forme d’un losange de 21 cm de côté.
A quelle hauteur soulève-t-il la voiture lorsque la diagonale
horizontale mesure 32 cm ?
Exercice 41 – Problème ouvert sur le théorème de Pythagore.
ABC est un triangle rectangle en B tel que
AB = 4 cm et AC = 6,5 cm .
Calculer BC .
.png)
Exercice 42 – Calculs d’aires
ABCD est un rectangle et l’unité est le centimètre.
DKC est un triangle rectangle en K .
BC = 12 cm , DK = 24 cm et KC = 7 cm.
Calculer l’aire noire.

Exercice 43 – Réciproque du théorème de Pythagore et application
Dans chaque cas, démontrer que le triangle ABC est rectangle et préciser son hypoténuse.
Les longueurs données sont en mm.
Triangle 1 :
AB = 22,1 AC = 14 et BC = 17,1
Triangle 2 :
AB = 60 AC= 100 et BC = 80.
Exercice 44 – Réciproque.
Le triangle suivant AB=7,3 cm ; AC = 5,5 cm et BC = 4,8 cm est -il rectangle ?
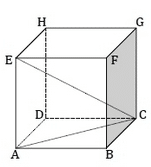
Exercice 45 – Volume d’un cube
ABCDEFGH est un cube d’ arête 4 cm.
1. Quelle est la nature de la face ABCD ?
2. Quelle est la nature du triangle ABC ?
3.Que représente le segment [AC] pour la face ABCD ?
4. Que représente le segment [AC] pour le triangle ABC ?
5. Quelle est la nature du triangle ACE ?
6. Que représente le segment [CE] pour le triangle ACE ?
7. Calculer la longueur AC au millimètre près.
8) Utiliser la valeur de pour calculer la valeur exacte de la longueur CE.
Donner l’arrondi, au millimètre prés, de la longueur CE.
Donner ensuite leurs valeurs approchées au millième.
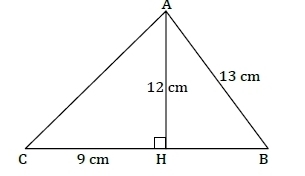
Exercice 47 :
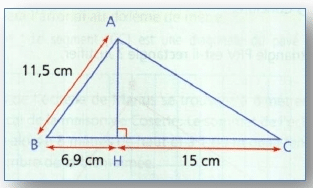
1. A l’aide des informations données par la figure, calculer AC et HB.
2. Calculer l’aire et le périmètre du triangle ABC.
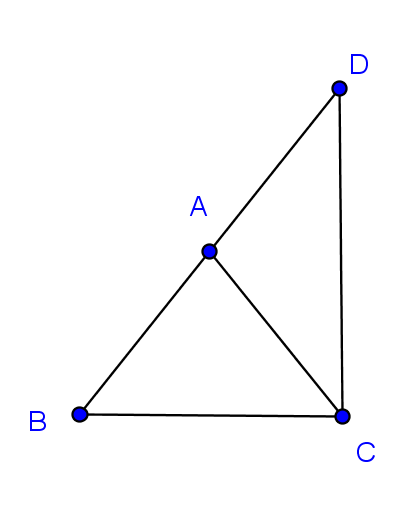
Exercice 48 :
– ABC est un triangle isocèle en A.
– D est le symétrique de B par rapport à A.
Démontrer que le triangle BCD est un triangle rectangle.
Exercice 49 :
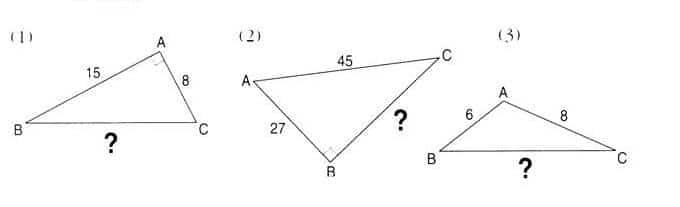
1) Dans chacun des cas suivants, calculer, si possible, la longueur BC.
Toutes les longueurs sont données en centimètres.
2) RST est un triangle rectangle en R tel que RS = 2 cm et RT = 1 cm. Calculer ST.
Le résultat en centimètres est-il un nombre entier ? Sinon, trouver un arrondi de ST au dixième de centimètre près.
Exercice 50 :
Qui a raison ?
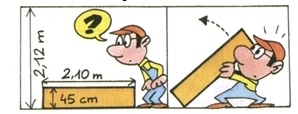
Exercice 51 : La surprise finale
Le plafond est-il assez haut pour que Monsieur Bricoltou mette en place son meuble ?
Exercice 52 :
Une chèvre C est attachée à un piquet P planté au coin d’un pré carré de 15 m de côté.
Quelle doit être, approximativement, la longueur de la corde pour que la chèvre puisse brouter tout le pré?
Exercice 53 : Le parallélépipède rectangle
Combien mesure à 0,01 près, la diagonale du parallélépipède rectangle?
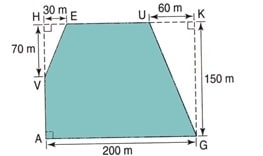
Exercice 54 :
Monsieur Crésus possède un terrain VAGUE qu’il veut clôturer.
Calculer le périmètre du terrain VAGUE.
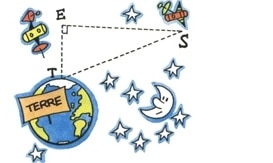
Exercice 55 :
Quelle distance sépare les deux satellites E et S, sachant que l’angle est droit et qu’un signal radio met
de seconde de S à T et
de seconde de E à T ?
(Vitesse du signal radio : 300 000 km/s.)
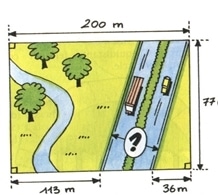
Exercice 56 :
Quelle est la largeur de l’autoroute ?
(Non, ce n’est pas 51 mètres !)
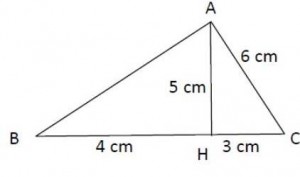
Exercice 57 : la hauteur d’un triangle
La droite (AH) est-elle une hauteur du triangle ABC ?
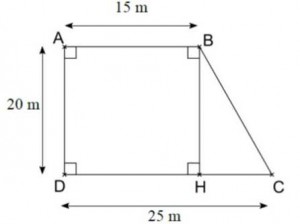
Exercice 58 : la clôture d’un jardin
Monsieur Maud achète 80 mètres de grillage pour clôturer son jardin dont la forme et les dimensions sont données par la figure ci-dessous :
Aura-t-il assez de grillage ?
Justifier la réponse.
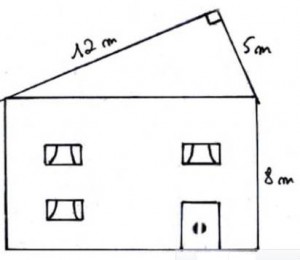
Exercice 59 :la façade d’une grande case de St-Pierre
La figure ci-contre représente la façade d’une grande case de St-Pierre.
Les trois fenêtres ont la même dimension (2.00 m x 1.00m)
La porte mesure 2.00 m x 2.40 m
Une entreprise se charge de peindre cette façade.
Un bidon de peinture de 10 L coûte 75 € et permet de couvrir une surface de 50 m².
On souhaite passer 2 couches de peinture sur la façade de cette case. Calculer le nombre de bidons nécessaires ainsi que le coût de la peinture.
Dans cet exercice, toute trace de recherche, même non aboutie, sera prise en compte dans l’évaluation.
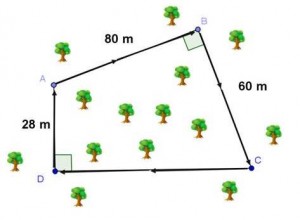
Exercice 60 : le parcours d’endurance du CROSS du collège
Voici une représentation du parcours d’endurance des élèves d’une classe de 4°.
Ils doivent parcourir une distance de 1,4 km en partant du point A et en suivant le sens des flèches.
Où doivent-ils arriver ?
Exercice 61 :
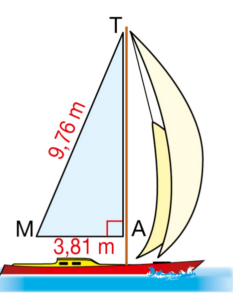
La voile MAT de ce bateau peut être assimilée un triangle rectangle en A, tel que :
AM = 3,81 m et TM = 9,76 m.
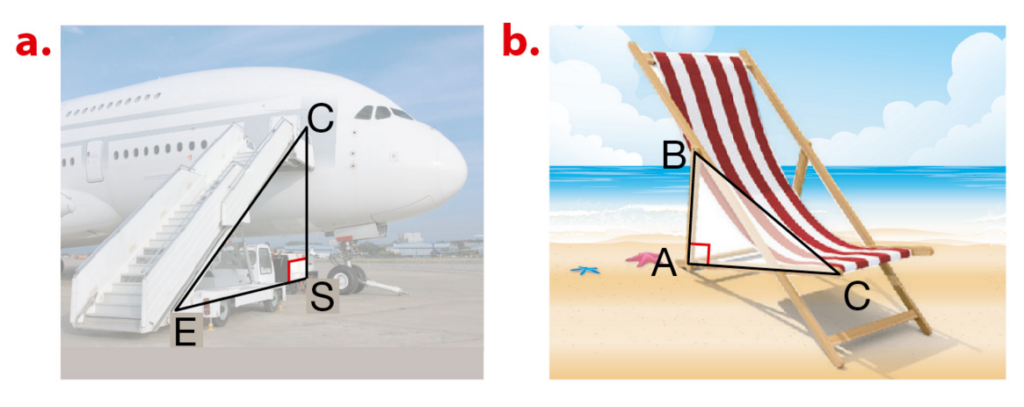
Exercice 62 :
Pour le triangle rectangle repéré sur chaque photo, appliquer le théorème de Pythagore.
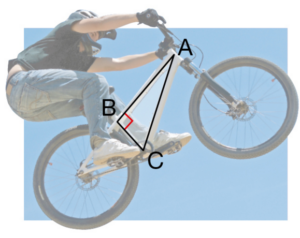
Exercice 63 :
Le cadre de ce BMX est un triangle ABC rectangle en B avec :
AB = 50 cm et BC = 20 cm.
Donner une valeur approchée au dixième près de cette longueur.
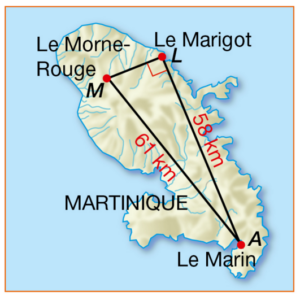
Exercice 64 :
Sur cette carte de Martinique, le triangle MLA (où M désigne Le Morne-Rouge, L Le Marigot et A Le Marin) est rectangle en L.
Utiliser les informations codées, pour calculer la distance LM à vol d’oiseau, en km.
Donner une valeur approchée au dixième près de cette distance.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «théorème de Pythagore : exercices de maths en 4ème corrigés en PDF.» au format PDF.
Ressources de quatrième
Cours de quatrième
Exercices de quatrième
D'autres cours et exercices à consulter
🤖 Exercices IA Interactifs ✨

Des milliers d'exercices interactifs conformes aux programmes officiels. Apprenez, pratiquez et progressez à votre rythme.
Exercices interactifsL'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.