Pyramides et cônes : cours de maths en 4ème en PDF.
Mis à jour le 27 avril 2025
I. Pyramide et cône de révolution en perspective :
0. Introduction :
Nous trouvons des pyramides ou des cônes dans la vie de tous les jours.
Par exemple les fameuses pyramides de Gizeh (Khéops, Khéphren et Mykérinos) ou la pyramide du Louvre (Paris).
Pour les cônes : les cônes de circulation routière en blanc et rouge ou encore dans les phénomène d’éruption volcanique, la lave bouillonne sous forme d’une élévation volcanique.
1. La pyramide :
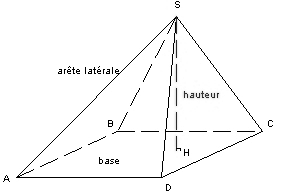
Une face est un polygone : c’est la base de la pyramide.Les autres faces, appelées faces latérales, sont des triangles qui ont un sommet commun.La hauteur d’une pyramide est le segments issu du sommet et perpendiculaire à la base.Les arêtes latérales sont les segments joignant les sommets de la base au sommet de la pyramide.
Remarque :
Une pyramide régulière est une pyramide dont la base est un polygone régulier ( par exemple un triangle équilatéral ou un carré) et dont les faces latérales sont des triangles isocèles superposables.
Exemple :
Tracer une pyramide en perspective et décrire les éléments de ce solide.
– Le sommet de cette pyramide est le point S.
– La base de cette pyramide est le quadrilatère ABCD.
– Les faces latérales sont : SAB, SBC, SCD, SDA.
– Les arêtes latérales sont : [AS], [BS], [CS], [DS].
– La hauteur de la pyramide est le segment [SH].
2. Le cône :
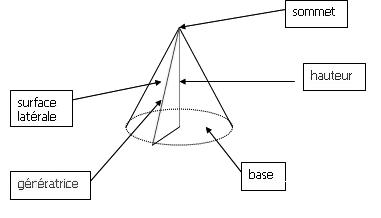
Un cône de révolution est un solide qui est généré par un triangle rectangle en rotation autour d’un des côtés de son angle droit.• La base du cône de révolution est un disque.La hauteur du cône de révolution est le segment qui joint le centre de ce disque au sommet du cône; il est perpendiculaire au disque de base.
Remarque :
La surface latérale d’un cône, appelée aussi développement, est générée par l’hypoténuse du triangle rectangle.
Elle a la forme d’un secteur de disque.
Exemple :
Tracer un cône en perspective et décrire les éléments de ce solide.
– Le sommet du cône est le point S.
– La base de ce cône est le disque de centre O: on la représente en perspective par un ovale ( une ellipse ) car elle n’est pas vue de face.
– La hauteur du cône est le segment [OS].Le triangle AOS, rectangle en O, génère le cône en tournant autour de l’axe (OS).
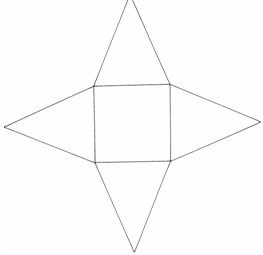
Patron d’une pyramide régulière à base carrée :
II. Calcul du volume d’une pyramide ou d’un cône :
Formule :
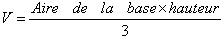
Remarque :
Le volume d’un cône de hauteur h et de rayon de base r est :
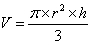
Exemples :
a. Calculer le volume d’une pyramide de hauteur 2,50 m ayant pour base un losange de diagonales 4 m et 4,20 m.
Réponse:
On calcul l’aire du losange de base :
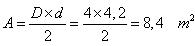
Puis, on calcule le volume :
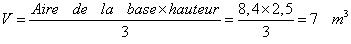
Conclusion:
Le volume de la pyramide vaut 7 mètres cube..
b. Calculer le volume dun cône de révolution de hauteur 25 cm ayant pour base un disque de rayon 9 cm.
Réponse :
On utilise la formule :
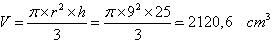
donc le volume du cône est à peu près 2 120,6 centimètres cube.
L’équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «pyramides et cônes : cours de maths en 4ème en PDF.» au format PDF.
Ressources de quatrième
Cours de quatrième
Exercices de quatrième
Nos applications
Téléchargez gratuitement la dernière version de nos applications.
