Cette épreuve fait intervenir les notions suivantes du collège :
- L’étude d’un centre de loisirs avec un bâtiment et d’un espace extérieur avec le théorème de Pythagore et le théorème de Thalès ainsi que, le calcul de l’aire d’une surface;
- Un QCM sur les probabilités, les pourcentages, la translation et l’homothétie;
- Un programme de calcul avec du calcul littéral;
- L’étude d’une fonction carrée et de sa courbe;
- Un programme avec Scratch pour réalisé des frises;
- Les ventes d’un marchand de glace et le volume d’une boule.
Ce sujet du brevet de maths 2023 en Asie Pacifique est à téléchargé en PDF avec son corrigé.
Ce document permet aux élèves de réviser leur DNB au collège et de se préparer dans les meilleures conditions.
BREVET DE MATHÉMATIQUES
Série générale
Durée de l’épreuve : 2 h 00 – 100 points
Exercice 1 (22 points)
Un centre de loisirs dispose d’un bâtiment et d’un espace extérieur pour accueillir des enfants.
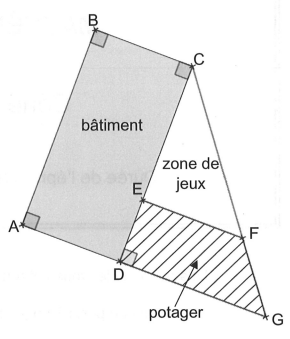
L’espace extérieur, modélisé par un triangle, est partagé en deux parties : un potager (quadrilatère DEFG hachuré) et une zone de jeux (triangle EFC), comme représenté par la figure ci-dessous.
Données :
- Les points C, E et D sont alignés.
- Les points C, F et G sont alignés.
- Les droites (EF) et (DG) sont parallèles.
- Les droites (DG) et (CD) sont perpendiculaires.
- CE = 30 m ; ED = 10 m et DG = 24 m.
1)Déterminer la longueur CD.
2) Calculer la longueur CG. Arrondir au dixième de mètre près.
3) L’équipe veut séparer la zone de jeux et le potager par une clôture représentée par le
segment [EF].
Montrer que la clôture doit mesurer 18 m.
4) Pour semer du gazon sur la zone de jeux, l’équipe décide d’acheter des sacs de 5 kg de
graines à 22,90 € l’unité. Chaque sac permet de couvrir une surface d’environ 140 m².
Quel budget doit-on prévoir pour pouvoir semer du gazon sur la totalité de la zone de jeux ?
5) La directrice du centre affirme que la surface du potager est plus grande que celle de la
zone de jeux. A-t-elle raison ?
Exercice 2 (18 points)
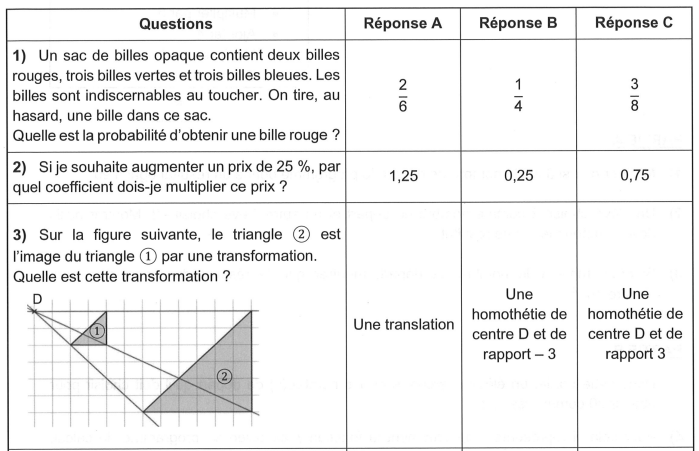
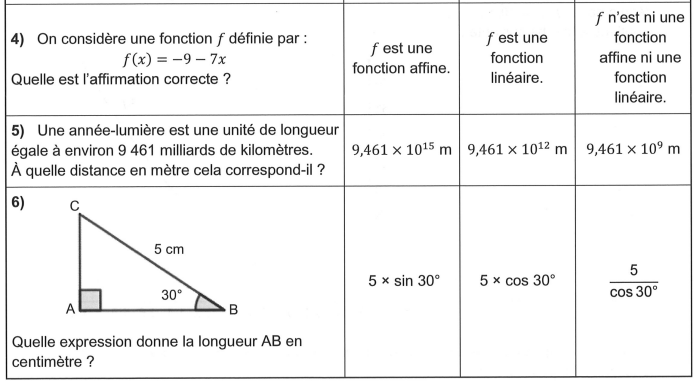
Cet exercice est un questionnaire Choix multiples (QCM). Aucune justification n’est
demandée.
Pour chaque question, trois réponses (A, B et C) sont proposées. Une seule réponse est
exacte. Recopier le numéro de Ia question et la réponse sur la copie.
Exercice 3 (20 points)
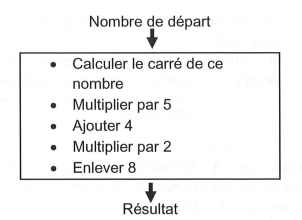
On considère le programme de calcul suivant :
PARTIE A
1) Montrer que si 3 est le nombre de départ, le programme donne un résultat égal à 90.
2) Un élève choisit 2 comme nombre de départ et un autre élève choisit —2. Montrer qu’ils
doivent obtenir le même résultat.
3) Si on nomme 
le nombre de départ, montrer que le résultat du programme peut s’écrire .
PARTIE B
Dans cette partie, un élève cherche le ou les nombre(s) de départ qu’il doit choisir pour
obtenir 30 comme résultat.
4) Pour cela, il représente graphiquement la fonction associée au programme de calcul,
définie par: .
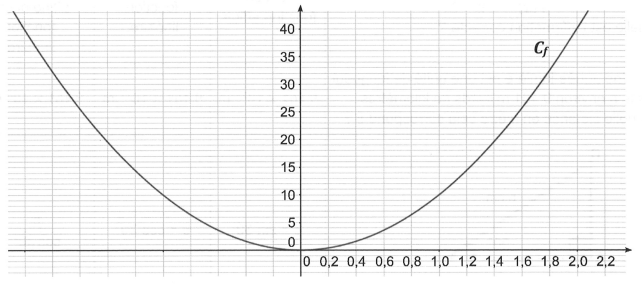
Il obtient la courbe suivante :
A l’aide du graphique, déterminer une valeur approchée des antécédents de 30 par la fonction f.
Ne pas justifier.
5) L’élève souhaite trouver une valeur plus précise de l’antécédent positif trouvé à la question
précédente.
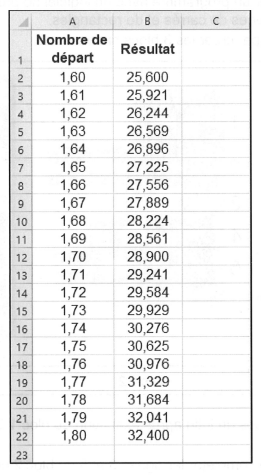
Pour cela, il utilise une feuille de calcul dont un extrait est donné ci-dessous :
a. Quelle formule a-t-il pu entrer dans la cellule B2 avant de l’étirer vers le bas ? Ne pas
justifier.
b. Dans ce tableau, quel est le nombre de départ donnant le résultat le plus proche de 30 ?
Ne pas justifier.
6) Déterminer la valeur exacte du nombre positif cherché par l’élève.
Exercice 4 (16 points)
Dans cet exercice, aucune justification n’est demandée.
Une élève souhaite réaliser un programme avec un logiciel de programmation pour dessiner des frises constituées de carrés et de rectangles.
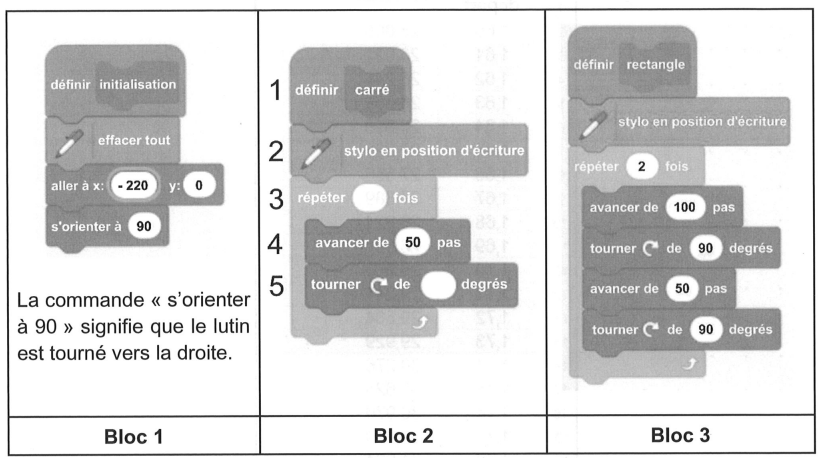
Pour cela, elle commence par créer les 3 blocs ci-dessous :
1) Quelles sont les coordonnées du lutin après exécution du bloc 1 ?
2) Par quelles valeurs doit-on compléter les lignes 3 et 5 du bloc 2 pour obtenir un carré ?
3) Construire ce que dessine le lutin lorsque le bloc 3 est utilisé. On prendra 1 cm pour 20 pas.
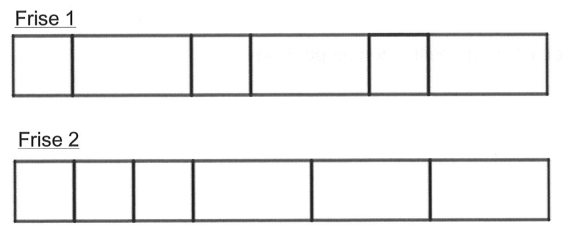
4) L’élève souhaite réaliser les deux frises ci-dessous.
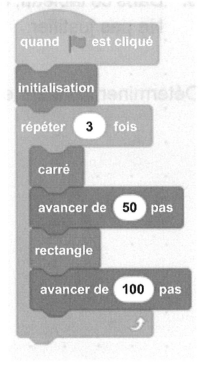
a. Elle rédige le script ci-dessus. Indiquer le numéro de la frise qu’elle va obtenir lorsque le drapeau vert est cliqué.
b. Écrire un script permettant de réaliser la frise qui n’a pas été obtenue.
Exercice 5 (24 points)
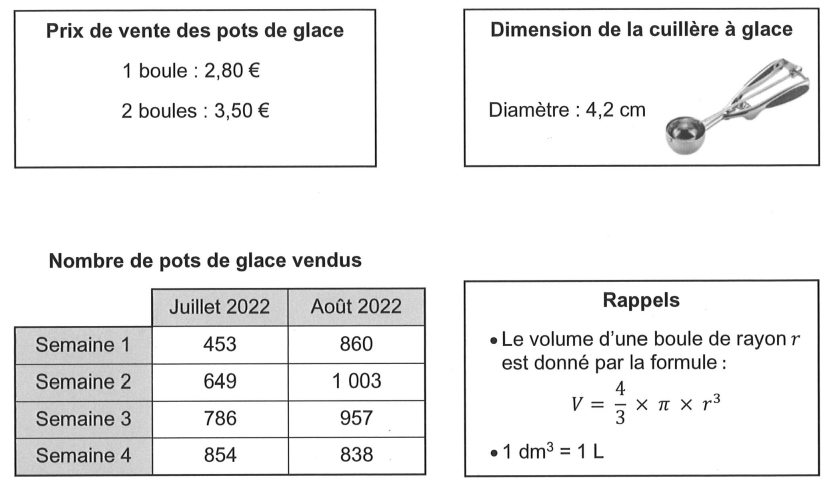
Un marchand de glaces souhaite préparer ses ventes pour l’été prochain.
Voici quelques informations concernant son activité en juillet et août 2022.
1) Calculer le nombre moyen de pots de glace vendus par semaine au cours de la période de
juillet août 2022.
2) Parmi tous les pots de glace vendus au cours de cette période, 67 % sont des pots à une
boule.
Calculer la somme que rapporte la vente des pots de glace au cours de cette période.
3) On modélise les boules de glace réalisées avec la cuillère glace par des boules de 4,2 cm de diamètre.
a. Montrer que le volume d’une boule de glace est d’environ 39 .
b. Le vendeur utilise des bacs de glace contenant 10 L chacun.
Combien peut-il faire de boules de glace, au maximum, avec la glace contenue dans un bac ?
Signaler une erreur
Aidez-nous à améliorer cette page en signalant une erreur
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «asie Pacifique : brevet de maths 2023 avec sujet et corrigé du DNB en PDF.» au format PDF.
Réviser les leçons et les exercices avec nos Q.C.M :
D'autres utilitaires pour progresser en autonomie :
