Géométrie dans l’espace : exercices de maths en 1ère corrigés en PDF.
Mis à jour le 29 juillet 2025
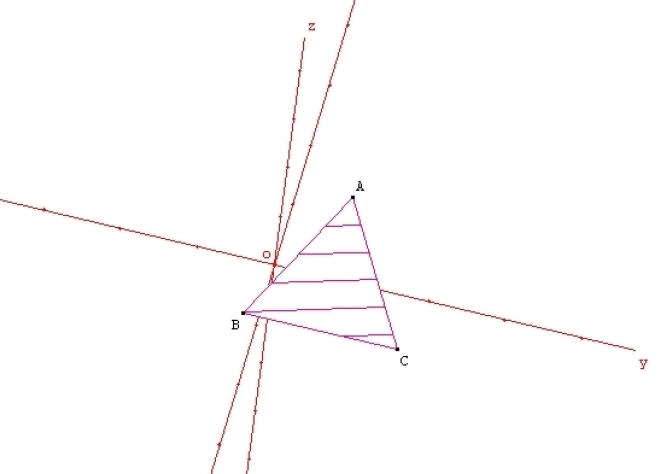
Exercice 1 – Cercle et lieux de points
Il est vivement recommandé d’utiliser un logiciel de géométrie…
1. Partie préliminaire :
on considère un triangle ABC, G son centre de gravité,
Ω le centre de son cercle circonscrit et H son orthocentre.
Montrer que H est l’image de Ω dans une homothétie de centre G dont on précisera le rapport.
2. On considère un cercle Γ de centre O, de rayon R, passant par un point fixe A.
Soient B et C deux points de Γ tels que la distance BC soit constante et égale à l.
a. Quel est le lieu géométrique des milieux I de [BC] ?
b. Quel est le lieu géométrique des centres de gravité G de ABC ?
c. Quel est le lieu géométrique des orthocentres H de ABC ?
3. Reprendre la partie 2. avec BC sur une droite ∆ ne passant pas par A, A fixe.
Exercice 2 – Homothéties et droites parallèles
ABC est un triangle isocèle (AB = AC).
E et F sont deux points du segment [BC].
Les parallèles à (AB) menées par E et F coupent (AC) en G et H respectivement.
Les parallèles à (AC) menées par E et F coupent (AB) en I et J respectivement.
1. Montrer que GH = IJ.
2. Quelle condition doivent vérifier E et F pour que (JG) et (IH) soient parallèles ?
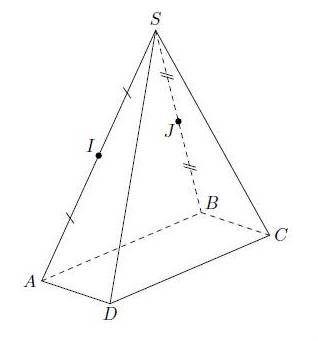
Exercice 3 – Pyramide à base triangulaire
La pyramide SABCD est à base rectangulaire.
On appelle I le milieu de [SA] et J le milieu de [SB].
Déterminer l’intersection des plans (DIJ) et (SAC).
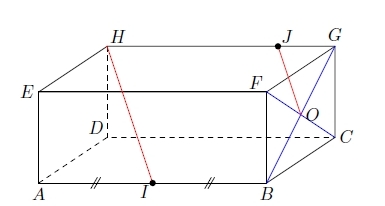
Exercice 4 – Etude d’un pavé droit
ABCDEFGH est un pavé droit.
On note I le milieu de l’arête [AB] et J le point tel que .
O est le centre de la face BCGF.
Démontrer que les droites (IH) et (JO) sont parallèles.
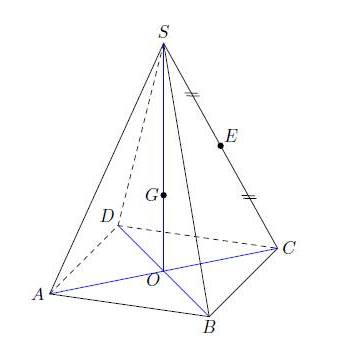
Exercice 5 – Etude d’une pyramide
SABCD est une pyramide à base carrée ABCD de centre O.
G est le centre de gravité du triangle SBD et E est le milieu du segment [SC].
Démontrer que les points A, G et E sont alignés.
Exercice 6 – Points coplanaires
L’espace est rapporté à un repère orthonormal direct .
On considère les points :
A(1 ; 0 ; – 1) B( – 1 ; 0 ; 0) C(1 ; – 6 ; 4) D(4 ; – 9 ; 5) E(3 ; – 6 ; 3)
1. Montrer que les points A, B, C et D sont coplanaires.
2. Montrer que le point D appartient à la droite (AE).
3. Montrer que ABCE est un parallélogramme. Est-ce un rectangle ? Est-ce un carré ?
Exercice 7 – Points alignés
On donne A (1 ; – 2 ; 3), B (0 ; 4 ; 4) et C (4 ; – 20 ; 9).
Les points A, B et C sont-ils alignés ?
Exercice 8 – Nature d’un triangle
On donne A(1 ; 1 ; 3),
Quelle est la nature du triangle ABC ?
Exercice 9 – Droites parallèles
On donne A( – 3 ; 1 ; 4), B( – 2 ; – 1 ; 7), C( – 4 ; – 1 ; – 2) et D(- 5 ;- 5 ; 4).
Les droites (AB) et (CD) sont-elles parallèles ?
Exercice 10 – Calculer les coordonnées d’un barycentre
On donne A(2 ; – 1 ; 3), B(1 ; 2 ; 0), C( – 2 ; 1 ; 2) et D( -1 ; – 2 ; 5).
1. ABCD est-il un parallélogramme ? Un rectangle ?
2. Calculer les coordonnées de l’isobarycentre du quadrilatère ABCD.
Exercice 11 :
Déterminer un vecteur normal à chacune des droites données par les équations cartésiennes
ci-dessous.
a) 2x+y – 3 = 0 b) – 3x + 5y = 0
c) 5x – 3y + 2 =0 d) – 2x – 4y + 1 =0
Exercice 12 :
déterminer un vecteur normal à chacune des droites définies par les deux points donnés.
a) B(- 3 ; 2) et C(1 ; – 2) b) F(1 ; 0) et G( – 3 ; 4)
c) M(0; – 2) et N(5 ; 4) d) H( – 2;3) et K( – 1; – 5)
Exercice 13 :
Dans chacun des cas, déterminer une équation cartésienne de la droite passant par le point donné
et de vecteur normal donné.
a) et
.
b) et
.
c) et
.
Exercice 14 :
On considère la droite d d’équation cartésienne 3x + y – 4 = 0 et le point B(2; – 3).
1)Donner un vecteur normal à la droite d.
2)En déduire une équation de la droite perpendiculaire à d passant par B.
3)En déduire les coordonnées du point K, projeté orthogonal du point B sur la droite d donnée.
Exercice 15 :
Pour chacune des équations suivantes, retrouver dans le tableau quel est son centre et son rayon.
Exercice 16 :
Dans chacun des cas suivants, déterminer le centre et le rayon du cercle si l’équation donnée
correspond bien à un cercle.
Exercice 17 :
On considère les équations suivantes :
et
.
1)Montrer que ces équations sont celles de deux cercles.
2)Pour chacun d’entre eux, donner son centre et son rayon.
3)Calculer la distance entre les deux centres.
4)Que peut-on en déduire sur la position des deux cercles ? Justifier.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «géométrie dans l’espace : exercices de maths en 1ère corrigés en PDF.» au format PDF.
Ressources de première
Cours de première
D'autres cours et exercices à consulter
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.



.JPG)











