Les fonctions : cours de maths en 1ère S à télécharger en PDF.

Sommaire de cette fiche

1 I. La fonction racine carrée :
- 1.1 1. Sens de variation de la fonction racine carrée :
- 1.2 2. Représentation graphique de la fonction racine carrée :
2 II. La fonction valeur absolue :
- 2.1 1. Valeur absolue d’un nombre réel :
- 2.2 2. La fonction valeur absolue :
  - 2.2.1 a. Sens de variation :
  - 2.2.2 b. Représentation graphique :
3 III. sens de variation des fonctions et :
- 3.1 1. Fonctions et :
- 3.2 2. Fonctions et :

Les généralités sur les fonctions numériques dans un cours de maths en 1ère S qui fait intervenir les tableaux de variation d’une fonction ainsi que sa représentation graphique.

Dans cette leçon en première S, nous étudierons le fonctions racine carrée et la valeur absolue ainsi que le sens de variation des fonctions u+k.

I. La fonction racine carrée :

Définition :

La fonction f définie sur $[0;+\infty[$ , qui à tout nombre réel positif x associe sa racine carrée $\sqrt{x}$ , est appelée fonction racine carrée.

1. Sens de variation de la fonction racine carrée :

Propriété :

La fonction $f:x \mapsto \sqrt{x}$ est croissante sur $[0;+\infty[$ .

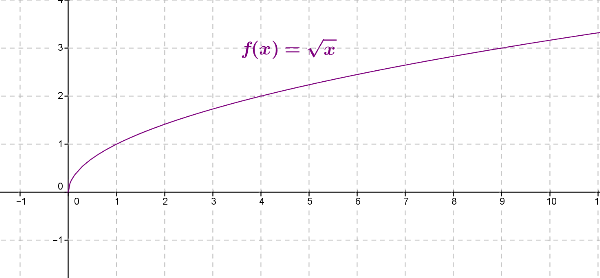
Courbe représentative de la fonction racine carrée :

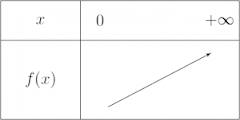
Tableau de variation :

Démonstration :

u et v désignent deux nombres réels positifs tels que $u\leq\, v$ .

Les deux nombres positifs $\sqrt{u}$ et $\sqrt{v}$ sont rangés dans le même ordre que leurs carrés.

$(\sqrt{u} )^2=u$ et $(\sqrt{v} )^2=v$ .

Or $0\leq\, u\leq\, v$ donc $\sqrt{0}\leq\, \sqrt{u}\leq\, \sqrt{v}$ , c’est à dire $f(u)\leq\, f(v)$ .

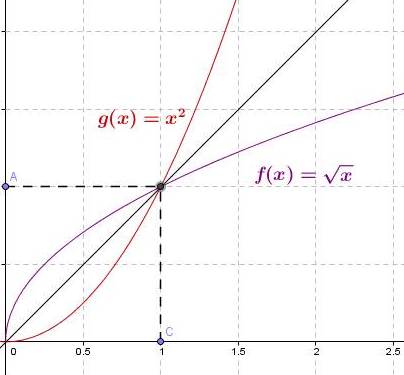
2. Représentation graphique de la fonction racine carrée :

Dans un repère orthogonal, $\zeta$ désigne la courbe représentative de la fonction racine carrée.

Propriété :

Dans un repère orthonormé, la courbe représentative $\zeta$ de la fonction racine carrée et la courbe représentative $\rho$ de la fonction carré sur $[0;+\infty[$ sont symétriques par rapport à la droite d’équation y=x.

Démonstration :

x et y désignent deux nombres réels positifs.

$y=\sqrt{x}$ équivaut à , c’est à dire :

appartient à $\zeta$ si, et seulement si, appartient à $\rho$ .

Propriété :

Pour tout nombre réel x de l’intervalle , $x^2\leq\, x\leq\, \sqrt{x}$ .

Pour tout nombre réel x de l’intervalle $[1;+\infty[$ , $\sqrt{x}\leq\, x\leq\, x^2$ .

II. La fonction valeur absolue :

1. Valeur absolue d’un nombre réel :

Définition :

Sur une droite graduée d’origine O, x est l’abscisse d’un point M.

La valeur absolue du nombre réel x, noté , est la distance OM.

Exemples :

$| 1-\sqrt{2} |=\sqrt{2}-1$

Propriété :

Pour tout nombre réel x,

$| x | \geq\, 0$ et .

2. La fonction valeur absolue :

Définition :

La fonction

définie sur $\mathbb{R}$ , qui à tout nombre réel x associe sa valeur absolue

, est appelée fonction valeur absolue.

a. Sens de variation :

Propriété :

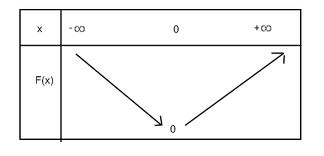
La fonction valeur absolue est décroissante sur $]-\infty;0]$ et croissante sur $[0;+\infty[$ .

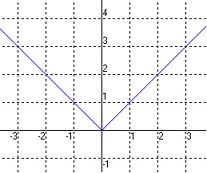
b. Représentation graphique :

Dans un repère orthogonal, la courbe représentative de la fonction valeur absolue est la réunion des demi-droites d’équations y=x sur $[0;+\infty[$ et y= – x sur $]-\infty;0]$ .

Propriété :

Dans un repère orthogonal, la courbe représentative $\zeta$ de la fonction valeur absolue est symétrique par rapport à l’axe des ordonnées.

Démonstration :

x et y désignent deux nombres réels.

M(x;y) appartient à la courbe $\zeta$ si, et seulement si, .

Or ceci équivaut à car , c’est à dire à M ‘ (- x; y) appartient à la courbe $\zeta$ .

III. sens de variation des fonctions $u+k,\lambda u,\sqrt{u}$ et $\frac{1}{u}$ :

1. Fonctions et $\lambda u$ :

Propriété :

u est une fonction définie sur un intervalle I et k un nombre réel.

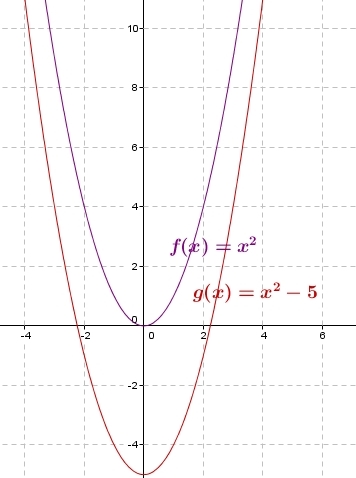
Les fonctions u et u+k ont le même sens de variation sur l’intervalle I.

Propriété :

u est une fonction définie sur un intervalle I et $\lambda$ un nombre réel non nul.

– Si $\lambda >0$ alors les fonctions et $\lambda u$ ont le même sens de variation sur I.

– Si $\lambda <0$ alors les fonctions et $\lambda u$ ont des sens de variation contraires sur I.

Exemples :

La fonction $x \mapsto x^2 -5$ a le même sens de variation sur $\mathbb{R}$ que la fonction carrée.

La fonction $x \mapsto -2\sqrt{x}$ est décroissante sur $[0;+\infty[$ .

2. Fonctions $\sqrt{u}$ et $\frac{1}{u}$ :

Propriété :

u est une fonction définie sur un intervalle I telle que, pour tout nombre réel x de I, $u(x)\geq\, 0$ .La fonction $x \mapsto \sqrt{u (x )}$ , notée $\sqrt{u }$ , a le même sens de variation que u sur l’intervalle I.

Propriété :

u est une fonction définie sur un intervalle I telle que, pour tout nombre réel x de I, $u(x)\neq 0$ et garde le même signe.La fonction $x \mapsto \frac{1}{u(x)}$ , notée $\frac{1}{u }$ , a un sens de variation contraire à celui de u sur I.

4.2/5 - (44 votes)

Télécharger et imprimer ce document en PDF gratuitement

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «généralités sur les fonctions numériques : cours de maths en 1ère S» au format PDF.

Télécharger nos applications gratuites avec tous les cours,exercices corrigés.

D'autres fiches similaires à généralités sur les fonctions numériques : cours de maths en 1ère S.

Mathovore vous permet de réviser en ligne et de progresser en mathématiques tout au long de l'année scolaire.
De nombreuses ressources destinées aux élèves désireux de combler leurs lacunes en maths et d'envisager une progression constante. Tous les cours en primaire, au collège, au lycée mais également, en maths supérieures et spéciales ainsi qu'en licence sont disponibles sur notre sites web de mathématiques.
Des documents similaires à généralités sur les fonctions numériques : cours de maths en 1ère S à télécharger ou à imprimer gratuitement en PDF avec tous les cours de maths du collège au lycée et post bac rédigés par des enseignants de l'éducation nationale.
Vérifiez si vous avez acquis le contenu des différentes leçons (définition, propriétés, téhorèmpe) en vous exerçant sur des milliers d'exercices de maths disponibles sur Mathovore et chacun de ces exercices dispose de son corrigé.
En complément des cours et exercices sur le thème généralités sur les fonctions numériques : cours de maths en 1ère S, les élèves de troisième pourront réviser le brevet de maths en ligne ainsi que pour les élèves de terminale pourront s'exercer sur les sujets corrigé du baccalauréat de maths en ligne.

Calcul littéral : correction des exercices en troisième
62
Développer avec les identités remarquables, exercices corrigés de mathématiques en troisième (3ème) sur les identités remarquables. Exercice: Développer en utilisant les identités remarquable : Exercice : On considère les expressions E = x² − 5x + 5 et F = (2x − 7)(x − 2) − (x − 3)² .…
Les équations et inéquations : correction des exercices en troisième
60
Résoudre des équations du premier degré à une inconnue.Exercices corrigés de mathématiques en troisième (3ème). Exercice : Exercice : Déterminer trois nombres entier positifs consécutifs dont la somme des carrés est égale à 1 325. Pour la facilité des calculs on choisira les nombres consécutifs suivants : n-1…
Problèmes de maths et calculs à résoudre à imprimer en PDF.
57
La série des problèmes ouverts de maths afin de réfléchir sur des exercices complexes avec un travail individuel ou en groupe.Ces exercices développe l'esprit d'initiative et le raisonnement scientifique pour les élèves du collège et du lycée. Une série de problèmes ouverts afin de développer la prise d'initiative et le…
Généralités sur les fonctions numériques : cours de maths en 2de
53
Les généralités sur les fonctions numériques dans un cours de maths en 2de où nous étudierons les opérations sur les fonctions ainsi que les égalités. dans cette leçon en seconde, nous aborderons le sens de variation d'une somme, produit et composée de fonctions numériques. I. Opérations algébriques sur les fonctions…
Les équations : exercices de maths en 3ème corrigés en PDF.
50
Des exercices de maths en troisième (3ème) sur les équations et équations produits. Résoudre des équations du premier degré en utilisant les différentes règles de calculs. Exercice 1 - Résoudre ces équations du premier degré Résoudre les équations suivantes : a) x + 0,6 = 4,8 b) -2 + x =…

Les dernières fiches mises à jour

Voici les dernières ressources mis à jour sur Mathovore (des cours, exercices, des contrôles et autres), rédigées par notre équipe d'enseignants.

Mathovore c'est 2 153 737 cours et exercices de maths téléchargés en PDF et 172 141 membres.
Rejoignez-nous : inscription gratuite.

I. La fonction racine carrée :

1. Sens de variation de la fonction racine carrée :

2. Représentation graphique de la fonction racine carrée :

II. La fonction valeur absolue :

1. Valeur absolue d’un nombre réel :

2. La fonction valeur absolue :

a. Sens de variation :

b. Représentation graphique :

III. sens de variation des fonctions <img class="LatexImg" src="https://mathovore.fr/cgi-bin/mimetex.cgi\?u+k,\lambda u,\sqrt{u}" alt="u+k,\lambda u,\sqrt{u}" /> et <img class="LatexImg" src="https://mathovore.fr/cgi-bin/mimetex.cgi\?\frac{1}{u}" alt="\frac{1}{u}" /> :

1. Fonctions <img class="LatexImg" src="https://mathovore.fr/cgi-bin/mimetex.cgi\?u+k" alt="u+k" /> et <img class="LatexImg" src="https://mathovore.fr/cgi-bin/mimetex.cgi\?\lambda u" alt="\lambda u" /> :

2. Fonctions <img class="LatexImg" src="https://mathovore.fr/cgi-bin/mimetex.cgi\?\sqrt{u}" alt="\sqrt{u}" /> et <img class="LatexImg" src="https://mathovore.fr/cgi-bin/mimetex.cgi\?\frac{1}{u}" alt="\frac{1}{u}" /> :

D'autres fiches similaires à généralités sur les fonctions numériques : cours de maths en 1ère S.

III. sens de variation des fonctions $u+k,\lambda u,\sqrt{u}$ et $\frac{1}{u}$ :

1. Fonctions et $\lambda u$ :

2. Fonctions $\sqrt{u}$ et $\frac{1}{u}$ :