Barycentre : exercices de maths en 1ère corrigés en PDF.

Le barycentre de nos points pondérés à travers des exercices de maths en 1ère corrigés avec l’utilisation de la définition du barycentre de n points pondérés et des propriétés du barycentre comme l’associativité. Tous ces énoncés en première disposent d’un corrigé détaillé afin que les élèves puissent réviser en ligne.

Exercice 1 – Barycentre de points pondérés
1. Construire le barycentre des points {(A,1);(B,2)} sachant que AB = 6 cm .
2. Construire le barycentre des points {(A,3);(B,-3)} sachant que AB = 8 cm .
3. Construire le barycentre des points {(A,1);(B,-2)} sachant que AB = 4 cm .
4. Construire le barycentre des points {(M,-3);(N,-2)} sachant que MN = 10 cm .

Exercice n° 2 :
1. Décrire l’ensemble des points M du plan tels que 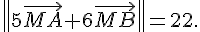$\|5\vec{MA}+6\vec{MB}\|=22 .$
2. Décrire l’ensemble des points M du plan tels que $\|-5\vec{MA}+8\vec{MB}\|=12 .$
3. Décrire l’ensemble des points M du plan tels que 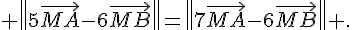$\|5\vec{MA}-6\vec{MB}\|=\|7\vec{MA}-6\vec{MB}\| .$
4. Décrire l’ensemble des points M du plan tels que 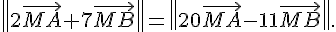$\|2\vec{MA}+7\vec{MB}\|=\|20\vec{MA}-11\vec{MB}\| .$

Exercice n° 3 :
Soit R un repère orthonormé du plan .
1. Construire le barycentre G des points {(A,2);(B,3)} sachant que les coordonnees, dans R, de ces points sont A(3;4) et B(-1;2) .
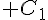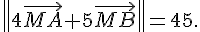2. On note l’ensemble des points M du plan tels que $\|4\vec{MA}+5\vec{MB}\|=45 .$ .
Déterminer l’équation de l’ensemble .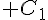
2. On note 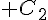l’ensemble des points M du plan tels que $\|3\vec{MA}+2\vec{MB}\|=\|7\vec{MA}-2\vec{MB}\| .$ .
Déterminer l’équation de l’ensemble .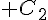

Trouver un lieu de points

ABC est un triangle équilatéral de côté 4 cm.
Déterminer l’ensemble 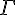$\Gamma$ des points M du plan tels que :
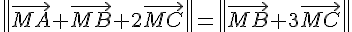$\|\vec{MA}+\vec{MB}+2\vec{MC}\|=\|\vec{MB}+3\vec{MC}\|$ .

Exercice 4 – Déterminer un lieu de points
Soit ABC un triangle isocèle en A tel que BC = 8 cm et BA = 5 cm.

Soit I le milieu de [BC].
1. Placer le point F tel que 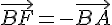$\vec{BF}=-\vec{BA}$ et montrer que F est le barycentre des points A et B pondérés par des réels que l’on déterminera.
2. P étant un point du plan, réduire chacune des sommes suivantes :
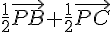
$\frac{1}{2}\vec{PB}+\frac{1}{2}\vec{PC}$
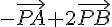
$-\vec{PA}+2\vec{PB}$
$2\vec{PB}-2\vec{PA}$
3. Déterminer et représenter l’ensemble des points M du plan vérifiant :
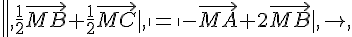
$\|,\frac{1}{2}\vec{MB}+\frac{1}{2}\vec{MC}|,,\|=\|-\vec{MA}+2\vec{MB}|,,\|$
4. Déterminer et représenter l’ensemble des points N du plan vérifiant :
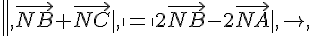
$\|,\vec{NB}+\vec{NC}|,,\|=\|2\vec{NB}-2\vec{NA}|,,\|$

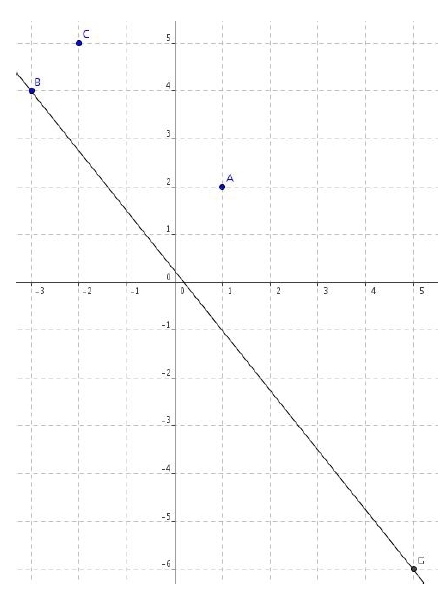
Exercice 5 – Exercice dans un repère
1. Placer dans un repère les points A(1,2); B(- 3 , 4) et C(- 2 , 5).
Soit G le barycentre des points pondérés (A,3), (B,2) et (C, – 4).
2. Quelles sont les coordonnées de G ?Placer G.
3. La droite (BG) passe-t-elle par l’origine du repère ? (Justifier)

Exercice 6 – Alignement de points
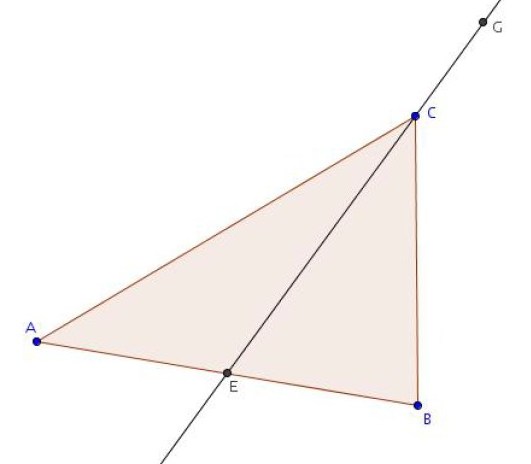
Dans le triangle ABC, E est le milieu de [AB] et G est le barycentre de (A,-2) (B,-2) (C,15).
Démontrer que G,C et E sont alignés .

Exercice 7 – Barycentre classique
ABCD est un quadrilatère et G est le barycentre de (A,1) (B,1) (C,3) (D,3).
Construire le point G. (Argumenter)

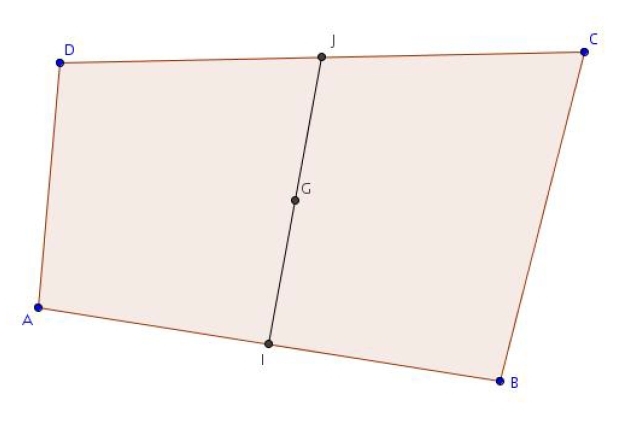
Exercice 8 – Isobarycentre et quadrilatère
ABCD est un quadrilatère.

On note G son isobarycentre.
Le but de cet exercice est de préciser la position de G.

1) On note I le milieu de [AB] et J le milieu de [CD].

Montrer que G est le barycentre de I et J munis de coefficients que l’on précisera.

2) Conclure et faire une figure.

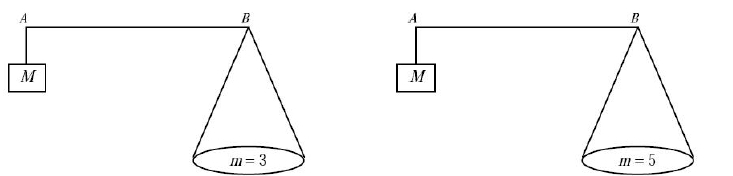
Exercice 9 – Sciences physiques

Une balance est constituée d’une masse M et d’un plateau fixé aux extrémités d’une tige.
Pour peser une masse m, le vendeur place à une position précise un crochet sur la tige.
Cette balance a l’avantage pour le commerçant de ne pas manipuler plusieurs masses.

1. Pour chacun des cas suivants, où faut-il fixer le crochet G sur le segment [AB] pour réaliser l’équilibre ?
(M = 2 kg)

On pourra reproduire ces schémas à l’échelle de son choix.

2. Le point G est tel que $\vec{AG}=\frac{2}{3}\vec{AB}$ .

Quelle est la masse m pesée ? (M = 2 kg).

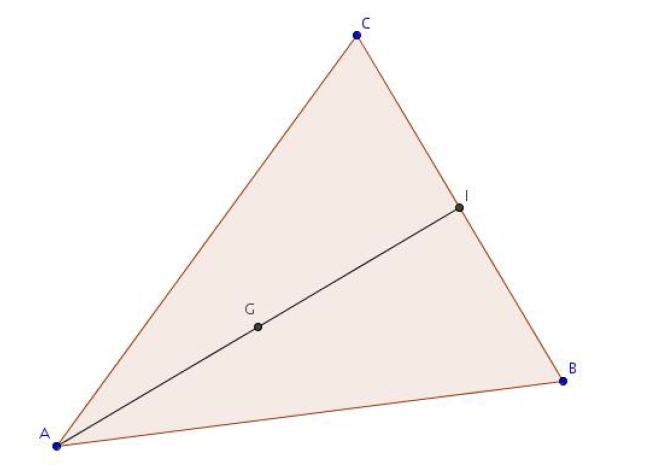
Exercice 10 – Déterminer la position d’un barycentre

ABC est un triangle. On note G le barycentre de (A ; 2), (B ; 1) et (C ; 1).

Le but de cet exercice est de déterminer la position précise du point G.

1. Soit I le milieu de [BC].

Montrer que :

$\vec{GB}+\vec{GC}=2\vec{GI}$

2. En déduire que G est le barycentre de A et I munis de coefficients que l’on précisera.

3. Conclure.

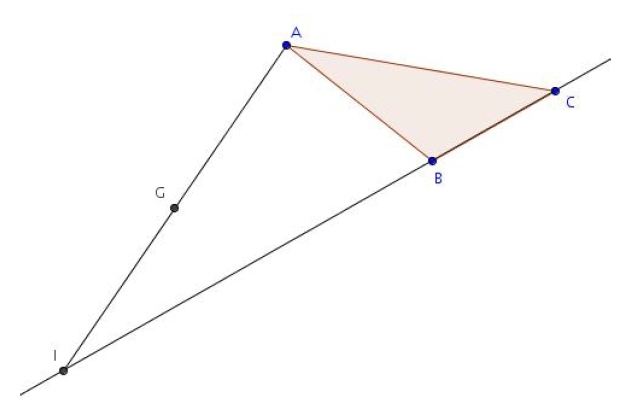
Exercice 11 – Construction et positionnement

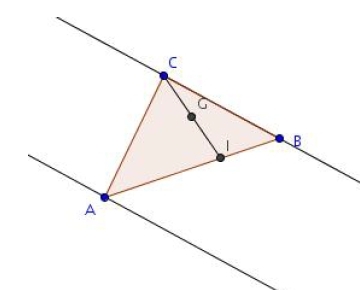
On considère un triangle ABC et l’on désigne par G le barycentre de (A ; 1), (B ; 4) et (C ; – 3).

1. Construire le barycentre I de (B ; 4) et (C ; – 3).

2. Montrer que 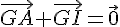$\vec{GA}+\vec{GI}=\vec{0}$ .

3. En déduire la position de G sur (AI).

Exercice 12 – Démontrer que des points sont alignés

Dans le triangle ABC, E est le milieu de [AB] et G est le barycentre de (A ; – 2), (B ; – 2) et (C ; 15).

Démontrer que G, C et E sont alignés.

Exercice 13 – Barycentres confondus

B est le milieu de [AC].
Démontrer que le barycentre de (A ; 1) et (C ; 3) est confondu avec celui de (B ; 2) et (C ; 2).

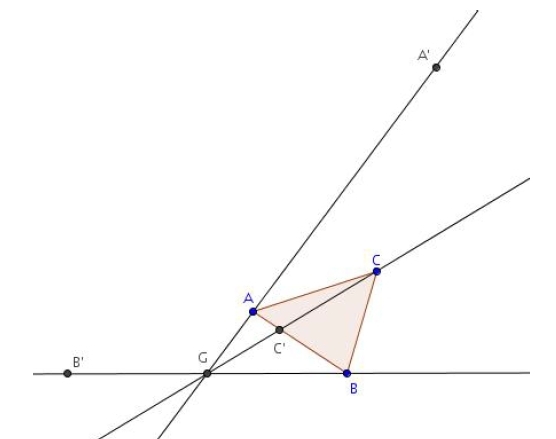
Exercice 14 – Construction de barycentre dans un triangle

ABC est un triangle.

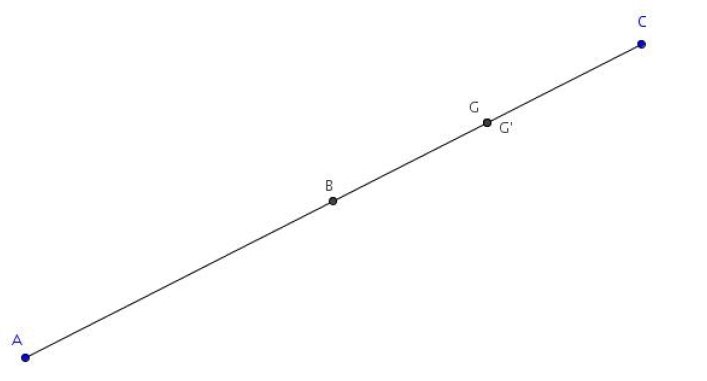
1. G est le barycentre de (A ; 1), (B ; 2) et (C ; 3). Construire le point G. Expliquer.

2. G ‘ est le barycentre de (A ; 1), (B ; 3) et (C ; – 3). Construire le point G ‘ . Expliquer.

3. Démontrer que (AG’) est parallèle à (BC).

Exercice 15 – Construction d’un barycentre

ABCD est un quadrilatère et G est le barycentre de (A ; 1), (B ; 1), (C ; 3) et (D ; 3).

Construire le point G. Expliquer.

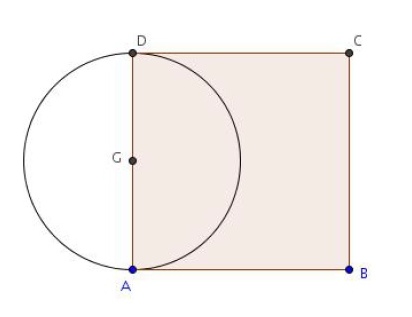
Exercice 16 – Ensemble de points
ABCD est un carré de centre G et de côté 4 cm.
1. Calculer la longueur GA .
2. Réduire la somme 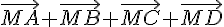$\vec{MA}+\vec{MB}+\vec{MC}+\vec{MD}$ ( à l’aide du point G).
3. Déterminer et représenter l’ensemble 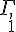$\Gamma,_1$ des points M tel que :
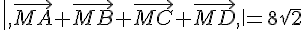
$,\|,\vec{MA}+\vec{MB}+\vec{MC}+\vec{MD},,\|=8\sqrt{2}$
4. Déterminer et représenter l’ensemble 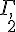$\Gamma,_2$ des points M tel que :
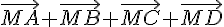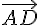$\vec{MA}+\vec{MB}+\vec{MC}+\vec{MD}$ soit colinéaire à $\vec{AD}$ .

Exercice 17 – Alignement de points
Dans le triangle ABC, le point E est le milieu de [AB]
et G est le barycentre de (A ; -2) (B;-2) et (C;8).
1. Exprimer E comme le barycentre de A et B .
2. Démontrer que G,C et E sont alignés .
3. C est-il le milieu de [EG] ?

Exercice 18 – Triangle équilatéral et droites parallèles

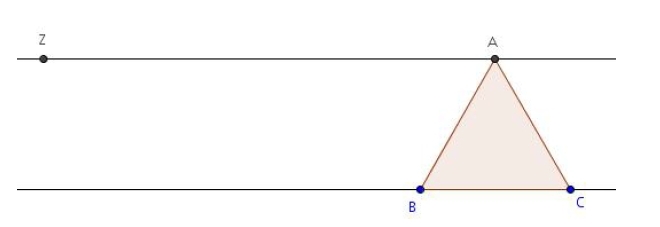
Soit ABC un triangle équilatéral de côté 3 cm.

1) Placer, en justifiant, le barycentre Z de (A ; 1), (B ; 3) et (C ; – 3).

2) Montrer que les droites (AZ) et (BC) sont parallèles.

Exercice 19 – Centre de gravité et droites concourantes
ABC est un triangle de centre de gravité G.
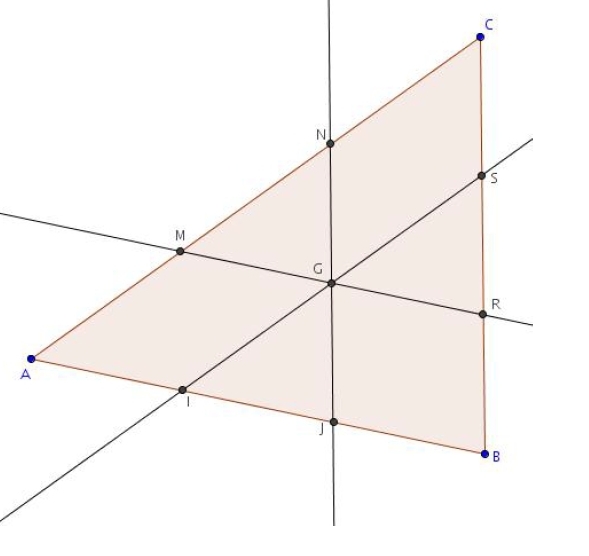
On note I, J, M, N, R et S les points définis par :
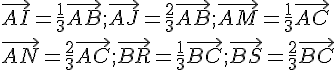
$\vec{AI}=\frac{1}{3}\vec{AB};\vec{AJ}=\frac{2}{3}\vec{AB};\vec{AM}=\frac{1}{3}\vec{AC}\\\vec{AN}=\frac{2}{3}\vec{AC};\vec{BR}=\frac{1}{3}\vec{BC};\vec{BS}=\frac{2}{3}\vec{BC}$
Démontrer que les droites (IS), (MR) et (NJ) sont concourantes en G.

Exercice 20 – Démontrer que des droites sont concourantes

ABC est un triangle.
On considère le barycentre A’ de (B ; 2) et (C ; – 3), le barycentre B ‘ de (A ; 5) et (C ; – 3)
et le barycentre C ‘ de (A ; 5) et (B ; 2).

Démontrer que les droites (AA ‘), (BB ‘) et (CC ‘) sont concourantes.

Voir Exercices 11 à 20...

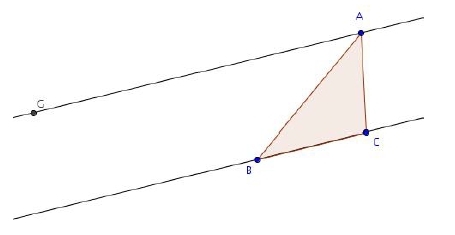
Exercice 21 – Démontrer que des droites sont parallèles

ABC est un triangle. Soit G le barycentre de (A ; 1), (B ; 3) et (C ; – 3).

Démontrer que les droites (AG) et (BC) sont parallèles.

Exercice 22 – Barycentre et repère

1. Placer dans un repère les points A(1 ; 2), B( – 3 ; 4) et C( – 2 ; 5).

Soit G le barycentre des points pondérés (A ; 3), (B ; 2) et (C ; – 4).

2. Quelles sont les coordonnées de G? Placer G.

3. La droite (BG) passe-t-elle par l’origine du repère ? Justifier.

Exercice 23 – Un lieu géométrique
[AB] est un segment de longueur 10 cm et G bar {(A ; 2) , (B ; 3)}
1. Développez et réduire 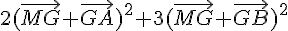$2(\vec{MG}+\vec{GA})^2+3(\vec{MG}+\vec{GB})^2$
2. Démontrez alors que pour tout point M du plan on a 2MA² + 3MB² = 5MG² + 120.
3. Déterminez alors et représentez l’ensemble des points M du plan tels que 2MA² + 3MB² = 245.

Exercice 24 – Ensemble de points
A, B et C sont 3 points du plan non alignés et k un nombre réel quelconque.
I bar { (B ;1), (C ;2)} et G le barycentre de (A, k), (B, 1- k) et (C, 2)
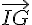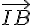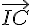1. Exprimer $\vec{IG}$ en fonction de $\vec{IA}$ , $\vec{IB}$ et $\vec{IC}$ .
2. Simplifier l’expression obtenue au 1. et en déduire l’ensemble (E) des points G lorsque k décrit $\mathbb{R}$ .
3. Représentez graphiquement (E) dans le cas AB = 5 cm, BC = 6 cm , AC = 5,5 cm.

Exercice 25 – Associativité du barycentre
A, B, C et D sont quatre points distincts.
On note K le barycentre de (A, 3) (B, 1), J le milieu de [DC], G le centre de gravité de BCD et I le milieu de [AG].
Montrer que les points I, J et K sont alignés.

Exercice 26 – Barycentre et paramètre
ABC un triangle ; à tout réel m, on associe le point G_m barycentre de (A ; 2) ; (B ; m) et (C ; – m).
On note O le milieu de [BC].
1.      Expliquer pourquoi G_m existe toujours et démontrer que, lorsque m décrit $\mathbb{R}$ , G_m décrit une droite D que vous préciserez.
2.      a) Construisez G₂ et G_-2 . Avec AB= 4cm , AC = 3cm et BC = 6cm
b) On suppose m différent de 2 et -2.
Soit G_m un point de D distinct de A, G₂ etG_-2 .
Démontrer que (BG_m) coupe (AC) en un point noté I et que (CG_m) coupe (AB) en un point noté J.
3.      Dans le repère 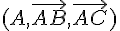$(A,\vec{AB},\vec{AC})$ ,
calculez en fonction de m les coordonnées de I et J.
Déduisez-en que les points O, I et J sont alignés.
(On pourra utiliser la condition analytique de colinéarité de 2 vecteurs).

Exercice 27 – Centre de gravité
Soit ABC un triangle, A’ , B’ , et C’ les milieux des côtés opposés à A, B et C respectivement, M un point donné.
On note A₁, B₁et C₁les symétriques du point M par rapport à A’ , B’ , et C’ .
On désigne par M’ barycentre des points  (A, 1) (B,1) (C,1) et (M,-1)
1.      Montrer que les droites (AA₁) ; (BB₁) et (CC₁) sont concourantes en M ‘.
2.      Soit G le centre de gravité de ABC. Montrer que M ‘ , M et G sont alignés et préciser la position de M ‘ sur la droite (MG).

Exercice 28 – Trouver un ensemble de points du plan
ABCD est un carré.

1. Quel est l’ensemble E des points M du plan tels que :

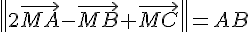
$\| 2\vec{MA}-\vec{MB}+\vec{MC} \|=AB$

2. Représenter cet ensemble E.

Exercice 29 – Carré

Soit ABCD un carré et K le barycentre des points pondérés (A ; 2), (B ; – 1), (C ; 2) et (D ; 1).

On note I le barycentre des points pondérés (A ; 2) et (B ; – 1), et J celui de (C ; 2) et (D ; 1).

1. Placer I et J en justifiant.

2. Réduire l’écriture des vecteurs suivants :

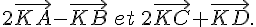
$2\vec{KA}-\vec{KB}\,et\,2\vec{KC}+\vec{KD}.$

En déduire que K est le barycentre de (I ; 1) et (J ; 3).

3. Placer K en justifiant.

Exercice 30 – Barycentre et placement de points

Soit ABC un triangle et G un point vérifiant :

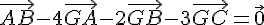
$\vec{AB}-4\vec{GA}-2\vec{GB}-3\vec{GC}=\vec{0}$

Le point G est-il le barycentre des points pondérés (A ; 5), (B ; 1) et (C ; 3) ? Justifier.

Voir Exercices 21 à 30...

Exercice 31 – Isobarycentre, centre de gravité et repère
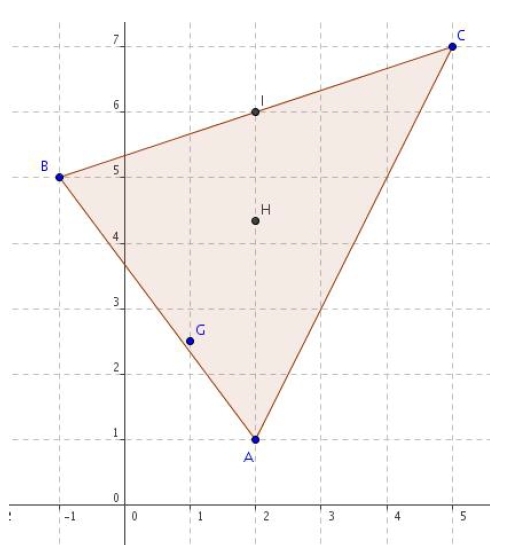
Dans un repère 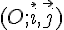$(O;\vec{i},\vec{j})$ ,

1.Placer les points A(2 ; 1), B( – 1 ; 5), C(5 ; 7) et G(1 ; 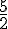$\frac{5}{2}$ ).

2. Déterminer les coordonnés de l’isobarycentre I des points B et C.

3. Déterminer les coordonnées du centre de gravité H du triangle ABC.

4. Existe-t-il un réel k tel que G soit barycentre de (A ; 1) et (B ; k) ? Justifier.

Exercice 32 – Ensemble de points
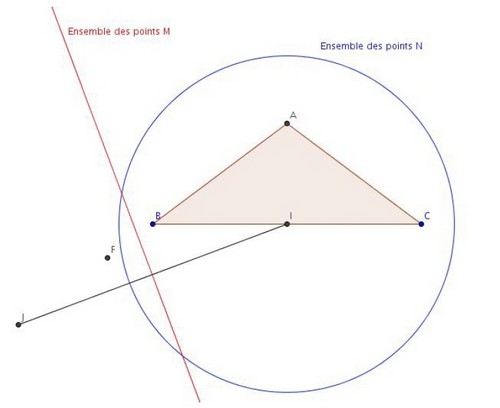
Soit ABC un triangle isocèle en A tel que BC = 8 cm et BA = 5 cm. Soit I le milieu de [BC].
1. Placer le point F tel que 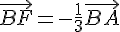$\vec{BF}=-\frac{1}{3}\vec{BA}$ .
et montrer que F est le barycentre des points A et B pondérés par des réels que l’on déterminera.

2. P étant un point du plan, réduire chacune des sommes suivantes :

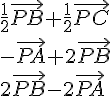
$\frac{1}{2}\vec{PB}+\frac{1}{2}\vec{PC}\\-\vec{PA}+2\vec{PB}\\2\vec{PB}-2\vec{PA}$

3. Déterminer et représenter l’ensemble des points M du plan vérifiant :

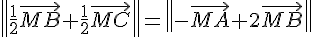
$\|\frac{1}{2}\vec{MB}+\frac{1}{2}\vec{MC} \|= \| -\vec{MA}+2\vec{MB} \|$

4. Déterminer et représenter l’ensemble des points M du plan vérifiant :

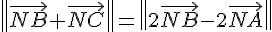
$\|\vec{NB}+\vec{NC} \|= \| 2\vec{NB}-2\vec{NA} \|$

Voir Exercices 31 à 32...

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «barycentre : exercices de maths en 1ère corrigés en PDF.» au format PDF.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

Réviser les leçons et les exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres utilitaires pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathovore c'est 14 099 023 cours et exercices de maths téléchargés en PDF.