Le parallélogramme : corrigé des exercices de maths en 5ème en PDF.

Mis à jour le 28 mai 2025

Sommaire

🔍Corrigés Détaillés

5eme • Scolaire

Le parallélogramme

🔎 Analyse : 15 min

🎯 Niveau : Scolaire

📱 Format : Gratuit

📄 PDF : Disponible

Le corrigé des exercices de maths en 5ème sur le parallélogramme. Savoir construire un parallélogramme à l’aide du matériel de géométrie (règle, compas, équerre et rapporteur). Utiliser les propriétés pour effectuer des démonstrations.

Exercice 1 :

Exercice 2 :

1. Construire un parallélogramme DOMI tel que :

DM= 7cm , $\widehat{MDO}=32^{\circ}$ et $\widehat{DMO}=58^{\circ}$ .

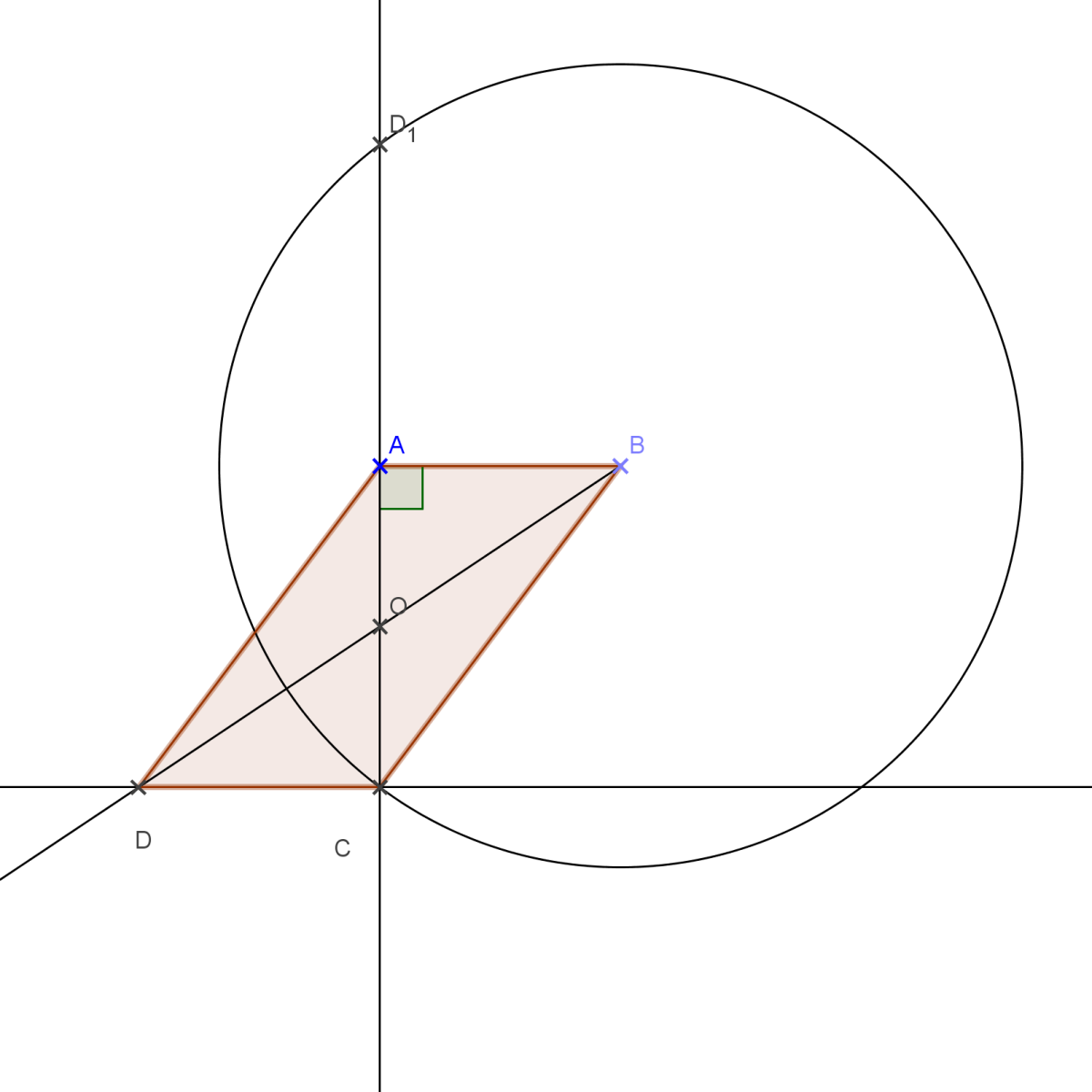
2. Démontrer que le quadrilatère DOMI est un rectangle .

Calculons la mesure d’angle $\widehat{DOM}$ .

$\widehat{DOM}=180-32-58=180-90=90$ °.

DOMI est un parallélogramme ayant un angle droit, c’est donc un rectangle .

Exercice 3 :

Exercice 4 :

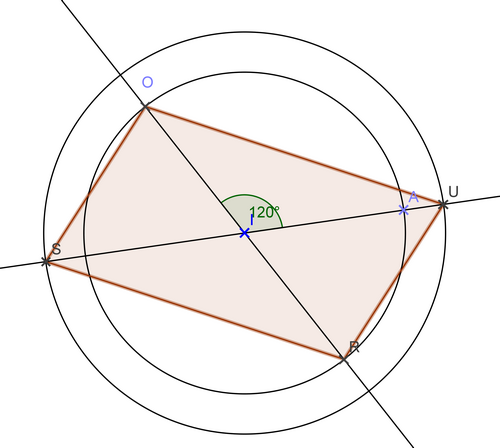
Voici la construction du parallélogramme OURS :

Exercice 5 :

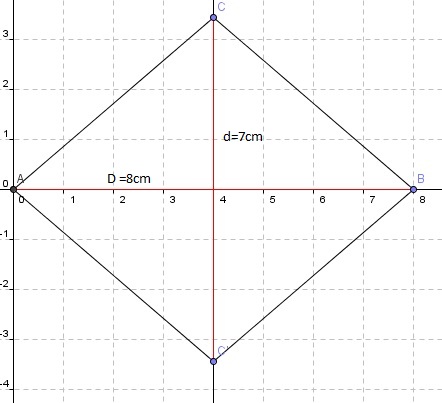
2. On a :

Aire de la surface du losange = $\frac{d+D}{2}$ =56/2=28cm²

Exercice 6 :

$\widehat{GEF}=180-(\widehat{EFG}+\widehat{EGF})$

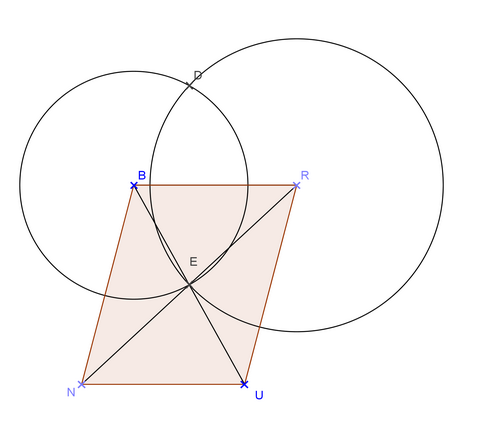
Et c’est à l’aide de cela qu’on prend le rapporteur. Qu’on le pointe en E et qu’on réalise un angle de 90°.

On s’aperçoit qu’il s’agit d’un quadrilatère bien particulier, appelé LOSANGE. qui a des diagonale [IG] et [FH]qui se coupent en leur milieu E (d’après la symétrie par rapport à E) et que ces diagonale sont perpendiculaires.

Exercice 7 :

Pour construire un parallélogramme il faut et il suffit de construire des parallèles.

Il s’agit d’un losange. E est le symétrique de I par rapport à l’axe (AB) donc il y a un angle droit entre [EI] et entre [AB]. Par symétrie, les diagonales de cette figure se coupent en leur milieu et sont perpendiculaires.

Exercice 8 :

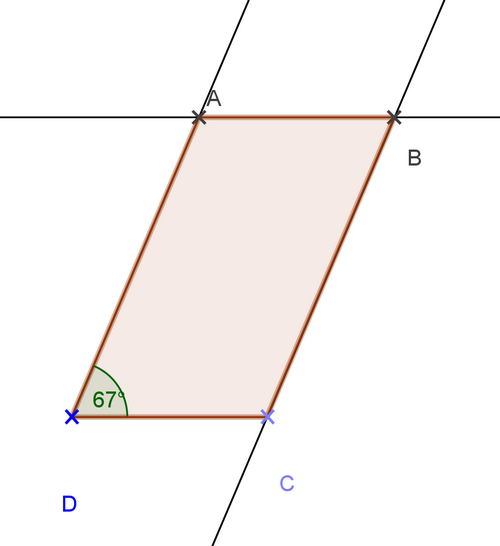
En regardant les mesurent des angles 180°-(110°+35°)=35° donc l’angle $\widehat{ABC}$ =35°

A partir de là à vous de construire la figure.

1°)Le triangle est isocèle.

2°) Encore un losange ;^) formé de deux triangle isocèles. (AD) perpendiculaire à (CB). Et les diagonales se coupent en leur milieu.

Exercice 9 :

Exercice 21 :

1. Les noms corrects sont PRCA et ARCP.

2. Les diagonales sont [AC] et [PR].

3. Le côté opposé à [PA] est [RC].

4. Les côtés consécutifs à [PC] sont [CA] et [AR].

5. L’angle opposé à $\widehat{PCR}$ est $\widehat{RCA}$ .

6. Les angles consécutifs à $\widehat{PAR}$ sont $\widehat{ARC}$ et $\widehat{RCP}$ .

Exercice 22:

1. Compléter les étiquettes grises sachant que bleu est un parallélogramme : ABLE.

2. La mesure de l’angle $\widehat{BLE}$ est 90 degrés car dans un parallélogramme, les angles opposés sont égaux.

3. La longueur de [BU] est égale à la longueur de [AL] car dans un parallélogramme, les côtés opposés sont de même longueur.

Exercice 23 :

La longueur de [TW] est égale à la longueur de [UW] car dans un parallélogramme, les côtés opposés sont de même longueur.

Exercice 24 :
(à compléter avec les figures et les constructions)

Exercice 25 :

1. La longueur du segment [TP] est égale à la longueur du segment [SR] car dans un parallélogramme, les côtés opposés sont de même longueur.

2. On peut déterminer la longueur de [SQ] car dans un parallélogramme, les côtés opposés sont de même longueur, donc [SQ] est égal à [PR].

3. En utilisant les propriétés des parallélogrammes et les mesures déjà données, on peut déterminer la longueur de [SP] en retrouvant les longueurs des autres côtés du parallélogramme.

Exercice 26 :

a. Le triangle OMC semble être isocèle.

b. En considérant les égalités de longueurs dans un parallélogramme, on peut montrer que les triangles OMC et OAC sont isométriques, donc le triangle OMC est bien isocèle.

Exercice 27 :

Les parallélogrammes possibles sont : AOIB, APOB, EOIA, EPIC, FDHA, FCGB.

Exercice 28 :

a. JK = 3 cm (car les côtés opposés d’un parallélogramme sont de même longueur).
b. LK = 4,2 cm (car les côtés opposés d’un parallélogramme sont de même longueur).
c. MI = 1,5 cm (car les côtés opposés d’un parallélogramme sont de même longueur).
d. LJ = 3 cm (car les côtés opposés d’un parallélogramme sont de même longueur).

Exercice 29 :

a. Le périmètre de LOIN est égal à la somme de tous ses côtés : LO + ON + NI + IL.
b. La mesure de l’angle \widehat{LNI} est égale à celle de l’angle \widehat{LOI} car les angles opposés d’un parallélogramme sont égaux.

Exercice 30 :

a. Le quadrilatère obtenu par symétrie par rapport à la droite verte est un rectangle.
b. Les dimensions du rectangle peuvent être déterminées en mesurant les côtés sur la figure.

Exercice 31 :

a. Le quadrilatère obtenu par symétrie par rapport à la droite rouge est un losange.
b. Les mesures des angles peuvent être déterminées en mesurant les angles sur la figure.

4.6/5 - (27158 votes)

×12

L’équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs

200+ Années cumulées

Quotidien Mise à jour

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «le parallélogramme : corrigé des exercices de maths en 5ème en PDF.» au format PDF.