Le parallélogramme : cours de maths en 5ème en PDF.
Mis à jour le 29 juin 2025
I. Définition et vocabulaire :
1. Rappels :
Un quadrilatère est une figure géométrique à 4 côtés.
Remarque :
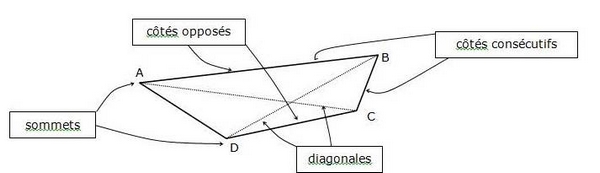
Attention à l’ordre des lettres. Les quadrilatères ABCD et ABDC sont différents.
2. Le parallélogramme :
Un parallélogramme est un quadrilatère qui a ses côtés opposés deux à deux parallèles.
ABCD est un parallélogramme : (AB)//(DC) et (AD)//(BC)
II. Propriétés : lien avec la symétrie centrale .
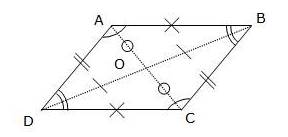
Dans un parallélogramme, le point d’intersection O des diagonales est le centre de symétrie du parallélogramme.
Remarque :
On dit alors que ABCD est un parallélogramme de centre O.
III. Conséquences
1. Les diagonales :
Les diagonales d’un parallélogramme se coupent en leur milieu.
Démonstration :
O est le centre de symétrie donc par définition 0 est le milieu de [AC] et de [BD].
2. Les côtés :
Les côtés opposés d’un parallélogramme sont de même longueur.
Démonstration :
Par symétrie par rapport à O, [AB] est l’image de [CD] et [AD] est l’image de [BC].
La symétrie centrale conserve les longueurs donc AB = CD et BC = AD.
3. Les angles :
Les angles opposés d’un parallélogramme sont égaux deux à deux.
Démonstration :
La symétrie centrale conserve les angles et comme un parallélogramme a pour centre de symétrie le point d’intersection de ses diagonales alors les angles opposés d’un parallélogramme sont de même mesure.
IV. Les parallélogrammes particuliers :
1.Le rectangle
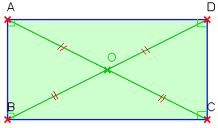
- Si un parallélogramme a un angle droit alors c’est un rectangle.
- Si un parallélogramme a ses diagonales de même longueur alors c’est un rectangle.
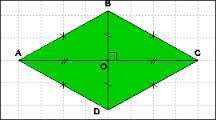
2.Le losange
- Si un parallélogramme a ses diagonales perpendiculaires alors c’est un losange.
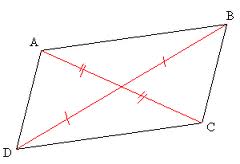
- Si un parallélogramme possède deux côtés consécutifs égaux alors c’est un losange.
Remarque :
Le losange possède deux axes de symétrie : ses diagonales.
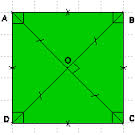
3.Le carré
Si un parallélogramme est à la fois un rectangle et un losange alors c’est un carré.
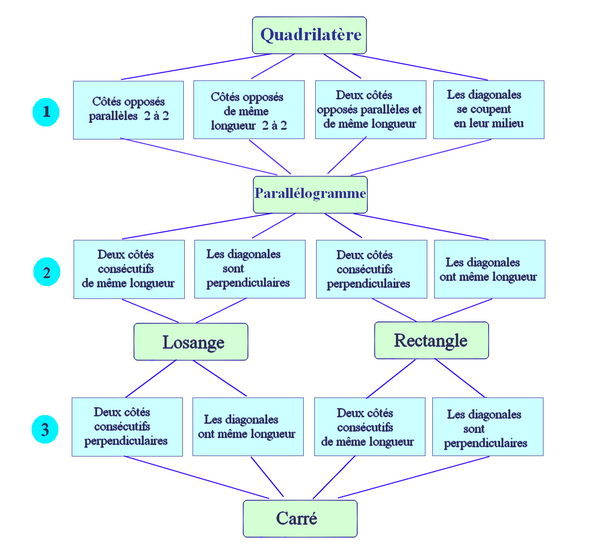
V.Bilan sur le parallélogramme :
L’équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «le parallélogramme : cours de maths en 5ème en PDF.» au format PDF.
Ressources de cinquième
Cours de cinquième
Exercices de cinquième
Nos applications
Téléchargez gratuitement la dernière version de nos applications.
