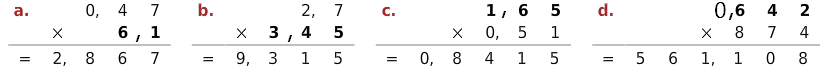Problèmes sur les 4 opérations : corrigé des exercices de maths en 6ème en PDF.
Mis à jour le 21 septembre 2025
Exercice 1 : problème d’argent
a. Alice trouve 5 € et l’ajoute aux 25 € qu’elle possède déjà. Elle a donc désormais :
25 € + 5 € = 30 €
b. Alice a 25 € dans son sac à main et dépense 5 € pour un gâteau. Pour savoir combien il lui reste, on soustrait 5 € à 25 € :
25 € – 5 € = 20 €
Il lui reste donc 20 € après avoir acheté le gâteau.
c. La maman d’Alice lui donne 25 € par mois comme allocation. Si elle ne le dépense pas, elle aura :
25 € (par mois) × 5 mois = 125 €
d. Alice et ses 5 sœurs mettent chacune 5 € dans leur tirelire chaque semaine pendant 25 semaines. Cela fait un total de :
5 € (par semaine) × 25 semaines = 125 € par personne
Puisqu’il y a 6 sœurs (dont Alice), elles auront un total de :
125 € × 6 = 750 €
A l’issue de cette période, leur maman leur versera à chacun 25 € supplémentaires, ils auront donc :
125 € (par personne) + 25 € (de maman) = 150 € par personne
Puisqu’ils regrouperont leurs économies, ils auront un total de :
150 € × 6 = 900 €
Maintenant, additionnons toutes les économies des sœurs : 750 € + 900 € = 1650 €.
Exercice 2 : problème du boxeur
a.Le boxeur pèse 97,3 kg et perdra 3 kg par mois. Pour savoir combien il va perdre, il faut calculer le nombre de mois avant le combat (puisqu’il est déjà à 4 mois du combat). Ainsi, on soustrait 4 mois au temps total jusqu’au combat :
Temps total jusqu’au combat – Temps déjà écoulé = Temps restant jusqu’au combat
? – 4 mois = ?
On sait qu’il va perdre 3 kg par mois, on multiplie donc le nombre de mois restant par 3 kg :
Temps restant jusqu’au combat × 3 kg/mois = ?
Maintenant, nous pouvons déterminer le nombre de mois restant avant le combat :
Temps restant avant le combat = ? mois
? mois × 3 kg/mois = Perte de poids
? mois × 3 kg/mois = 12 kg
Ainsi, le boxeur perdra au total 12 kg au cours de son régime.
b. Pour connaître son poids le jour du combat, on soustrait sa perte de poids de son poids initial :
Poids initial – Perte de poids = Poids final
97,3 kg – 12 kg = ?
97,3 kg – 12 kg = 85,3 kg
Ainsi, le jour du combat, le boxeur pèsera 85,3 kg.
Exercice 3 : problème d’une équipe de football
a. Le prix d’un équipement complet est la somme des prix des composants individuels :
Maillot (27 €) + Short (15 €) + Paire de chaussettes (6 €) = 27 € + 15 € + 6 € = 48 €
Ainsi, le prix d’un équipement complet est de 48 €.
b. Puisqu’il y a 16 joueurs dans l’équipe, le montant total nécessaire pour acheter de l’équipement pour toute l’équipe est de :
16 joueurs × 48 € (par équipement) = 768 €
c. Le sponsor reverse au club 150 €, qui sont déduits du montant total nécessaire à l’achat du matériel. Le magasin de sport propose également une réduction de 60 €.
Montant total nécessaire à l’achat du matériel – Cadeau du parrain – Remise = Montant à payer
768 € – 150 € – 60 € = ?
Calculons le résultat :
768 € – 150 € = 618 €
618 € – 60 € = 558 €
Ainsi, l’entraîneur doit débourser 558 € pour acheter du matériel pour toute l’équipe.
Exercice 4 : budget d’un club de foot
**Budget initial :** 100 M€
**Revenus de vente de joueurs :** 2 joueurs × 10 M€ par joueur = 20 M€
**Revenus :** 100 M€ (budget initial) + 20 M€ (revenus de vente de joueurs) = 120 M€
**Dépenses en nouveaux joueurs :** 4 joueurs × 15 M€ par joueur = 60 M€
**Dépenses totales :** 120 M€ (recettes) – 60 M€ (dépenses) = 60 M€
Il reste donc au club 60 M€ dans sa caisse.
Exercice 5 : problème du jeu vidéo
a. Lorsque Benoît aura complété les deux jeux, il aura :
87 monstres (version BLEUE) + 79 monstres (version ROUGE) = 166 monstres
Il aura donc 166 Pekomen.
b. Benoît a déjà trouvé :
33 monstres (version BLEUE) + 65 monstres (version ROUGE) = 98 monstres
Il y a un total de 166 Pekomen, et il en a déjà trouvé 98. Pour trouver les Pekomen restants, on soustrait :
166 Pekomen – 98 Pekomen = 68 Pekomen
Benoît a donc encore 68 Pekomen à retrouver.
c. Benoît a besoin d’environ 30 minutes pour retrouver chaque Pekomen. Pour retrouver les 68 Pekomen restants, il lui faut :
68 Pekomen × 30 minutes par Pekomen = 2040 minutes
Puisqu’il y a 60 minutes dans une heure, nous pouvons convertir cela en heures :
2040 minutes ÷ 60 = 34 heures
Benoît doit donc jouer environ 34 heures pour terminer les deux parties.
Exercice 6 : le cinéma
a. Chaque enfant paie :
* 6 € pour la place de cinéma
* 1,5 € pour le soda
* 2 € pour la glace
Coût total par enfant : 6 € + 1,5 € + 2 € = 9,5 €
Ainsi, chaque enfant paie 9,5 €.
b. Le coût total pour le groupe est :
* 3 filles × 9,5 € = 28,5 €
* 5 garçons × 9,5 € = 47,5 €
* Coût total : 28,5 € + 47,5 € = 76 €
Le groupe a donc dépensé au total 76 €.
c. Dans les autres cinémas, la place de cinéma coûte :
* 5,50 € par enfant
Le soda et la glace coûtent toujours :
* Soda : 1,5 € + 0,25 € = 1,75 €
* Glace : 2 € + 0,25 € = 2,25 €
Coût total par enfant : 5,50 € + 1,75 € + 2,25 € = 9,50 €
Ainsi, chaque enfant paierait 9,50 € dans ce cinéma.
d. Le coût total pour le groupe dans ce cinéma est de :
* 3 filles × 9,50 € = 28,5 €
* 5 garçons × 9,50 € = 47,50 €
* Coût total : 28,5 € + 47,50 € = 76,00 €
Le groupe dépenserait donc au total 76,00 € dans ce cinéma.
A noter que le coût total reste le même que dans le cinéma original, mais les coûts individuels par enfant sont légèrement différents en raison des différences de prix dans les deux cinémas.
Exercice 7 : les téléphones mobiles
Calculons le prix de retour pour chaque tarif :
**TARIF A**
* Prix initial du téléphone : 49 €
* Frais d’abonnement mensuel : 26 €/mois
* Durée de l’abonnement : 24 mois
* Coût total de l’abonnement : 26 €/mois × 24 mois = 624 €
* Coût total du tarif : 49 € (prix initial) + 624 € (abonnement) = 673 €
Prix de retour (coût par mois) : 673 € ÷ 24 mois = 28,04 €/mois
**TARIF B**
* Prix initial du téléphone : 149 €
* Frais d’abonnement mensuel : 37 €/mois
* Durée de l’abonnement : 12 mois
* Coût total de l’abonnement : 37 €/mois × 12 mois = 444 €
* Coût total du tarif : 149 € (prix initial) + 444 € (abonnement) = 593 €
Prix de retour (coût par mois) : 593 € ÷ 12 mois = 49,42 €/mois
**TARIF C**
* Prix initial du téléphone : 399 €
* Pas de frais d’abonnement
* Coût total du tarif : 399 € (prix initial)
Prix de retour (coût par mois) : N/A (pas d’abonnement mensuel)
En comparant les trois tarifs, on constate que :
* LE TARIF A est le plus cher, avec un prix de retour de 28,04 €/mois.
* LE TARIF B est le deuxième plus cher, avec un prix de retour de 49,42 €/mois.
* LE TARIF C est l’option la plus économique, avec un paiement unique de 399 € et sans frais d’abonnement mensuel.
Le TARIF C est donc l’option la plus intéressante.
Exercice 8 :
a. Pour trouver quelle sauterelle atteindra l’extrémité du plateau, nous devons calculer la distance qu’elle parcourra au total.
La première sauterelle fait des sauts de 5 cm, la distance totale qu’elle parcourra est donc de :
5 cm + 5 cm + … (jusqu’à ce qu’il atteigne le bout de la planche)
La deuxième sauterelle fait des sauts de 3 cm, la distance totale qu’elle parcourra est donc :
3 cm + 3 cm + … (jusqu’à ce qu’il atteigne l’extrémité du plateau)
La planche mesure 2 mètres de long, ce qui équivaut à 200 cm. Puisque les deux sauterelles partent du même point, elles arriveront au bout du plateau en même temps.
La première sauterelle arrivera en bout de plateau lorsqu’elle aura réalisé :
200 cm ÷ 5 cm = 40 sauts
La deuxième sauterelle arrivera en fin de plateau lorsqu’elle aura réalisé :
200 cm ÷ 3 cm = 66,67 sauts (environ)
Puisque 66,67 sauts n’est pas un nombre entier, nous ne pouvons pas déterminer exactement quelle sauterelle atteindra la fin du plateau en premier. On peut cependant conclure que la deuxième sauterelle mettra plus de sauts pour arriver au bout du plateau que la première sauterelle.
b. Pour trouver le nombre minimum de sauts nécessaires à chaque sauterelle pour atteindre l’extrémité du plateau, on peut calculer la distance totale qu’ils doivent parcourir :
Pour la première sauterelle : 200 cm
Pour la deuxième sauterelle : 200 cm
La première sauterelle devra réaliser :
200 cm ÷ 5 cm = 40 sauts
La deuxième sauterelle devra réaliser :
200 cm ÷ 3 cm = 66,67 sauts (environ)
Ainsi, les deux sauterelles devront faire au moins 40 sauts pour atteindre le bout du plateau.

Exercice 16 : opérations
Calculer mentalement :
a. 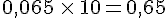 b. 79,2x 1 000=79 200 c. 71,47 x 100=7 147
b. 79,2x 1 000=79 200 c. 71,47 x 100=7 147
d. 0,34 x 1 000 = 340 e. 87 x 100 = 8 700
f. 934 x 10 =9 340 g. 0,001 x 1 000 = 1 h. 0,05 x 10 000 = 500.
Exercice 17 :
Convertir les longueurs suivantes :
a. 84 km=84 000 m. b. 84 hm= 8 400 m. c. 84 mm=0,084 m. d. 84 dm= 8,4 m.
e. 3,1 hm = 0,31 km. f. 3,1 dam = 31 m. g. 3,1 m = 0,031 hm.
Exercice 18 :
Calculer mentalement les additions suivantes :
a. 5,6 + 7,2=12,8 b. 2,2 + 6,3 = 8,5 c. 3,5 + 7,1=10,6 d. 6,3 + 7,6 = 13,9
e. 9+ 3,5 = 12,5 f. 2,9 + 6,5 = 9,4 g. 5,8 + 9,3 = 15,1
Exercice 19 :
Calculer mentalement les soustractions suivantes :
a. 5,5 – 4,3 = 1,2 b. 4,6 – 0,5 = 4,1 c. 2,8 – 2,1 = 0,7
d. 6,7 – 0,5 = 6,2 e. 3,8 – 3,5 = 0,3 f. 4,6 – 2,8 = 1,8 g. 9,7 – 5,9 = 3,8.
Exercice 20 :
Placer la virgule dans le nombre écrit en caractère gras pour que l’égalité soit vraie.
Exercice 21 :
Poser les multiplications suivantes et calculer.
Exercice 22 :
Recopier puis placer correctement la virgule en rouge dans le nombres souligné :
1/ 75,315×4,83=363,771 45
2/ 1,08×471,591=509,318 38
3/ 54,026×2,47=133,444 22
4/ 0,861 597×552,5=476,032 342 5
Exercice 23:
Poser la multiplication pour calculer :
• le produit de 5,4 par 60,9 : 5,4×60,9 =328,86.
• le produit de 7,536 par 8,6 : 7,536 x 8,6 = 64,809 6.
Exercice 24 :
Recopier puis donner le résultat :
1/ 45×10=450
2/ 57,6×0,1=5,76
3/ 5,69×0,001= 0,005 69
4/ 8,67×1000=8 670
5/ 12,1×10 =121
6/ 0,089×100=8,9
7/ 0,089×100=8,9
8/ 100×0,0001= 0,01
Exercice 25 :
Calculer les produits suivants en faisant des regroupements astucieux :
1/ A=4×3,98×25×10 = 4x25x3,98×10=100×3,98×10=3 980.
2/ B=8×7,1234×25 = 8x25x7,1234=2x100x7,1234=1 424,68.
3/ Donner la propriété fondamentale du cours qui vous a permis d’effectuer ces calculs.
Propriété : la multiplication est commutative.
Exercice 26 :
Effectuer les divisions décimales suivantes afin d’en trouver le quotient décimal exact.
a. 17,22 : 3 = 5,74;
b. 0,126 : 9 = 0,014;
c. 47,5 : 4 = 11,875;
d. 5,46 : 12 = 0,455.
Exercice 27 :
1/ Pour un concert, dix-mille billets ont été vendus.
Le billet coûte 11 € 20. Quelle est la recette ?
11,20×10 000 = 112 000 €
2/ Un train de dix wagons transporte des voitures dont le prix à l’unité est de 0,014850 millions d’euros.
Il y a dix voitures par wagon.
Quelle somme d’argent représente l’ensemble des voitures contenues dans ce train ?
10x10x0,014850=1,485 millions d’euros.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «problèmes sur les 4 opérations : corrigé des exercices de maths en 6ème en PDF.» au format PDF.
Ressources de sixième
Cours de sixième
D'autres cours et exercices à consulter
🤖 Exercices IA Interactifs ✨

Des milliers d'exercices interactifs conformes aux programmes officiels. Apprenez, pratiquez et progressez à votre rythme.
Exercices interactifsL'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.