Symétrie axiale et centre de symétrie : cours de maths en 6ème en PDF.
I. Figures symétriques
Deux figures sont symétriques par rapport à une droite si elles se superposent par pliage le long de cette droite.
Cette droite est appelée l’axe de symétrie.
II. Symétrique d’un point.
1.Définition du symétrique.
Le symétrique d’un point A par rapport à une droite (d) est le point A’, tel que la droite (d)soit la médiatrice du segment [AA’] (c’est-à-dire tel que (d) soit la perpendiculaire au segment [AA’] en son milieu).
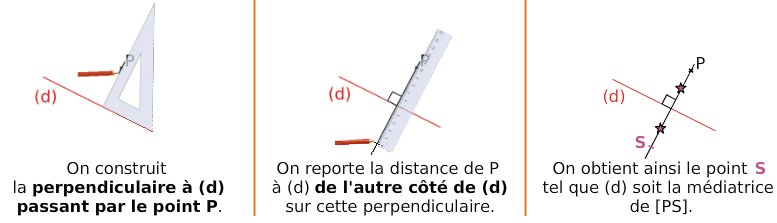
2. Construction du symétrique avec l’équerre et la règle graduée.
3. Construction du symétrique avec le compas.
III. Propriétés de la symétrie axiale
Le symétrique d’une droite par rapport à un axe est une droite.
La symétrie axiale conserve l’alignement.
Remarque :
Le symétrique du milieu d’un segment est le milieu du segment symétrique.
Le symétrique d’un cercle par rapport à un axe est un cercle de même rayon. Les centres des cercles sont symétrique par rapport à cet axe.
Exemples :
Pour construire le symétrique d’une figure complexe, on la décompose en figures usuelles et on construit le symétrique de chacune d’elles.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «symétrie axiale et centre de symétrie : cours de maths en 6ème en PDF.» au format PDF.
D'autres cours et exercices à consulter
- Périmètre et aires : cours de maths en 6ème en PDF.
- Médiatrice d’un segment : cours de maths en 6ème en PDF.
- Droites parallèles et perpendiculaires : cours de maths en 6ème en PDF.
- La division et les problèmes : cours de maths en 6ème en PDF.
- Les nombres décimaux : cours de maths en 6ème en PDF.
- Les 4 opérations avec l’addition, la soustraction, la multiplication et la division : cours de maths en 6ème en PDF.
- Fractions : cours de maths en 6ème en PDF.
- Proportionnalité et pourcentages : cours de maths en 6ème en PDF.
