Droites parallèles et perpendiculaires : cours de maths en 6ème en PDF.
Mis à jour le 22 avril 2025
I. Droites parallèles :
1.Définition :
Deux droites (d) et (d’) sont dites « parallèles » si elles n’ont pas de point d’intersection,
même en les prolongeant indéfiniment.
On note : (d) // (d’)
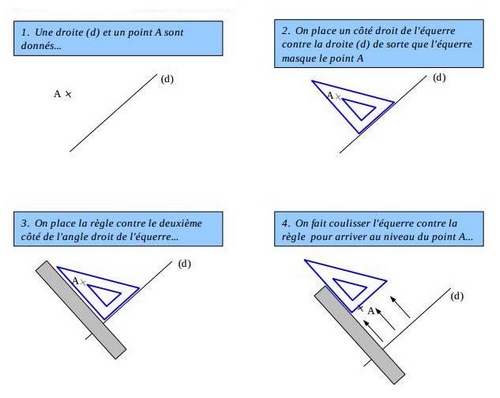
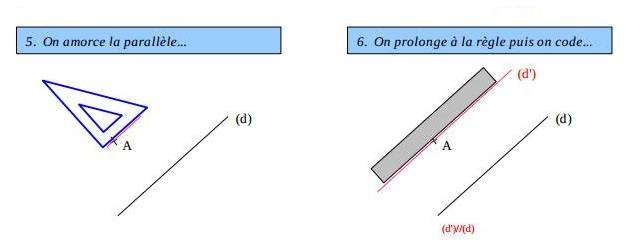
2.Méthode de construction de la parallèle à une droite passant par un point donné :
Remarques :
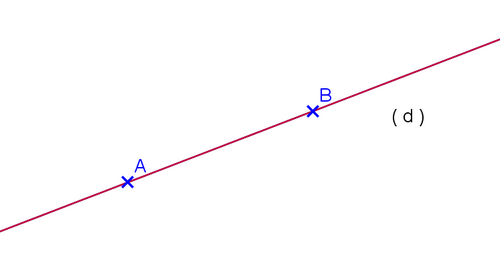
- Les droites (d) et (AB) se superposent ;
- On dit qu’elles sont confondues.
II. Droites perpendiculaires :
1. Définition :
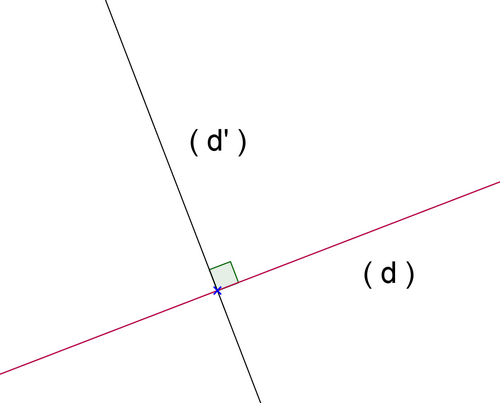
Deux droites (d) et (d’) sont dites « perpendiculaires » si elles se coupent en formant un angle droit (on le vérifie avec une équerre).
On note : 
.
Remarques :
- Deux droites perpendiculaires sont sécantes;
- Deux droites sécantes ne sont pas toujours perpendiculaires.
2. Méthode de construction d’une perpendiculaire à une droite donnée :
III. Propriétés des figures formées par trois droites :
1. Propriété 1 (admise) :
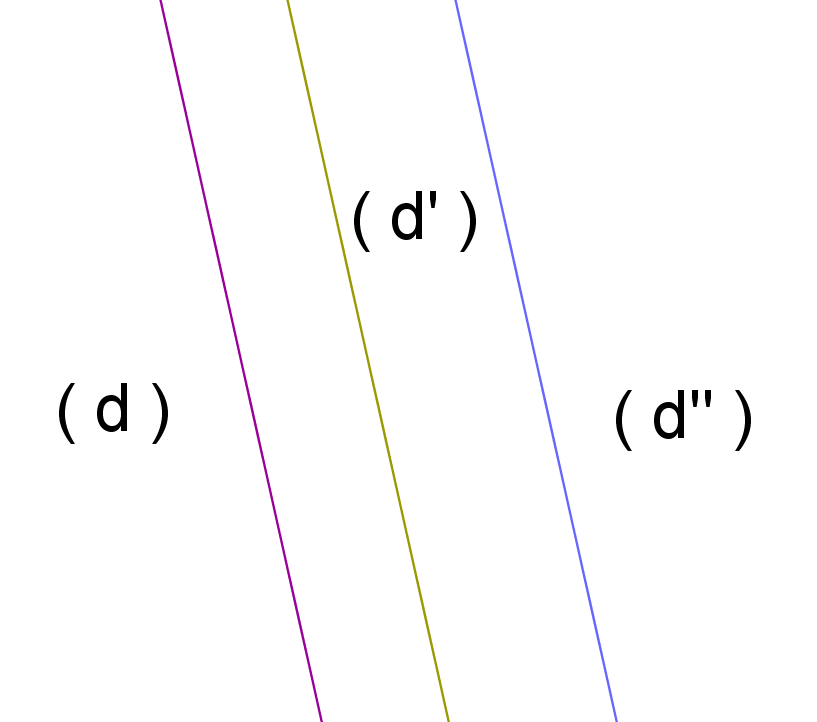
Si deux droites sont parallèles à une même troisième droite, alors ces deux droites sont parallèles entre elles.
Preuve :
On sait que : (d) est parallèle à (d ») et que (d’) est parallèle à (d »)
Conclusion :
Les droites (d) et (d’) sont parallèles.
2. Propriété 2 (admise) :
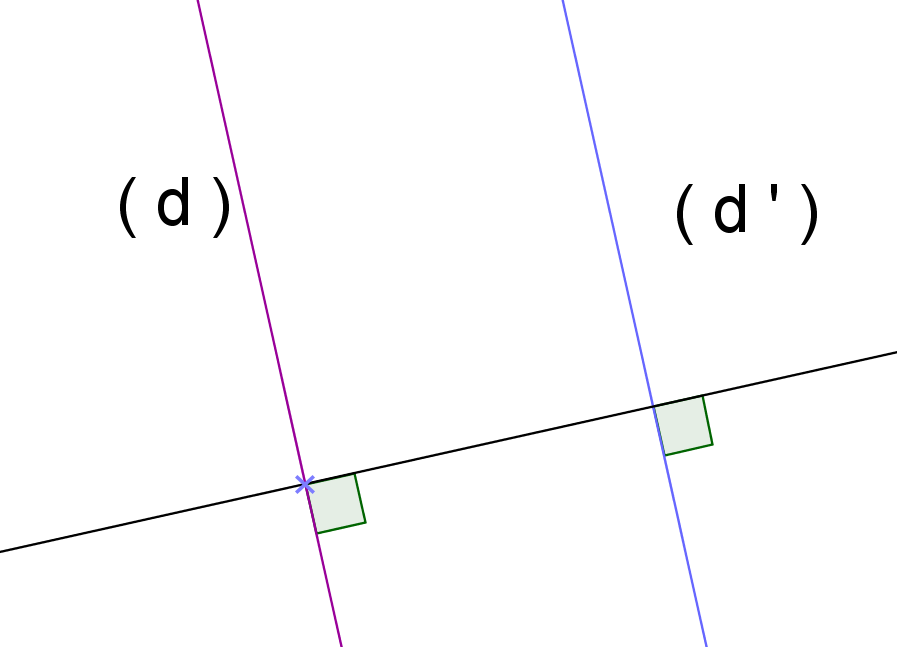
Si deux droites sont perpendiculaires à une même troisième droite, alors ces deux droites sont parallèles entre elles.
Preuve :
On sait que : (d) est perpendiculaire à (d ») et que (d’) est perpendiculaire à (d »).
Conclusion :
Les droites (d) et (d’) sont parallèles.
Propriété 3 (admise) :
Si deux droites sont parallèles et si une troisième droite est perpendiculaire à l’une, alors elle est perpendiculaire à l’autre.
Preuve :
On sait que : (d) est parallèle à (d’)
et que (d ») est perpendiculaire à (d).
.png)
Conclusion :
Les droites (d ») et (d’) sont perpendiculaires.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «droites parallèles et perpendiculaires : cours de maths en 6ème en PDF.» au format PDF.
Ressources de sixième
Cours de sixième
Exercices de sixième
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.
