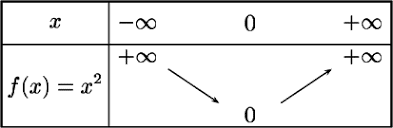
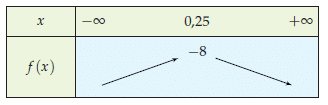
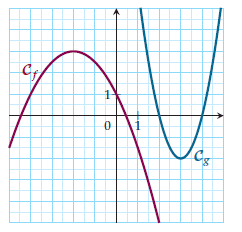
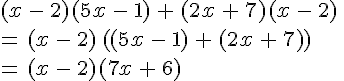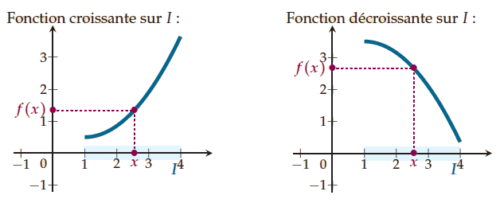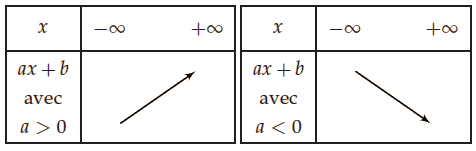Tous les cours de maths en 2de pour les élèves de seconde.

Position relative d’une droite et d’un plan dans l’espace : cours de maths en 2de en PDF.

2 décembre 2024 par webmaster

La géométrie dans l’espace à travers un cours de maths en 2de sur les solides usuels (parallélépipède rectangle, pyramide, cône de révolution, cylindre de révolution, sphère et boule). Dans cette leçon en seconde, nous étudierons la position relative de droites et de plans dans l’espace. Connaissances du collège nécessaires à ce chapitre Connaître les formules d’aires des … Lire la suite

Généralités sur les fonctions et fonctions usuelles : cours de maths en 2de en PDF.

2 décembre 2024 par webmaster

Les généralités sur les fonction numériques et les fonctions usuelles à travers un cours de maths en 2de. Dans cette leçon, nous étudierons les fonctions carrée, affine, linéaire, inverse et racine carrée ainsi que leur courbe représentatives. L’élève de vra être capable de calcul une image ou de déterminer un antécédent pas le calcul ou … Lire la suite

Généralités sur les fonctions numériques : cours de maths en 2de en PDF.

30 novembre 2024 par webmaster

Les généralités sur les fonctions numériques dans un cours de maths en 2de où nous étudierons les opérations sur les fonctions ainsi que les égalités. dans cette leçon en seconde, nous aborderons le sens de variation d’une somme, produit et composée de fonctions numériques. I. Opérations algébriques sur les fonctions : 1. Egalité : Définition … Lire la suite

Fonctions polynômes du second degré : cours de maths en 2de en PDF.

27 novembre 2024 par webmaster

Les fonctions polynômes du second degré dans un cours de maths en 2de.

Cette leçon en seconde traite de la forme canonique, de l’étude d’une fonction trinôme et de sa représentation graphique.
Connaissances du collège nécessaires à ce chapitre

Développer une expression littérale;
Reconnaître un axe de symétrie;
Additionner des fractions;
Multiplier des fractions.

1. Forme canonique

Définition : Fonction polynôme de degré 2

Soit a, b, c trois nombres réels avec $a\neq0$ .
On appelle fonction polynôme de degré 2 toute fonction P définie sur $\mathbb{R}$ pouvant être exprimée sous la forme : $P(x)\,=\,ax^2\,+\,bx\,+\,c$ .
On parle aussi de fonction trinôme.

Propriété

Soit P une fonction polynôme du second degré exprimée sous la forme $P(x)\,=\,ax^2\,+\,bx\,+\,c$ .
Il existe deux nombres réels α et β permettant d’écrire P sous le forme :
$P(x)\,=\,a(x\,-\,\alpha\,)^2\,+\beta$ .
Cette forme s’appelle forme canonique.

2. Étude d’une fonction trinôme

Propriété : sens de variations.

Soit a, α, β trois nombres réels et f une fonction polynôme de degré 2 définie sur $\mathbb{R}$ par sa forme canonique $f(x)\,=\,a(x\,-\,\alpha\,)^2\,+\beta$ .
Le sens de variation d’une fonction dépend du signe de a.

Extremum d’une fonction.

Soit a, $\alpha$ , $\beta$ trois nombres réels.
f une fonction polynôme de degré 2 définie sur $\mathbb{R}$ par sa forme canonique
$f\,(x)\,=\,a\,(x\,-\alpha\,)^2\,+\,\beta$ .
Sur R, la fonction f admet $\beta$ comme extremum. Il est atteint pour x = α.
C’est un maximum si $\alpha$ est négatif.
C’est un minimum si $\alpha$ est positif.

Signe d’une fonction.

Soit a, $\alpha$ , $\beta$ trois nombres réels et f une fonction polynôme de degré 2 définie sur $\mathbb{R}$ par sa
forme canonique $f\,(x)\,=\,a\,(x\,-\alpha\,)^2\,+\,\beta$ .
Le signe d’une fonction trinôme dépend du signe de a et du signe de $\beta$ .
Si a < 0 et $\beta$ $\leq\,$ 0, alors la fonction est toujours négative.
Si a > 0 et $\beta$ $\geq\,$ 0 alors la fonction est toujours positive.
Dans les autres cas,
la fonction change de signe sur l’intervalle $]\,-\infty;\alpha[$ ;
la fonction change à nouveau de signe sur l’intervalle $]\alpha\,;+\infty[$ .

Méthode : étudier une fonction trinôme du second degré.

Exemple:

On considère la fonction f définie sur $\mathbb{R}$ par $f\,(x)\,=\,-2(x\,-\,0,\,25)^2\,-\,8$ .
Déterminer :
1) son sens de variation ;
2) son extremum;
3) le signe de la fonction.

Correction :

Dans le cas de la fonction f :
• α = 0, 25 • $\beta$ = −8 • a = −2
1) a est négatif donc la fonction f est croissante sur $]-\infty;\,0,\,25[$ et décroissante sinon.
2) Elle admet un maximum en x = $\alpha$ = 0, 25. Il vaut f (0, 25) = −8.

3) La fonction f est négative sur $\mathbb{R}$ .

3. Représentation graphique de fonctions

Définition :

La courbe représentative d’une fonction trinôme est une parabole.

Propriété :

Soit a, α, β trois nombres réels et f une fonction trinôme définie sur $\mathbb{R}$ par sa forme canonique
$f\,(x)\,=\,a\,(x\,-\alpha\,)^2\,+\,\beta$ .La courbe représentative de cette fonction est une parabole qui admet un axe de symétrie : la droite d’équation x = $\alpha$ .

Exemple :

Tracer les courbes représentatives des fonctions suivantes :
• $f\,(x)\,=\,-0,\,5(x\,+\,2)^2\,+\,3$
• $g(x)\,=\,2(x\,-3)^2\,-\,2$
Donner leurs sens de variations et leur éventuel extremum.

Correction

La fonction f :
• est croissante sur ]− $\infty$ ;−2[ ;
• est décroissante sur ]−2;+ $\infty$ [ ;
• elle admet un maximum en −2 qui vaut 3.

La fonction g :
• est décroissante sur ]− $\infty$ ; 3[ ;
• est croissante sur ]3;+ $\infty$ [ ;
• elle admet un minimum en 3 qui vaut −2.

Les systèmes d’équations : cours de maths en 2de en PDF.

18 novembre 2024 par webmaster

Résolution de systèmes de deux équations à deux inconnues : méthode par substitution et par combinaison linéaire (dite méthode par addition) à travers un cours de maths en 2de. Résolution de problème et traduction mathématique d’un énoncé). 0. Introduction : Problème : Je dispose de deux récipients A et B dont la contenance est exprimée … Lire la suite

Nombres entiers et rationnels et calcul du PGCD : cours de maths en 2de en PDF.

11 novembre 2024 par webmaster

L’arithmétique et les ensembles de nombres à travers un cours de maths en 2de sur les nombres entiers et rationnels en seconde. Cette leçon fait intervenir la notion de multiple, diviseur, plus grand diviseur et le calcul de pgcd avec la méthode classique, l’algorithme des différences, l’algorithme d’Euclide et également les ensembles de nombres pour une … Lire la suite

Racine carrée : cours de maths en 2de en PDF.

6 novembre 2024 par webmaster

La racine carrée d’un nombre à travers un cours de maths en 2de. Nous allons aborder la définition ainsi que toutes les formules de calculs à l’aide des racines carrées en classe de seconde. I. Racine carrée d’un nombre positif : Définition : La racine carrée d’un nombre positif est le nombre positif noté dont le … Lire la suite

Factorisation et étude de signe : cours de maths en 2de en PDF.

23 octobre 2024 par webmaster

La factorisation et l’étude de signes dans un cours de maths en 2de où nous étudierons le signe d’une fonction affine et son tableau de variation puis la factorisation d’une expression littérale.Dans un second temps, nous traiterons dans cette leçon en seconde, le signe du produit de deux fonctions affines et enfin, le signe d’une fonction homographique.

L’élève devra avoir acquis les pré-requis suivants afin de pouvoir aborder ce chapitre :

Résoudre

une équation de type ax + b = 0;
une équation produit;
une inéquation de type ax + b > 0;
représenter les solutions sur un axe gradué

Factoriser

avec les identités remarquables;
avec un facteur commun évident.

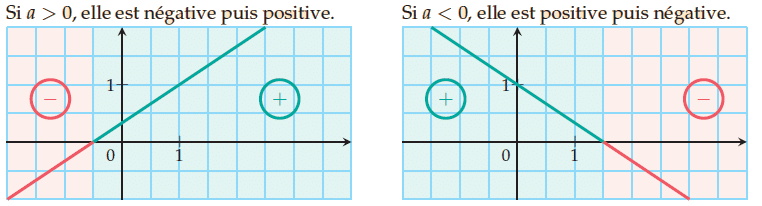
I. Signe d’une fonction affine

Propriété :

Soit a et b deux nombres réels avec $a\neq0$ .
La fonction affine définie sur $\mathbb{R}$ par f (x) = ax + b s’annule et change de signe une fois dans
son domaine de définition pour $x\,=\,-\frac{b}{a}$ .

Preuve :

Soit f une fonction affine définie sur $\mathbb{R}$ par f (x) = ax + b avec a $a\neq0$ .
f (x) = 0 implique ax + b = 0 soit ax = −b et $x=-\frac{b}{a}$ .
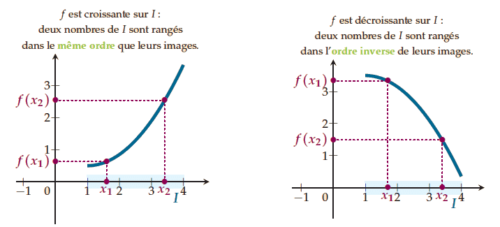
Si a > 0, la fonction f est croissante.
$\star\,$ Pour $x\,<\,-\frac{b}{a}$ , $f(x)<f(-\frac{b}{a})$ .Or $f(-\frac{b}{a})=0$ donc .

$\star\,$ Pour $x\,>\,-\frac{b}{a}$ , $f(x)>f(-\frac{b}{a})$ .Or $f(-\frac{b}{a})=0$ donc .

Donc f est négative sur $]-\infty;-\frac{b}{a}[$ puis positive sur $]-\frac{b}{a};+\infty[$ .
Si a < 0, la fonction f est décroissante.

$\star\,$ Pour $x\,<\,-\frac{b}{a}$ , $f(x)>f(-\frac{b}{a})$ .Or $f(-\frac{b}{a})=0$ donc .

$\star\,$ Pour $x\,>\,-\frac{b}{a}$ , $f(x)<f(-\frac{b}{a})$ .Or $f(-\frac{b}{a})=0$ donc .

Donc f est positive sur $]-\infty;-\frac{b}{a}[$ puis négative $]-\frac{b}{a};+\infty[$ .

1.Méthode : dresser le tableau de signes d’une fonction affine.

Tableau de signe:

Le tableau de signes d’une fonction affine comporte deux lignes.
Sur la première ligne on indique les bornes du domaine de définition de la fonction et
la valeur qui annule la fonction.
Sur la deuxième ligne, par des pointillés verticaux sous la valeur qui annule,
on crée deux cases dans lesquelles on indique le signe de la fonction.

Exemple :

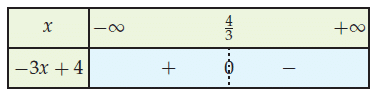
Dresser le tableau de signes de la fonction g définie sur $\mathbb{R}$ par $g\,:\,x\,\mapsto \,-3x\,+\,4.$

Le coefficient directeur,−3, est négatif donc g est décroissante.
Recherche de la valeur qui annule :
−3x + 4 = 0 soit $x\,=\,\frac{-4}{-3}=\frac{4}{3}$ .

2. Factorisation

Remarque :

En classe de seconde, on a déjà des outils pour factoriser une grande partie
des polynômes de degré 2. D’autres outils seront étudiés en Première.

En Terminale, dans certaines séries, toutes les expressions seront factorisables.

3. Méthode : factoriser une expression littérale.

Méthode :

Soit a, b, k trois nombres réels.
$\star\,$ Si un facteur est apparent, on utilise :

.
$\star\,$ Si un facteur n’est pas apparent, on utilise les identités remarquables :

Exemple :

Factoriser les expressions suivantes :
1) 4ac − 6ab
2) (x − 2)(5x − 1) + (2x + 7)(x − 2)
3) $x^2-\,6x\,+\,9$
4) $36x^2-\,81$

1) $4ac\,-\,6ab\,=\,2a(2c\,-\,3b)$
2)

$(x\,-\,2)(5x\,-\,1)\,+\,(2x\,+\,7)(x\,-\,2)\,\\=\,(x\,-\,2)\,((5x\,-\,1)\,+\,(2x\,+\,7))\,\\=\,(x\,-\,2)(7x\,+\,6)$

3) $x^2-\,6x\,+\,9\,=\,x^2\,-\,2\,\times \,x\,\times \,3\,+\,32\,=\,(x\,-\,3)^2$
4) $36x^2\,-81\,=\,(6x)^2-\,9^2\,=\,(6x\,+\,9)(6x\,-\,9)$ .

II. Signe du produit de deux fonctions affines

1. Méthode : étudier le signe du produit de deux fonctions affines.

Méthode :

Pour déterminer le signe du produit de deux fonctions affines, on construit un tableau de
signes à 4 lignes.
1) La 1e ligne indique les bornes de l’ensemble de définition
et les valeurs qui annulent le produit des deux fonctions affines.
2) Les 2e et 3e lignes indiquent le signe de chacune des deux fonctions affines.
3) La 4e ligne se remplit avec la règle des signes du produit de deux nombres relatifs :
a) des facteurs de même signe donnent un produit positif ;
b) des facteurs de signes contraires donnent un produit négatif.

Exemple :

Résoudre l’inéquation $(3x\,+\,4)(-2x\,+\,6)\,\leq\,\,0$ .
On étudie le signe de la fonction h définie sur $\mathbb{R}$ par h(x) = (3x + 4)(−2x + 6).
Recherche des valeurs qui annulent :
$\star\,$ 3x + 4 = 0 implique $x\,=-\frac{4}{3}$ .
$\star\,$ −2x + 6 = 0 implique x = 3.

Les solutions de cette inéquation sont les nombres de l’ensemble $[3;+\infty[$ .;

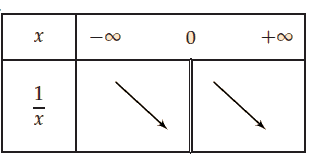
III. Signe d’une fonction homographique

Définition : fonction homographique.

On appelle fonction homographique toute fonction h qui peut s’écrire comme quotient de
fonctions affines. Soit a, b, c, d quatre réels tels que $ad-\,bc\,\neq0$ et $c\neq0$ : $h(x)\,=\frac{ax\,+\,b}{cx\,+\,d}.$

Propriété :

Une fonction homographique est définie sur $\mathbb{R}$ privé de la valeur qui annule son dénominateur
dite « valeur interdite ».
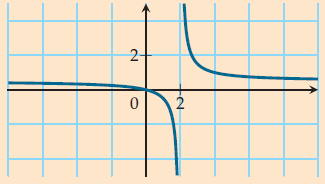
Sa courbe représentative est une hyperbole qui comporte deux branches disjointes.

1.Méthode : donner le domaine de définition d’une fonction homographique.

Méthode :

Pour identifier ce domaine de définition, il suffit de trouver la valeur interdite.

Exemple :

Quel est le domaine de définition de la fonction f définie par $f\,(x)\,=\frac{5x\,+\,4}{3x\,-\,7}$ ?

Recherche de la valeur interdite : $3x\,-\,7\,=\,0\,\Leftrightarrow\,x\,=\frac{7}{3}$ .
Le domaine de définition de la fonction f définie par $f\,(x)\,=\frac{5x\,+\,4}{3x\,-\,7}$ est $\mathbb{R}-\,\,\{\,\frac{7}{3}\,\,\}$ .

2.Méthode : donner le tableau de signes d’une fonction homographique.

Méthode :

La méthode est similaire à celle du produit de deux fonctions affines.
La valeur qui annule le dénominateur ne faisant pas partie du domaine de définition de la
fonction doit être indiquée par une double barre.

Exemple :

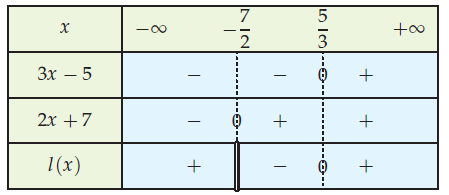
Résoudre l’inéquation $\frac{3x\,-\,5}{2x\,+\,7}>\,0.$

On étudie le signe de la fonction l définie par $l(x)=\,\frac{3x\,-\,5}{2x\,+\,7}$ .

$\star\,$ Recherche de la valeur interdite :
$2x\,+\,7\,\neq\,0$ implique $x=-\frac{7}{2}$ donc l est définie sur R \ $\,\{\,-\frac{7}{2}\,\,\}$ .
$\star\,$ Recherche de la valeur qui annule l :
3x − 5 = 0 implique $x=\frac{5}{3}$ .

$\star\,$ Comparaison des valeurs trouvées pour les ranger sur la 1re ligne du tableau : $-\frac{7}{2}<\frac{5}{3}$ .

Les solutions de l’inéquation $\frac{3x\,-\,5}{2x\,+\,7}>\,0$ sont les nombres de l’ensemble $]-\infty;-\frac{7}{2}[\cup\,]\frac{5}{3};+\infty[$ .

Variations de fonctions et extremums : cours de maths en 2de en PDF.

22 octobre 2024 par webmaster

Les variations de fonctions et les extremums à travers un cours de maths en 2de avec la croissance et décroissance d’une fonction ainsi que le tableau de variation. Nous étudierons, dans cette leçon en seconde, l’aspect algébrique puis l’aspect graphique de l’étude des variations.
Les connaissances de collège nécessaires pour aborder cette fiche sont les suivantes :

Calculer l’image d’un nombre par une fonction;
Lire une image par une fonction sur un graphique;
Reconnaître une fonction affine;
Connaître les effets des opérations sur l’ordre des nombres.

I. Point de vue graphique

1. Fonction croissante, décroissante, constante

Définition :

On dit que f est croissante sur un intervalle I lorsque si x augmente sur I alors f (x) augmente.
On dit que f est décroissante sur un intervalle I lorsque si x augmente sur I alors f (x) diminue.

Définition :

Soit une fonction et C_f sa courbe représentative dans un repère.
On voit sur un graphique que :

f est croissante sur I lorsque Cf «monte » sur I ;
f est décroissante sur I lorsque Cf « descend » sur I.
Lorsque sur un intervalle, la courbe est horizontale,on dit que la fonction est constante. On considère qu’elle est à la fois croissante et décroissante.
Une fonction qui ne change pas de sens de variations sur un intervalle est dite monotone sur cet intervalle.

2. Maximum et minimum d’une fonction

Définition :

Sur un intervalle I,

le maximum d’une fonction f est la plus grande des valeurs prises par f (x) ;
le minimum d’une fonction f est la plus petite des valeurs prises par f (x).

3. Tableau de variation d’une fonction et variations

Définition :

Un tableau de variations regroupe toutes les informations concernant les variations d’une
fonction numérique sur son domaine de définition.

Méthode : dresser un tableau de variation

Un tableau de variations comporte deux lignes.

Aux extrémités de la première ligne, on trouve les bornes du domaine de définition de la fonction.
Entre les bornes, on place d’éventuelles valeurs particulières.
Le sens de variation de la fonction est indiqué sur la deuxième ligne par une ou plusieurs flèches sur les intervalles où elle est monotone : pour croissante et pour décroissante.
Les valeurs pour lesquelles la fonction n’est pas définie sont indiquées par une double
barre verticale sur la deuxième ligne.
On indique au bout des flèches les images des valeurs de la première ligne.

Exemple :

Dresser le tableau de variations de la fonction définie sur [−2; 2] par la courbe ci-dessous.

Voici le tableau de variation correspondant :

II. Point de vue algébrique

1.Variation d’une fonction

Définition : croissance, décroissance sur un intervalle.

Soit f une fonction définie sur un intervalle I et x_1 et x_2 deux nombres de I.
Si $x_1\leq\,\,x_2$ implique $f(x_1)\leq\,\,f(x_2)$ alors f est dite croissante sur I.
Si $x_1\,\geq\,\,x_2$ implique $f(x_1)\,\geq\,\,f(x_2)$ alors f est dite décroissante sur I.

Propriété : tableau de variations des fonctions affines et de la fonction inverse.

Le sens de variation de la fonction affine dépend du signe de a.
La fonction inverse est décroissante sur $R^{-*}$ et sur $R^{+*}$ .

Tableau de variation des fonctions affines

Démonstration :
On considère une fonction f tel que f (x) = ax + b et deux nombres tels que .
Si $a<0;\,ax_1>ax_2$ et $f(x_1)\,>\,f(x_2)$ . La fonction f est donc décroissante sur R.
Si $a<0;\,ax_1<ax_2$ et $f(x_1)<\,f(x_2)$ . La fonction f est donc croissante sur R.

Tableau de variation de la fonction inverse

2. Maximum et minimum d’une fonction

Définition : maximum, minimum et extremum d’une fonction

Dire que f admet un maximum en a sur l’intervalle I signifie que :

Il existe un réel M tel que pour tout x dans I : $f(x)\leq\,\,M$ et M=f(a) ;

Dire que f admet un minimum en b sur l’intervalle I signifie que :
Il existe un réel m tel que pour tout x dans I : $f(x)\,\geq\,\,m$ et ;
Un extremum est le terme générique pour désigner un maximum ou un minimum.

Propriété : tableau de variations de la fonction carrée.

La fonction carrée est décroissante sur $R^{-}$ et croissante sur $R^{+}$ .
Elle admet, sur , un minimum en 0.

Equations, inéquations et résolution graphique : cours de maths en 2de en PDF.

21 octobre 2024 par webmaster

La résolution d’équations et d’inéquations dans un cours de maths en 2de où nous résolvons des équations par le calcul puis par la méthode graphique. Connaissances du collège nécessaires à ce chapitre. Vérifier qu’un nombre est solution d’une équation; Vérifier qu’un nombre est solution d’une inéquation; Résoudre des équations simples; Résoudre des inéquations simples. 0. … Lire la suite