cours maths 2de

Rappels du collège sur les ensembles de nombres : cours de maths en 2de en PDF.

par
Aidez-nous à améliorer cette page en signalant une erreur Signaler une erreur Aidez-nous à améliorer cette page en signalant une erreur
 Une synthèse à travers un cours de maths en 2de sur les différentes notions abordées au collège comme les ensembles de nombres, l’arithmétique et la décomposition en facteurs premiers ainsi que les calculs avec les nombres relatifs, les fractions et les puissances. Il s’agit de définir ce que sont la troncature, les arrondis, les valeurs par défaut et par excès d’un nombre écris sous forme décimale. On y introduit par exemple la notation en écriture scientifique d’un nombre.

I. La notation scientifique d’un nombre

Définition :
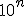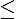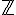Elle est de la forme a x 10^n avec 1\leq\,a<10, avec n un entier relatif (n € \mathbb{Z})

Exemple :

12 345  = 1.2345 x 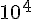10^4

0.0987  = 9.87 x 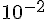10^{-2^}

II. Les nombres décimaux (purs).

Définition :

L’écriture décimale d’un nombre se compose d’une partie entière et d’une partie décimale séparéespar une virgule (« , »).

Exemple :

1,5 sa partie entière vaut 1 et sa partie décimale vaut 5

3,14 Sa partie entière vaut 3 et sa partie décimale vaut 14

Règle :

Règle des 0 non significatifs avant de regarder la partie entière et la partie décimale d’un nombre

A noter qu’on préfère retirer tous les 0 non significatifs(= inutiles) qui précèdent l’écriture d’un nombre, à gauche, et tous les 0 non significatifs qui terminent le nombre à droite.

Exemples:

à gauche des 0 inutiles

001234,56789 s’écrira de préférence 1234,456789 mais par contre peut s’écrire 1234,5678900

à droite des 0 inutiles

10,00 s’écrira de préférence 10 mais peut s’écrire 10,000000

III.LES NOMBRES RATIONNELS

Définition :

Que dire des nombre qui sont le rapport de deux entiers et de leur écriture décimale?3/2 = 1,5 et c’est simple

Mais 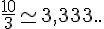\frac{10}{3}\simeq3,333...

Pour certains nombres il nous est donc impossible de décrire entièrement leur partie décimale.

IV.LES NOMBRES REELS

Définition :

Que penser cette fois ci de l’écriture du nombre 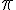\piqui n’est pas égale à 3,14159265 ?

On s’approche avec une certaine précision de sa valeur réelle, mais il nous est impossible d’écrire entièrement sa partie décimale.

On dit qu’on l’a soit tronqué, soit arrondi…avec une certaine précision!
Pour pouvoir écrire, du moins en partie, ces nombres on utilise ce que l’on appelle une troncature ou un arrondi ou encore une valeur approchée.

Par la suite on appellera « nombre décimal » tout nombre (qu’il soit réel, rationnel ou décimal pur) écris avec un nombre fini de chiffres après la virgule.

V.La Troncature

Définition :

La troncature à l’unité d’un nombre décimal positif est sa partie entière.

On peut l’obtenir en supprimant tous les chiffres à la droite de la virgule.

Exemple :

La troncature à l’unité de 12,637 est 12
On définit aussi, si on veut plus de précision :

-La troncature au dixième:

Exemple:

La troncature au dixième de 12,637 est 12,6

-La troncature au centième, etc.:

Exemples:

La troncature au centième de 12,637 est 12,63

La troncature au millième de 12,637 est 12,637 lui-même

VI. L’arrondi.

Définition :

L’arrondi à l’unité d’un nombre décimal est le nombre entier le plus proche de celui-ci.

Exemple :

– L’arrondi à l’unité du nombre 56,8 est le nombre entier 57

Par convention, l’arrondi à l’unité du nombre 53,5 est 54

Pour des nombres positifs :

Si le chiffre après la virgule est inférieur à 5 (c’est à dire appartient à {0;1;2;3;4}),

on arrondit à l’entier inférieur.

Exemple :

L’arrondi à l’unité de 53,4 est  53.

Si le chiffre après la virgule est supérieur ou égal à 5 (c’est à dire appartient à {5;6;7;8;9}),

on arrondit à l’entier supérieur.

VII. Valeur approchée à l’unité

Définition :
  1. La valeur approchée à l’unité par défaut d’un nombre décimal est le nombre décimal n’ayant pas de virgule. C’est la troncature à l’unité de ce nombre.
  2. La valeur approchée à l’unité par excès d’un nombre décimal est le nombre sans virgule immédiatement supérieur à ce nombre décimal.

Exemple :

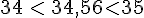34\,<\,34,56<35 , où 34 est la valeur approchée à l’unité par défaut et 35 la valeur approchée à l’unité par excès.

VIII.Valeur approchée au dixième

Il en ira de même pour « au centième », « au millième », etc.

Définition :

– La valeur approchée au dixième par défaut d’un nombre décimal est le nombre décimal ayant un seul chiffre après la virgule immédiatement inférieur à ce nombre.

C’est la troncature au dixième de ce nombre.

– La valeur approchée au dixième par excès d’un nombre décimal est le nombre décimal ayant un seul chiffre après la virgule immédiatement supérieur à ce nombre.

Exemples :

3,7<3,771<3,8 à gauche la valeur approchée au dixième par défaut, …

3,77<3,771<3,78 à droite la valeur approchée au centième par excès, à gauche… par défaut

VIII. Arrondi et valeurs approchées

Remarque :

L’arrondi à l’unité, au dixième, au centième d’un nombre décimal est celle des deux valeurs approchées par défaut ou par excès à l’unité, au dixième, au centième, qui est la plus proche de ce nombre.

Exemples :

L’arrondi au dixième de 17,527 est 17,5.

C’est la valeur approchée au dixième par défaut de 17,527.

L’arrondi au dixième de 17,493 est 17,5.

C’est la valeur approchée au dixième par excès de 17,493.

IX. Dernière comparaison entre arrondi et valeur approchée selon le signe du nombre décimal

Définition :
  1. L’arrondi de x à l’unité est une valeur approchée de x à 1 près ;si x est positif, cette valeur approchée est par défaut lorsque la première décimale de x est 0, 1, 2, 3 ou 4, par excès lorsque cette décimale est 5, 6, 7, 8 ou 9 ;
  2. si x est négatif, cette valeur approchée est par excès lorsque la première décimale de x est 0, 1, 2, 3 ou 4, par défaut lorsque cette décimale est 5, 6, 7, 8 ou 9.
  3. L’arrondi de x au dixième est une valeur approchée de x à 0,1 près ;
  4. si x est positif, cette valeur approchée est par défaut lorsque la deuxième décimale de x est 0, 1, 2, 3 ou 4, par excès lorsque cette décimale est 5, 6, 7, 8 ou 9 ;
  5. si x est négatif, cette valeur approchée est par excès lorsque la deuxième décimale de x est 0, 1, 2, 3 ou 4, par défaut lorsque cette décimale est 5, 6, 7, 8 ou 9.

Vous avez assimilé ce cours sur les rappels des notions du collège en 2de?

Effectuez ce QCM sur les rappels des notions à connaître du collège en classe de seconde.

Les nombres relatifs, les fractions et les puissances

Un QCM sur les nombres relatifs, les fractions et les puissances.


Effectuez un autre QCM sur les opérations et calculs du collège.
Nombres et calculs

Un QCM sur les nombres et calculs


Un QCM sur les rappels de certaines notions du collège.
Rappels de notions mathématiques du collège

Un QCM sur les notions d’algèbre abordées au collège.

Aidez-nous à améliorer cette page en signalant une erreur Signaler une erreur Aidez-nous à améliorer cette page en signalant une erreur
Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «rappels du collège sur les ensembles de nombres : cours de maths en 2de en PDF.» au format PDF.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

Réviser les leçons et les exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres utilitaires pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Inscription gratuite à Mathovore.  Mathovore c'est 14 099 024 cours et exercices de maths téléchargés en PDF.

✕
Mathovore

GRATUIT
VOIR