Position relative d'une droite et d'un plan : cours de maths en 2de

Sommaire de cette fiche

1 I. Les solides usuels
2 II. Droites et plans

Cours de géométrie dans l’espace en 2de sur la géométrie dans l’espace ainsi que les solides usuels (parallélépipède rectangle, pyramide, cône de révolution, cylindre de révolution, sphère et boule). Dans cette leçon en seconde, nous étudierons la position relative de droites et de plans dans l’espace.

Connaissances du collège nécessaires à ce chapitre

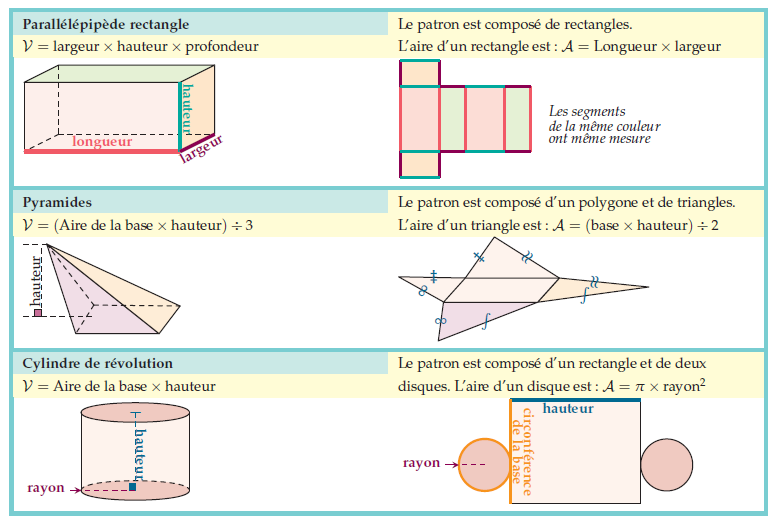
Connaître les formules d’aires des figures usuelles;
Connaître les formules de volumes des solides usuels;
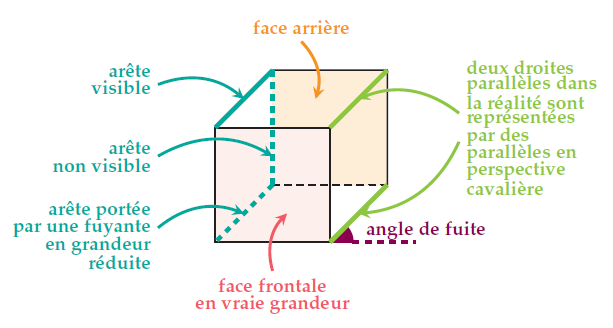
Se repérer dans une figure en perspective cavalière;
Construire un patron d’un solide usuel.

I. Les solides usuels

Définition :

Un solide est un objet en relief.
On ne peut pas le tracer en vraie grandeur sur une feuille de papier plane.

Remarques :

Un patron permet de fabriquer le solide par pliage;
La perspective cavalière permet de représenter le solide sur une feuille papier en donnant
l’impression de la 3D.

II. Droites et plans

1. Qu’est-ce qu’un plan ?

Définition :

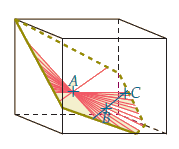
Soit A, B, C trois points de l’espace distincts et non alignés.

Pour déterminer un plan, il suffit de donner 3 points non alignés ou 2 droites sécantes ou 2 droites parallèles (non confondues).
Le plan noté (ABC) est constitué par les points des droites passant par A et parallèles ou sécantes à la droite (BC).

Remarque :

Dans chaque plan de l’espace, on peut appliquer tous les théorèmes de géométrie
plane.

Exemple :

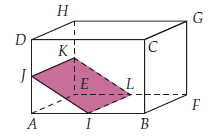
ABCDEFGH est un parallélépipède rectangle tel que :
• AB = 7 cm • I est le milieu de [AB]
• AD = 6 cm • J est le milieu de [AD]
1) Nommer le plan colorié.
2) Calculer la longueur BD.

Correction :
1) Le plan colorié coupe les arêtes du pavé en I, J, K et L, (I JK) est donc un nom possible.
2) La face ABCD du pavé est un rectangle donc le triangle ABD est rectangle en A.
D’après le théorème de Pythagore :
BD² = BA²+ AD² = 72 + 62 = 49 + 36 = 85.
Une longueur est toujours positive donc BD = $\sqrt{85}$ cm.

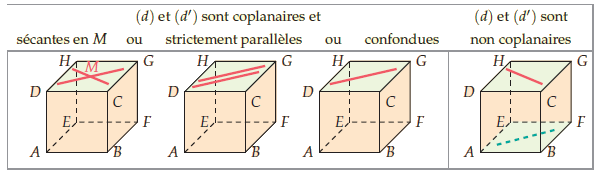
2. Positions relatives de deux droites

Définition :

Deux droites incluses dans un même plan sont dites coplanaires.

Propriété :

Deux droites de l’espace sont soit coplanaires soit non coplanaires :

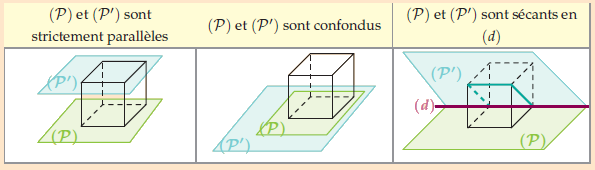
3. Positions relatives de deux plans en géométrie dans l’espace

Propriété :

Un plan coupe deux plans parallèles suivant deux droites parallèles.
Deux plans sont parallèles si et seulement si deux droites sécantes de l’un sont respectivement parallèles à deux droites sécantes de l’autre.

Remarque :

Deux plans confondus sont considérés comme parallèles.

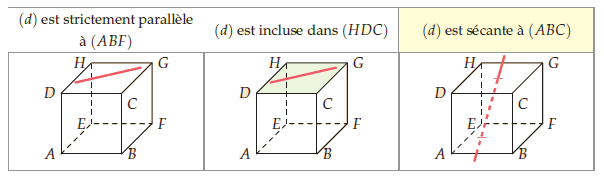
4. Positions relatives d’une droite et d’un plan

Propriété :

Une droite est parallèle à un plan si et seulement si elle est parallèle à une droite du plan.

Partagez17

Tweetez

Enregistrer

17 Partages

Télécharger et imprimer ce document en PDF gratuitement

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «position relative d'une droite et d'un plan dans l'espace : cours de maths en 2de» au format PDF.

Télécharger nos applications gratuites avec tous les cours,exercices corrigés

D'autres fiches similaires à position relative d'une droite et d'un plan dans l'espace : cours de maths en 2de.

Mathovore vous permet de réviser en ligne et de progresser en mathématiques tout au long de l'année scolaire.
De nombreuses ressources destinées aux élèves désireux de combler leurs lacunes en maths et d'envisager une progression constante. Tous les cours en primaire, au collège, au lycée mais également, en maths supérieures et spéciales ainsi qu'en licence sont disponibles sur notre sites web de mathématiques.
Des documents similaires à position relative d'une droite et d'un plan dans l'espace : cours de maths en 2de à télécharger ou à imprimer gratuitement en PDF avec tous les cours de maths du collège au lycée et post bac rédigés par des enseignants de l'éducation nationale.
Vérifiez si vous avez acquis le contenu des différentes leçons (définition, propriétés, téhorèmpe) en vous exerçant sur des milliers d'exercices de maths disponibles sur Mathovore et chacun de ces exercices dispose de son corrigé.
En complément des cours et exercices sur le thème position relative d'une droite et d'un plan dans l'espace : cours de maths en 2de, les élèves de troisième pourront réviser le brevet de maths en ligne ainsi que pour les élèves de terminale pourront s'exercer sur les sujets corrigé du baccalauréat de maths en ligne.

Position relative de deux droites dans l'espace : cours de maths en 1ère S
66
Cours de géométrie dans l'espace en classe de première avec la notion de perspective cavalière ainsi que les différentes positions relatives de deux droites dans l'espace et de plans. Cette leçon est à télécharger au format PDF. I.Perspective cavalière Dans une représentation d’un solide en perspective cavalière : une figure représentée…
Tags: plan, d, droites, parallèles, plans, l, points

Les dernières fiches mises à jour

Voici les dernières ressources mis à jour sur Mathovore (des cours, exercices, des contrôles et autres), rédigées par notre équipe d'enseignants.

Mathovore c'est 2 014 988 cours et exercices de maths téléchargés en PDF et 168 262 membres.
Rejoignez-nous : inscription gratuite.