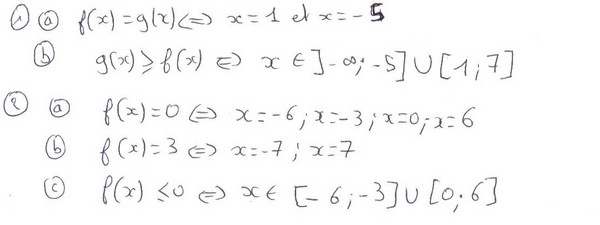Fonctions : corrigé des exercices de maths en 2de en PDF.
Mis à jour le 13 septembre 2025
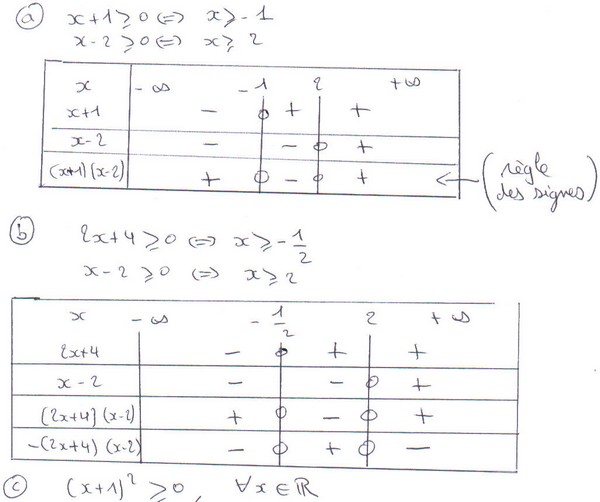
Exercice 6 :
Exercice 7 :
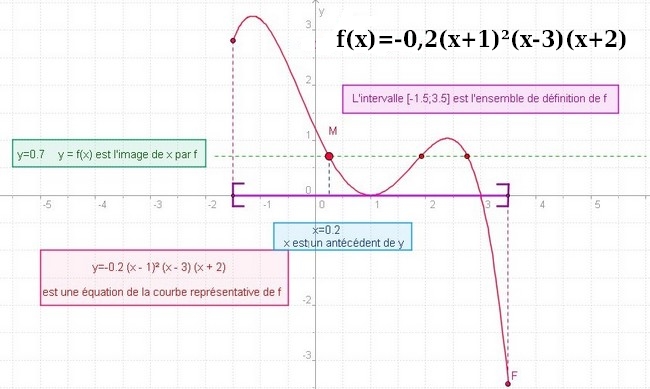
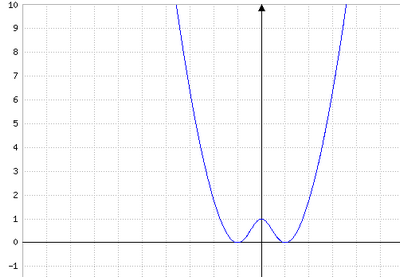
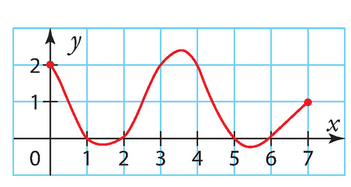
1. Déterminer par lecture graphique les images de 1et de 2.5 par la fonction f. (à 0.1 près)
f(1)=0 et f(2,5)=1
2. Retrouver les valeurs exactes de ces résultats par le calcul.
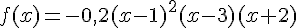

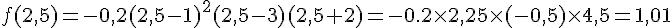
3. Déterminer graphiquement les antécédents de 1. ( toujours à 0.1 près)
Les antécédents de 1 par f sont 0,2 et 2,4
4. Résoudre graphiquement l’équation f(x) =0.
Cette équation a deux solutions qui sont x = 1 et x = 3.
5. Résoudre graphiquement l’inéquation f(x)> 1.
S= [-1,5;0,2[
Exercice 8 :
On donne
f(x) = 9x² – 4 + (3-2 x) (3x-2) et g (x) = x² +2x +1 – (2x-3)²
1. Développer, réduire et ordonner f(x) et g (x).
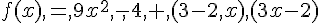
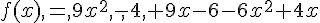
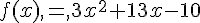
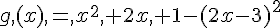
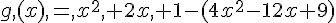
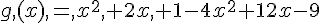
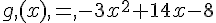
2. Factoriser f (x) et g (x).
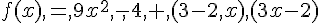
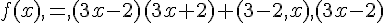
![f(x),=,(3x-2)[(3x+2)+(3-2,x)]](https://mathovore.fr/latex-images/c90f6da4af5471b44ad82376c491632f.png)
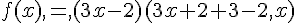
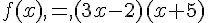
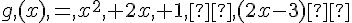
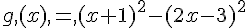
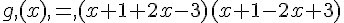
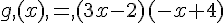
Soit la fonction rationnelle définie par h(x) = (f(x))/(g(x))
1. Déterminer la condition d’existence de h(x).
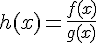
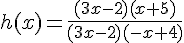
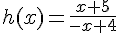
donc h existe pour 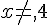
2. Simplifier h(x).
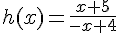
3. Résoudre les équations et inéquations suivantes :
h(x) = 0 ;
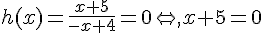
donc 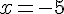
h(x) = 3
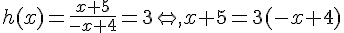
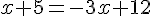

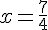
et h(x) < 0.
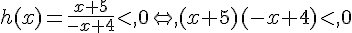
![{\color{DarkRed},S=]-\infty;-5[\cup,]4;+\infty[}](https://mathovore.fr/latex-images/a943c07114e2ca0caf13f375c88aadd2.png)
Exercice 9 :
 et
et  désignent des réels strictement positifs .
désignent des réels strictement positifs .
Un rectangle de dimension  et
et  (en centimètres) a pour aire
(en centimètres) a pour aire 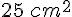 .
.
a) Exprimer  en fonction de
en fonction de  .
.
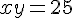
donc 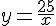 (avec
(avec 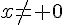 ) .
) .
b) On définit une fonction en associant à la dimension  ,
,
l’autre dimension  .
.
Quel est l’ensemble de définition de cette fonction ?
l’ensemble de déinition de cette fonction est ![]0;+\infty[](https://mathovore.fr/latex-images/b7ae82936fca7d8c8bfc1a8a7a24eb56.png) .
.
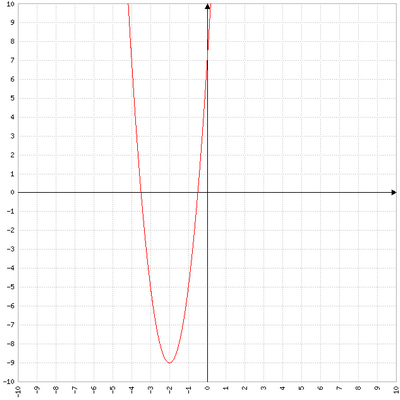
Exercice 10 :
f est la fonction définie sur  par
par 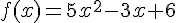 .
.
1- Démontrer que, pour tout nombre réel x, 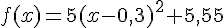 .
.
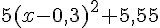

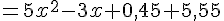
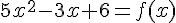
2- Résoudre graphiquement l’inéquation 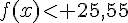 .
.
voir le graphique……
3- Factoriser 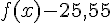 et retrouver les solutions de l’inéquation à l’aide d’un tableau de signes.
et retrouver les solutions de l’inéquation à l’aide d’un tableau de signes.
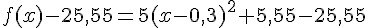
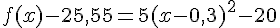
![f(x)-25,55=5[(x-0,3)^2-2^2]](https://mathovore.fr/latex-images/9fa52b0d3e11ad2f25c75e4ed41cf303.png)
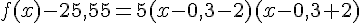
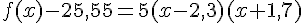
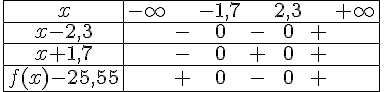
donc
![{\color{DarkRed} f(x)< 25,55\Leftrightarrow f(x)-25,55< 0\Leftrightarrow x\in]-1,7;3[}](https://mathovore.fr/latex-images/a92d2a10665f951ebee258ee8f4401fc.png) .
.
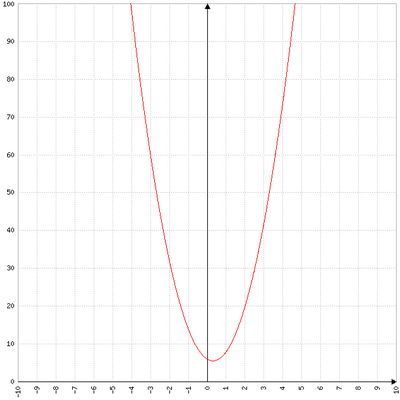
Exercice 11 :
Soit f la fonction définie sur R par f(x) = 4x² + 16x + 7
1) Démontrer que f(x) = 4(x+2)²-9
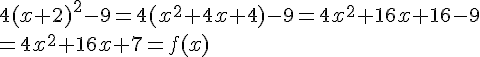
2) Factoriser f(x)

3) Choisir la forme la mieux adaptée et détailler les calcules pour calculer f(-1/2) et f(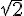 )
)
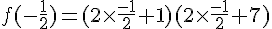
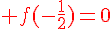
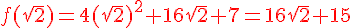
4) Dans le repère suivant tracer la représentation graphique de f
Voir la courbe ….
5 ) résoudre algébriquement f(x) = 0.
Effectuez les tracés sur la courbe …
Expliquer comment controler les solutions sur le graphique
cela revient à chercher les points d’intersection entre la courbe et l’axe des abscisses.
6a) résoudre algébriquement l’équation f(x) = 2x+7
Effectuer sur la courbe …
b) résoudre graphiquement la même équation
Effectuer sur la courbe …
7) quelle forme de f(x) permet d’affirmer que f(x) est toujours supérieur ou égal a -9.
Démontrer alors que pour tout x de R, f(x) est toujours supérieur ou égal a -9.
f(x) = 4(x+2)²-9
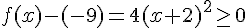
donc
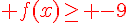
Comment controler ce résultat sur le graphique ?
la courbe a pour ordonnée minimale – 9 .
Exercice 12 :
1. On considère les fonctions f, g , h définies sur  par :
par :
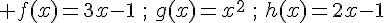 .
.
a. Donner l’expression algébrique de la fonction composée i=hofog .
Soit 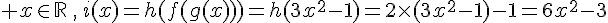
b.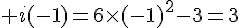
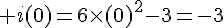 .
.
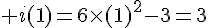 .
.
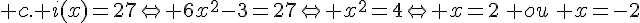
2. Décomposer les fonctions suivantes à l’aide des fonctions de référence (fonctions usuelles).
a. 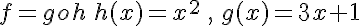 .
.
b. 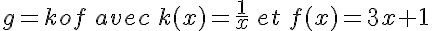 .
.
c. 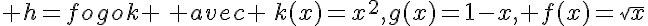 .
.
d. 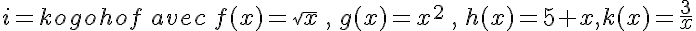 .
.
Exercice 13 :
On considère la fonction f définie sur 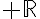 par :
par :
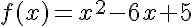 .
.
1. Montrer l’égalité des expressions algébriques suivantes :
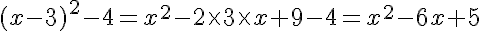
2. On considère, désormais, la fonction f définie par  :
:
a. 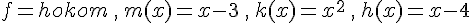
b. Sur ![]-\infty\,;\,3]](https://mathovore.fr/latex-images/d1fd3b4bcd6f815f63d5caf670bd0c1d.png) f est décroissante et sur
f est décroissante et sur 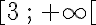 , f est croissante.
, f est croissante.
d. La valeur minimale de f est atteinte en x=3 et sa valeur est f(3)=-4.
Exercice 14 :
a. Par la fonction g, – 5 est l’image de 4.

b. 2 a pour image 0 par la fonction f.

c. Un antécédent de – 3 par h est 5.
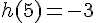
d. Les images par f de – 3 et 5 sont nulles.
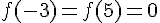
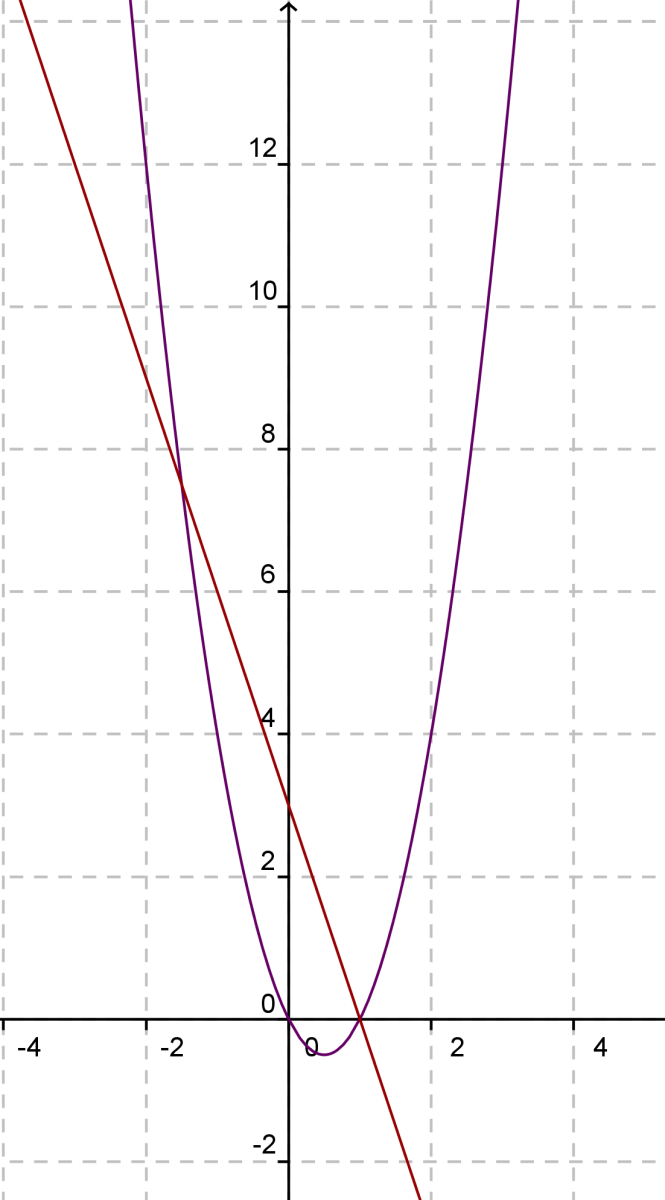
Exercice 15 :
Soient f et g deux fonctions définies sur  par :
par :
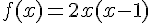 et
et 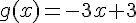 .
.
1. Tracer à l’écran de la calculatrice les courbes représentatives des fonctions
f et g.
2. Conjecturer graphiquement les solutions de l’équation 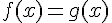 .
.
Ils y a deux points d’intersection pour 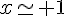 et
et 
3. Résoudre algébriquement l’équation 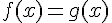 .
.
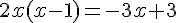
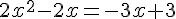
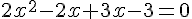
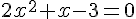
Cherchons la forme canonique.
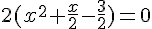
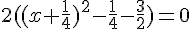
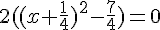
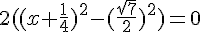
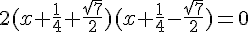
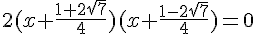

Un produit de facteur est nul si et seulement si
l’un des facteurs, au moins, est nul.
Les racines sont 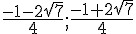 .
.
soit 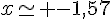 et
et 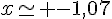
Exercice 16 :
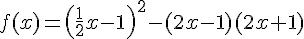
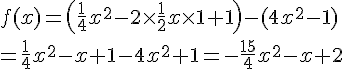
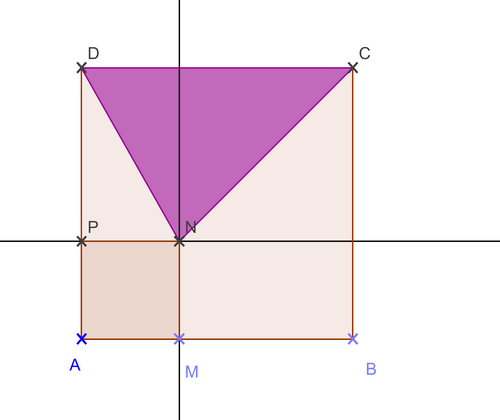
Exercice 17 :
Soit f(x) l’aire du carré AMNP et g(x) l’aire du triangle DNC
1. Exprimer f(x) en fonction de x
f(x)=x²
2. Exprimer g(x) en fonction de x
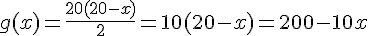
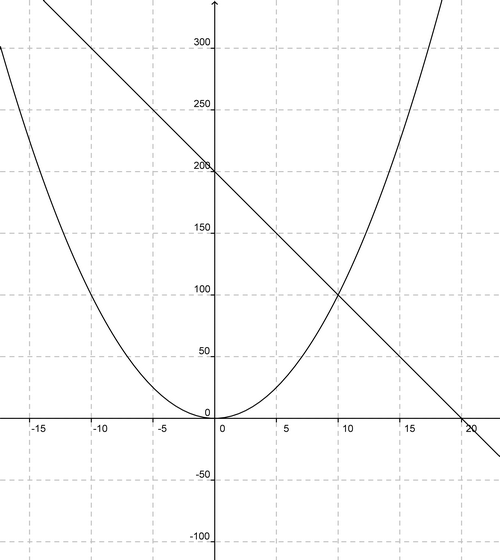
3.Représenter dans un même repère les fonctions f et g pour tout x de [0;20]
4.Déterminer graphiquement les valeurs de x pour lesquelles le carré AMNP et le triangle DNC ont la même aire .
Le nombre x étant une longueur par conséquent positif.
La seule valeur pour x est x= 10 cm .
Exercice 18 :
Partie A. Lecture graphique.
1°
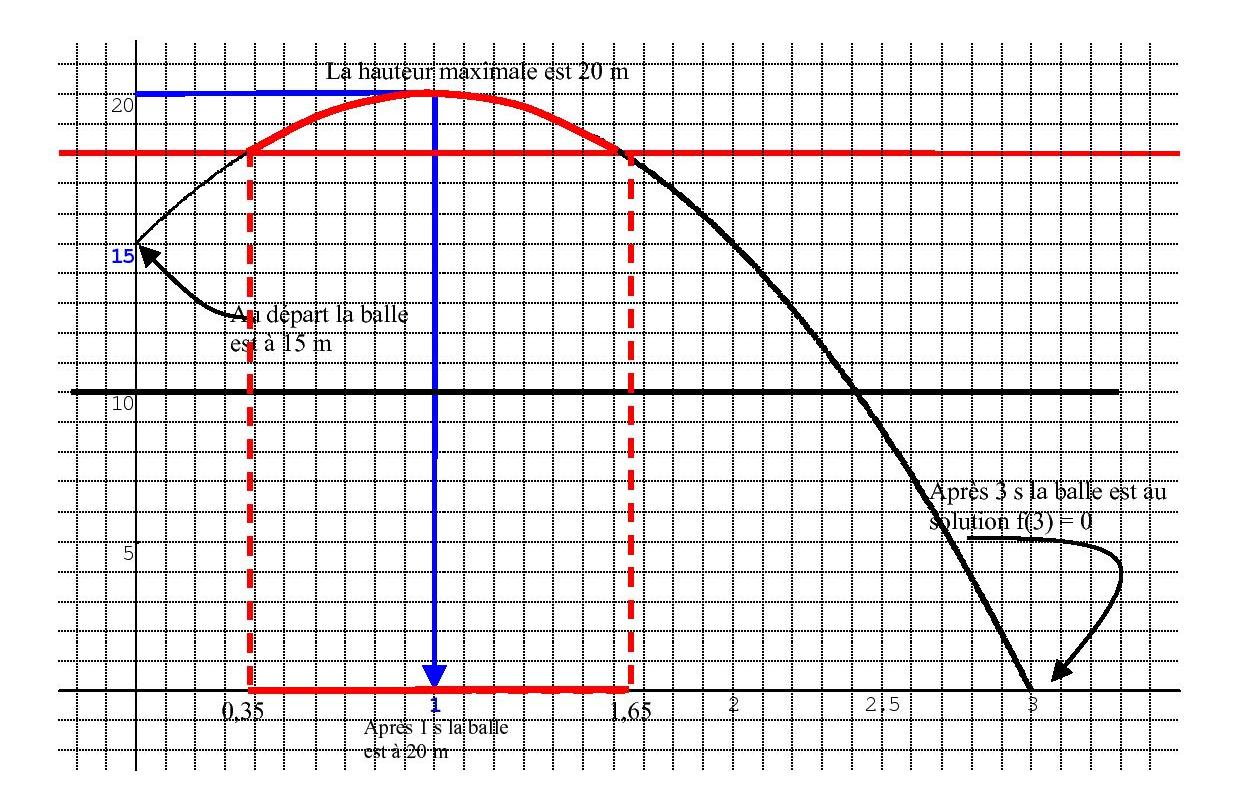
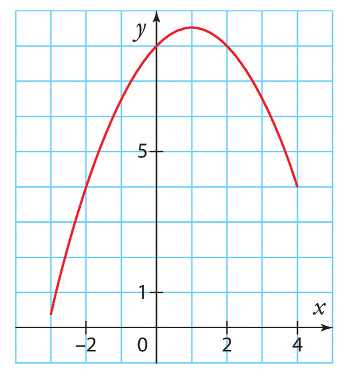
a) Pour trouver la hauteur de la balle après 10 secondes, on cherche le point correspondant sur le graphe. On lit environ f(10) = 37 m.
b) La balle a été lancée à une hauteur de f(0) = 15 m.
c) Non, la balle ne peut pas être lancée à 20 m car la hauteur maximale atteinte est d’environ 37 m, comme on l’a vu à la question a).
d) La balle revient au sol lorsque sa hauteur est égale à 0. On lit sur le graphe que cela se produit environ à x = 2,1 s.
e) f(3) ≈ 0 et f(0) = 15. f(3) représente la hauteur de la balle après 3 secondes, c’est-à-dire lorsqu’elle touche le sol, et f(0) représente la hauteur initiale de la balle, c’est-à-dire lorsqu’elle est lancée.
2°
a) La hauteur maximale est atteinte lorsque la dérivée de f(x) s’annule. On calcule d’abord la dérivée :
f'(x) = -10x + 10
On cherche le x tel que f'(x) = 0 :
-10x + 10 = 0
x = 1
La hauteur maximale est donc atteinte à x = 1. On lit sur le graphe que f(1) ≈ 40 m.
b) Pour trouver les instants où la hauteur est égale à 15 m, on cherche les points correspondants sur le graphe. On lit environ x = 0,3 s et x = 2,7 s.
c) Résoudre graphiquement f(x) ≥ 18 revient à trouver les valeurs de x pour lesquelles la courbe de f est au-dessus de la droite d’équation y = 18. On trouve que f(x) ≥ 18 pour x compris entre environ 0,45 s et 2,55 s. Cela signifie que la balle se trouve à une hauteur supérieure à 18 m pendant cette période de temps.
Partie B : Calculs .
1°
b) On a déjà trouvé f(0) = 15. Pour trouver le temps de chute, on cherche le x tel que f(x) = 0. En résolvant l’équation -5x² + 10x + 15 = 0, on trouve x = 3 s. Donc la balle revient au sol après 3 s.
2°
a) Il suffit de développer l’expression (x-1)² :
f(x) = -5x² + 10x + 15
= -5(x² – 2x + 1) + 20
= 20 – 5(x-1)²
On a bien l’expression demandée.
b) En résolvant l’équation -5(x-1)² + 20 = 15, on trouve (x-1)² = 1/5, donc x-1 = ±√(1/5), donc x ≈ 1,45 s ou x ≈ 0,55 s. On retrouve le résultat de la question 1°b), qui est f(0) = 15.
3°
Comme le coefficient de x² est négatif, la fonction f est une fonction décroissante sur l’intervalle [0 ; 3]. Donc f(0) est la hauteur maximale atteinte, et on retrouve le résultat de la question A1b).
4°
f(2) = -5(2)² + 10(2) + 15 = 5
f(2/3) = -5(2/3)² + 10(2/3) + 15 = 70/9
5°
Il s’agit de résoudre l’équation -5x² + 10x + 15 = 0. On peut la résoudre comme dans la question 1°b) en utilisant la formule quadratique, ou bien en remarquant que f(x) = 0 équivaut à f(x) = f(1) = 20 – 5(x-1)² = 0, donc à (x-1)² = 4, donc à x-1 = ±2, donc x = 3 ou x = -1. Comme x ∈ [0 ; 3], la seule solution possible est x = 3.
Exercice 19 :
Soit la fonction linéaire f : x 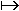
a. f(5)=6 ; f(- 1,2)=-1,44 ; f(0)=0 ; f(100)=120.
b. 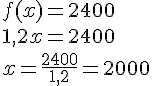
De même : 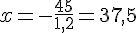
Exercice 20 :
Soit g la fonction linéaire telle que g 😡 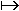
a. le coefficient de la fonction g est a = -0,4
b. g(10)=-4 ; g(-5)=2 et g(1)=-0,4.
Exercice 21 :
On sait que 18 a pour image 23 par la fonction f et que 12 a pour image 14 par f.
f est-elle une fonction linéaire ?Pourquoi ?
Calculons :
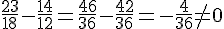
donc cette fonction n’est pas linéaire.
Exercice 22 :
Exprimer la fonction linéaire f sous la forme x 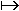
1. Lorsque l’image de 10 est – 3 alors  et
et 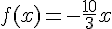
2. Lorsque f (- 100)= – 46 alors  et
et 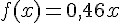 .
.
3. Lorsque le coefficient de f est 2,5 alors f(x)=2,5x .
Exercice 29 :
Partie 1 :
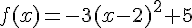
1) La fonction  est définie sur
est définie sur  .
.
2) 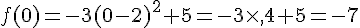

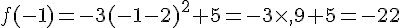
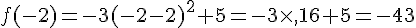
3)
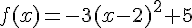


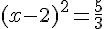
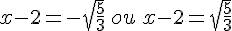
Ce sont les deux antécédents de 0.
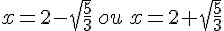
4)
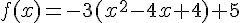

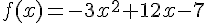
5)


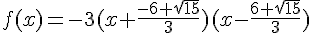
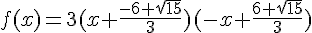
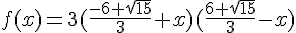
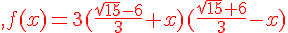
Partie 2 :
1) f(0) = 4 ; f(-2)=-2 ; f(2,5)=3 .
2) -1,3 ;0 et 2,6 sont des valeurs approchées des antécédents de 4 par f .
3) f ( -1) = 5 et f (1) = 1
4) 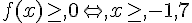
5) 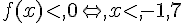
Exercice 30 :
Exercice 32 :
Exercice 33 :
1.  est définie sur
est définie sur  car le dénominateur est strictement positif .
car le dénominateur est strictement positif .
2. Le numérateur est strictement positif ainsi que le dénominateur
donc f également en tant que quotient de nombres strictement positifs .
3. f est paire ( montrer que f(-x)=f(x) ) .
4.
5. La valeur du maximum de f sur [-1 ; 1] et sur [-2;1] est 1 .
6.

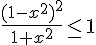
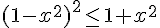 ( car
( car 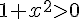 )
)
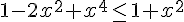
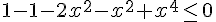
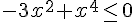
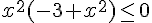
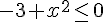

Faire un tableau de signe, et montrer que :
![S=[-\sqrt{3};\sqrt{3}]](https://mathovore.fr/latex-images/cf5524f7419c04a789917ba72c7d2c28.png)
Exercice 34 :
Soit  définie sur
définie sur  par
par 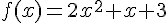
1. Calculer l’image de 0, l’image de 1 et l’image de 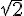 par la fonction
par la fonction  .
.
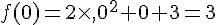
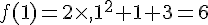
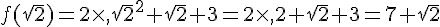
2. Déterminer le (ou les) antécédent(s) de 3 par  .
.
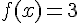
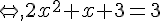
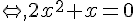
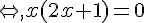
Propriété :
Un produit de facteurs est nul si et seulement si un des facteurs, au moins, est nul.
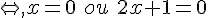
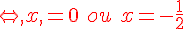
Les antécédents de 3 sont 
Exercice 35 :
 est la fonction déinifie sur
est la fonction déinifie sur  par :
par :
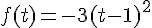 .
.
1. Calculer l’image de 2.
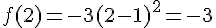
2. Calculer 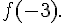
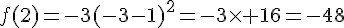
3. Est-il vrai que 4 n’admet pas d’antécédent par  ?
?
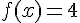
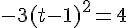
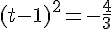
or le carré d’un nombre est positif ou nul donc en effet 4 n’admet pas d’antécédent par f.
4. Est-il vrai que 0 admet un seul antécédent par  ?
?
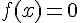
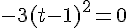
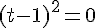
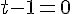
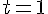
0 admet un unique antécédent par f qui est 1.
5. Déterminer un antécédent de – 12 .
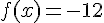
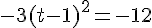



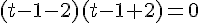
Un produit de facteurs est nul si et seulement si l’un des facteurs, au moins, est nul.
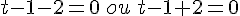
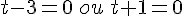
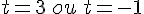
ainsi
-12 admet exactement deux antécédents par f qui sont 3 et -1.
Exercice 36 :
 est la fonction définie sur
est la fonction définie sur ![]-2;+\infty[](https://mathovore.fr/latex-images/c878284574639705d6c952cfb80fd622.png) par :
par :
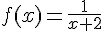
1. Expliquer pourquoi  n’est pas définie en
n’est pas définie en  .
.
car pour x=-2 le dénominateur est nul donc on ne peut pas calculer l’image de -2.
2. Calculer 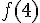 .
.
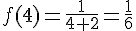
3. Déterminer l’antécédent de 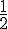 .
.
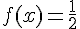
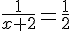
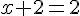
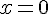
L’antécédent de 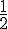 par f est 0.
par f est 0.
Exercice 37 :
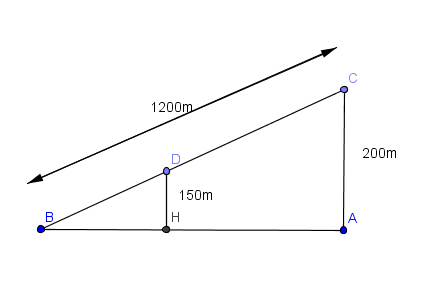
Calucule la longueur DB qu’il lui reste à parcourir.
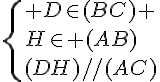 d’après la partie directe du théorème de Thalès :
d’après la partie directe du théorème de Thalès :
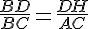
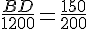
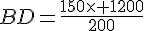
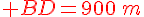
Exercice 38 :
On fabrique une boîte à partir d’une feuille de carton carrée de 18 cm de côté dont on coupe et relève les coins.
On note x la largeur de l’encoche exprimée en cm, f(x) le volume de la boîte exprimée en cm cube.
1) Donner les valeurs possibles de x.
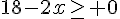
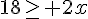
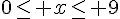
En déduire l’ensemble de définition D de f.
![D_f=[0;9]](https://mathovore.fr/latex-images/d20a7775578e08b6450f7f295638c07e.png)
2) Donner l’expression de f sur D.
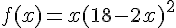
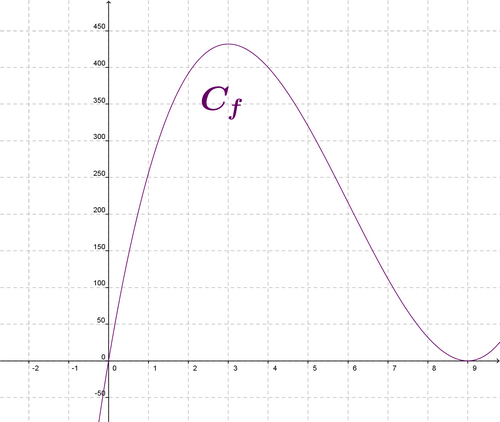
3) Représenter graphiquement cette fonction.
4) A l’aide du graphique, donner la valeur de x pour laquelle le volume de la boîte est maximal et établir le tableau de variations de la fonction f.
Le volume de la boîte est maximal pour x = 3cm .
5) Montrer que f(x) – f(3) = 4 (x – 3)² (x – 12).

et
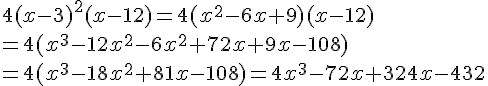
Conclusion :
f(x) – f(3) = 4 (x – 3)² (x – 12)
En déduire que f(x) est inférieur ou égal à f(3) pour tout x élément de [0;9].
Que peut-on en conclure ?
f(3) étant le maximum et f(3)=432.
Le volume maximal de la boîte est de 432 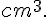
EXERCICE 39 :
1)a) On calcule 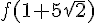 :
:
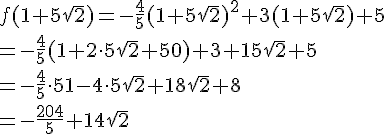
On peut donc écrire : 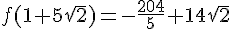
b) On calcule 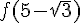 :
:
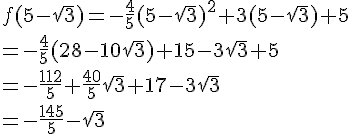
On peut donc écrire : 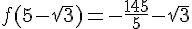
2) Pour f(x) = 1, on a :

On peut résoudre cette équation en utilisant la formule de la discriminante :
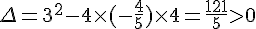
Les racines de l’équation sont alors :
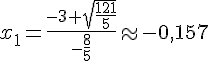
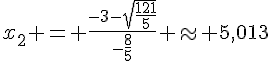
Donc il n’y a pas de réel x tel que f(x) = 1.
Pour f(2) et f(0), on calcule :
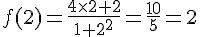
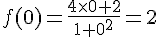
Donc les images de 2 et de 0 par f sont égales.
3) On calcule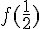 :
:
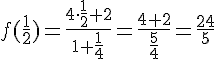
4) On résout l’équation f(x) = 0 :

On utilise la formule de la discriminante :
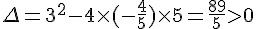
Les racines de l’équation sont alors :
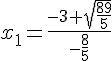

Donc les antécédents de 0 sont 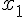 et
et 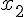 .
.
EXERCICE 40 :
1. On calcule f(3) :
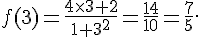
Donc f(3) n’est pas égal à 1.
2. On calcule f(2) et f(0) :
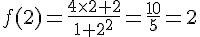
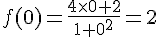
On a donc f(2) = f(0) = 2.
3. On calcule 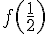 :
:
 .
.
L’image de 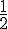 par f est donc égale à
par f est donc égale à 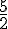 .
.
4. On cherche les antécédents de 0 par f, c’est-à-dire les valeurs de x telles que 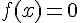 .
.
On résout l’équation 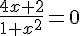 :
:
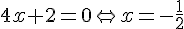 .
.
La seule solution est donc 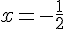 .
.
L’antécédent de 0 par f est donc 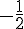 .
.
EXERCICE 41 :
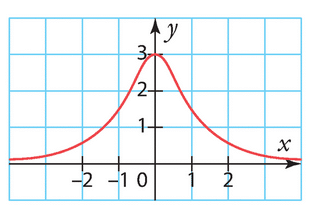
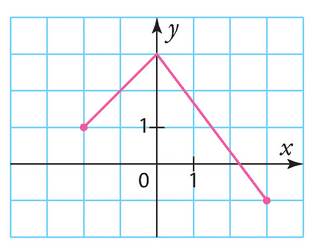
a) En lisant graphiquement, on trace une droite verticale passant par x=-1 et on cherche l’intersection avec la courbe. Cette intersection se situe à environ y=1.3. Donc l’image de -1 par f est environ 1.3.
b) En lisant graphiquement, on cherche la valeur de f(0) en lisant l’ordonnée en x=0 sur la courbe, qui est environ y=2. Donc l’image de 0 par f est environ 2.
c) En lisant graphiquement, on trace une droite horizontale passant par y=1 et on cherche les intersections avec la courbe. Il y en a deux, environ en 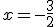 et x=2. Donc les antécédents de 1 par f sont environ
et x=2. Donc les antécédents de 1 par f sont environ 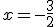 et x=2.
et x=2.
d) En lisant graphiquement, on trace une droite horizontale passant par y=3 et on cherche les intersections avec la courbe. Il y a une seule intersection, environ en x=3. Donc l’antécédent de 3 par f est environ x=3.
EXERCICE 42 :
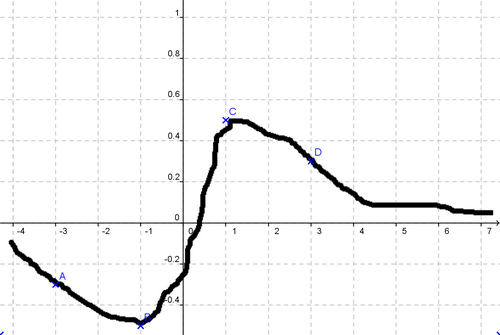
a) En lisant graphiquement, on trouve que g(0) est environ 0.5.
b) En lisant graphiquement, on cherche les valeurs de g(1) et g(-2) en lisant les ordonnées en x=1 et x=-2 sur la courbe. On trouve que g(1) est environ -1 et que g(-2) est environ -1.5.
c) En lisant graphiquement, pour trouver les antécédents éventuels de -1, on trace une droite horizontale passant par y=-1 et on cherche les intersections avec la courbe. Il y a deux intersections, environ en x=-1.5 et x=2. Donc les antécédents éventuels de -1 sont environ -1.5 et 2.
Pour trouver les antécédents éventuels de 1, on trace une droite horizontale passant par y=1 et on cherche les intersections avec la courbe. Il n’y a pas d’intersection.
Pour trouver les antécédents éventuels de 5, on trace une droite horizontale passant par y=5 et on cherche les intersections avec la courbe. Il n’y a pas d’intersection.
EXERCICE 43 :
a) En estimant sur la courbe, on peut voir que f(x)=2 a deux solutions approximativement égales à 2,5 et 6,5.
b) f(x)=0 a trois solutions approximativement égales à 1,5, 3,5 et 6.
c) f(x)=-1 a une solution approximativement égale à 5,5.
d) f(x)=1 a deux solutions approximativement égales à 1 et 5.
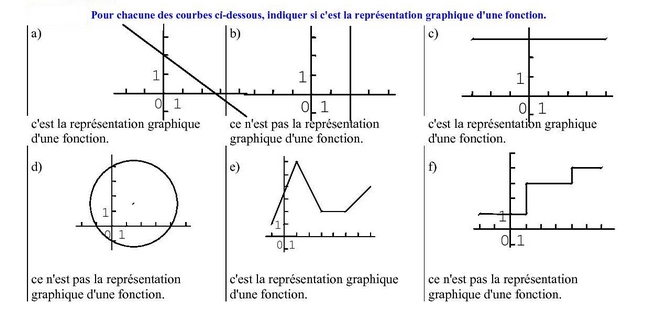
EXERCICE 44 :
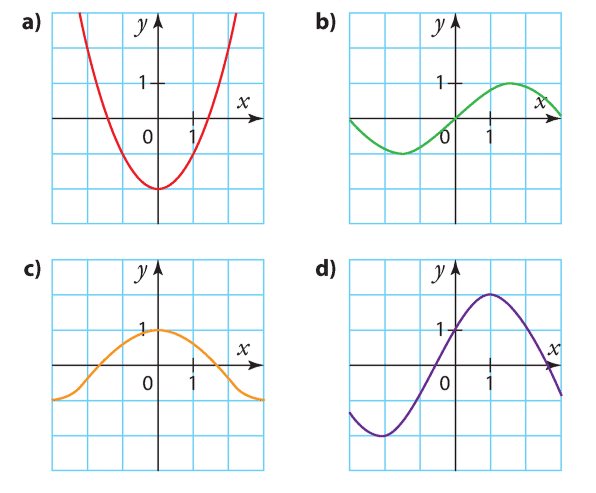
La première courbe est une fonction paire.
La deuxième courbe n’est ni paire, ni impaire.
La troisième courbe est une fonction impaire.
EXERCICE 45 :
a) La fonction est définie pour tout x sauf pour x = 10 car le dénominateur est nul.
b) g(x) >= 0 pour tout x et le domaine de définition de g est 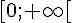 .
.
c) h(x) est définie pour tout x et son domaine de définition est 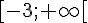 .
.
d) i(x) est définie pour tout x différent de 0 et son domaine de définition est 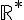 .
.
EXERCICE 46 :
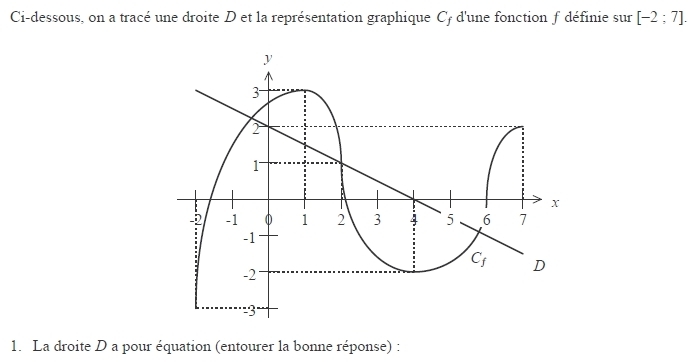
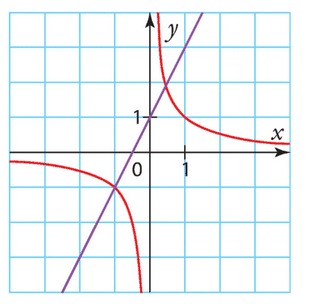
1. Les courbes associées aux fonctions sont la droite y = x/2 et la droite y=2x+1.
2. L’équation 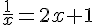 peut être réécrite sous forme
peut être réécrite sous forme 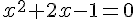 . En résolvant cette équation, on obtient les solutions
. En résolvant cette équation, on obtient les solutions 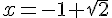 et
et 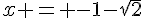 .
.
3. a) 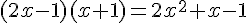 .
.
b)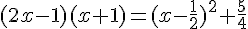 .
.
c) La parabole admet un sommet en 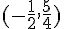 , donc la hauteur maximale atteinte par la balle est
, donc la hauteur maximale atteinte par la balle est 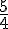 mètres.
mètres.
EXERCICE 47 :
1. La fonction n’est pas définie en 2 donc l’image de 2 ne peut pas être déterminée.
2. La fonction n’est pas définie en -2 donc la valeur de f(-2) ne peut pas être déterminée.
3. Une valeur approchée des antécédents de 5 est 0,78 et 3,22.
4. f(x) = 4 est équivalent à  . En résolvant cette équation, on obtient les solutions
. En résolvant cette équation, on obtient les solutions 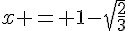 et
et 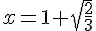 .
.
5. f(x) < 6 est équivalent à 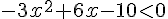 .
.
En résolvant cette inéquation, on obtient  .
.
6. 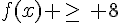 est équivalent à
est équivalent à 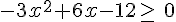 .
.
Cette inéquation est équivalente à 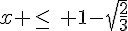 ou
ou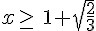 .
.
On peut aussi dire que le complémentaire de l’ensemble des antécédents de 8 est l’intervalle ![[1-\sqrt{\frac{2}{3}};1+\sqrt{\frac{2}{3}}]](https://mathovore.fr/latex-images/fbc19f62cb58c314c902d037db6993b1.png) .
.
EXERCICE 48 :
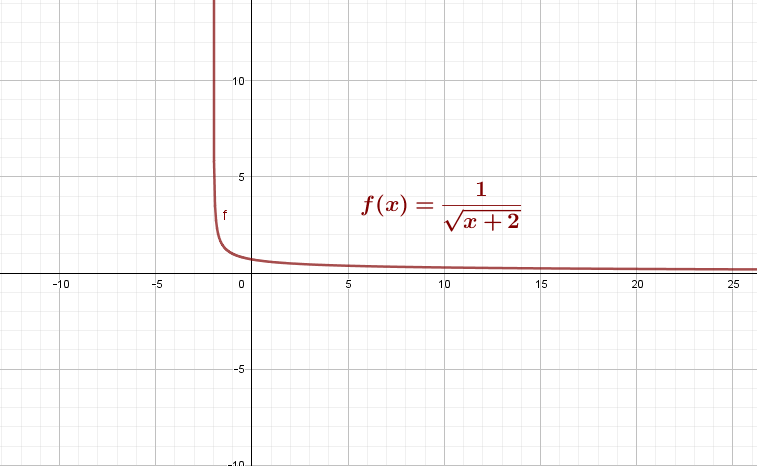
1) Df est l’ensemble des réels tels que x+2>0, soit ![D_f = ]-2, +\infty[](https://mathovore.fr/latex-images/af5366fac790cd319702b317948beefb.png) .
.
2) On calcule :
– 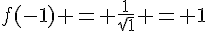 ;
;
– 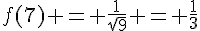 ;
;
– 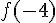 n’est pas défini car
n’est pas défini car 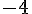 n’appartient pas à
n’appartient pas à 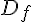 .
.
Donc, 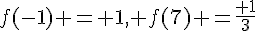 et f(-4) n’est pas défini.
et f(-4) n’est pas défini.
3) Le ou les antécédents de 2 sont les solutions de l’équation 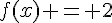 , c’est-à-dire :
, c’est-à-dire :
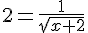 ⇔
⇔ 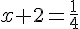 ⇔
⇔ 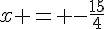 .
.
Donc, le seul antécédent de 2 est 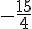 .
.
4) Le ou les antécédents de -1 sont les solutions de l’équation f(x) = -1, c’est-à-dire :
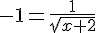 ⇔
⇔ 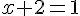 ⇔
⇔ 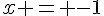 .
.
Donc, le seul antécédent de -1 est -1.
5) Voici le graphique de f :
EXERCICE 49 :
a) f(x) est définie si et seulement si 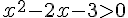 .
.
Factorisons le polynôme : 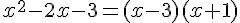 .
.
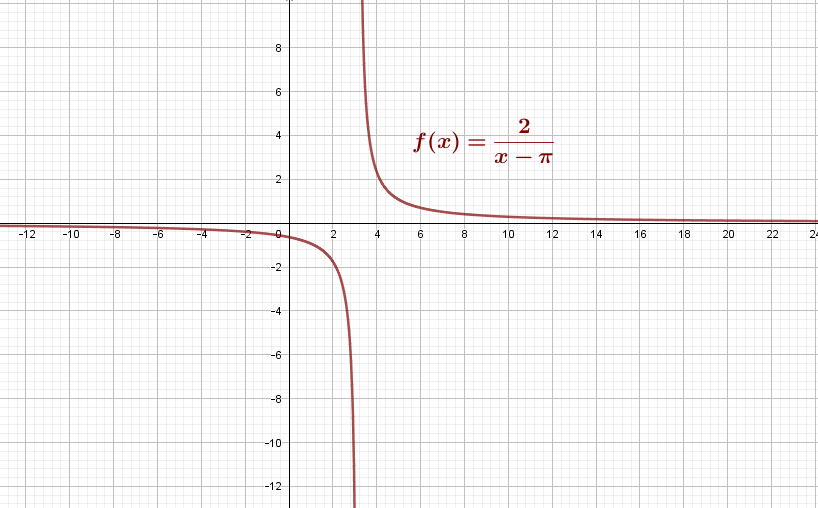
Le polynôme est négatif entre les racines, soit sur l’intervalle ]-1 ; 3[. Donc l’ensemble de définition de f est Df = ]-∞, -1[ U ]3, +∞[.
b) Pour déterminer l’image de 0, on calcule 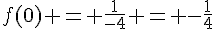 .
.
Pour déterminer l’image de 2π, on calcule 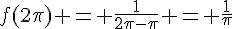 .
.
c) Pour déterminer le ou les antécédents de 2, on résout l’équation 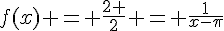 ,
,
soit 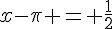 , donc
, donc 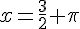 . Le seul antécédent de 2 est donc
. Le seul antécédent de 2 est donc  .
.
Pour déterminer le ou les antécédents de 0, on résout l’équation f(x) = 0 : 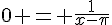 ,
,
soit x-π = ∞, donc x = ∞ + π ou x = -∞ + π.
Il n’y a pas d’antécédent de 0.
d) Pour déterminer le signe de f, on étudie le signe de l’expression x-π. Si x-π > 0, alors f(x) est négatif, si x-π < 0, alors f(x) est positif. On peut résumer cela par :
– f(x) < 0 si x > π ;
– f(x) > 0 si x < π.
e) Le graphique de f est le suivant :
La courbe est une hyperbole d’asymptotes verticales x = π et x = -1, passant par le point (0,-1/4).
EXERCICE 50 :
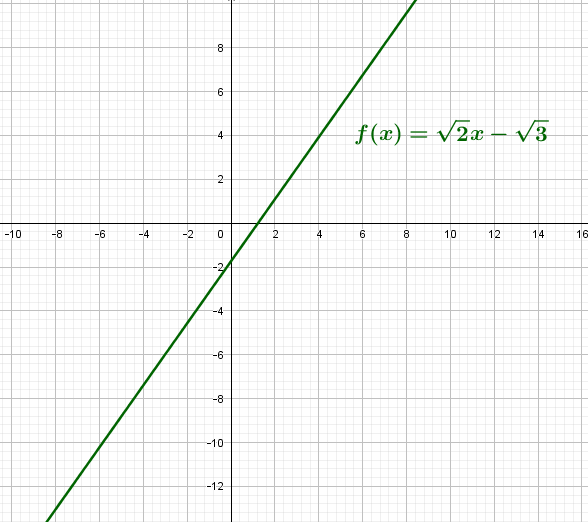
On définit la fonction f sur ℝ par 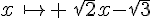
1) L’image de 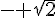 par f est
par f est 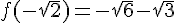 .
.
2) Pour déterminer les antécédents de 0 et 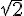 , on résout respectivement les équations
, on résout respectivement les équations 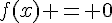 et
et 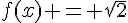 :
:
– f(x) = 0 ⇔  .
.
– 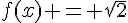 ⇔
⇔ 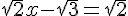 ⇔
⇔ 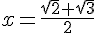 ou
ou 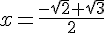 .
.
Donc, l’antécédent de 0 est √3/√2, et les antécédents de √2 sont 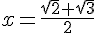 et
et 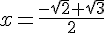 .
.
3) Pour tout réel x, on a 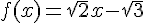 .
.
Le coefficient √2 étant positif, le signe de f(x) est le même que celui de 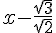 .
.
En utilisant la valeur de l’antécédent de 0, on peut en déduire que f(x) est négatif si et seulement si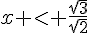 , et positif si et seulement si
, et positif si et seulement si 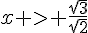 .
.
Donc, f est positive sur l’intervalle ![]\frac{\sqrt{3}}{\sqrt{2}};+\infty[](https://mathovore.fr/latex-images/fab811f4dbedd5fe73cdc8347f74e5fc.png) et négative sur l’intervalle
et négative sur l’intervalle ![]-\infty;\frac{\sqrt{3}}{\sqrt{2}}[](https://mathovore.fr/latex-images/8e60c04f7174c233a4eef0d51b40ccf3.png) .
.
4) Voici le graphique de f :
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «fonctions : corrigé des exercices de maths en 2de en PDF.» au format PDF.
Ressources de seconde
Cours de seconde
D'autres cours et exercices à consulter
🤖 Exercices IA Interactifs ✨

Des milliers d'exercices interactifs conformes aux programmes officiels. Apprenez, pratiquez et progressez à votre rythme.
Exercices interactifsL'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.