Priorités opératoires et calculs : corrigé des exercices en 5ème en PDF.

Mis à jour le 28 mai 2025

🔍Corrigés Détaillés

5eme • Scolaire

Priorités opératoires et calculs

🔎 Analyse : 16 min

🎯 Niveau : Scolaire

📱 Format : Gratuit

📄 PDF : Disponible

Le corrigé des exercices de maths en 5ème sur les priorités opératoires et les opérations. Connaître les règles de priorité des quatre opérations.

Exercice 1 :

Calcule les expressions suivantes en écrivant les étapes intermédiaires :

a) 7 + 4 x8 =7+32=39

b) 3 x11 − 7×4 =33-28=5

c) 37 − 6 x5 =37-30=7

d) 9 − 4 : 4=9-1=8

e) 32 ÷ 4 − 2 + 7×3 =8-2+21=27

f) 9 x4 : 2 − 5 x2=36:2-10=18-10=8

Exercice 2 :

Calcule les expressions suivantes en écrivant les étapes intermédiaires :

A =6 x(3 + 7) =6×10=60

B =23 − 4 x5 =23-20=3

C =(3 + 5) x(9 − 7)=8×2=16

D =(13 − 7) : 2 =6:2=3

E =5 − [4 − (2 + 1)] =5-[4-3]=5-1=4

F =(3 + 5×7) : 2 +1=(3+35):2+1=38:2+1=19+1=20

Exercice 3 :

Écrire un calcul te permettant de trouver le prix total qu’elle doit payer.

5×9+12×6,50=123 euros

Exercice 4 :

(8 + 2 )x5 =50 ; (9 − 3 )x(2 + 5 )=42 ; (8 + 4 )x(3 : 2) =18

Exercice 5 :

A=24 − 5 − 1=18

B =14 x3 − 5 x2=32

C =10 : [ 6 − 2x(1 − 0,5) ] x5=10

D =8 : 4 − 0,25×2=1,5

E =3 x(7 − 2) − 4=11

F =72 : 9 x8 : 2 − 9 x3=5

Exercice 6 :

En utilisant une seule fois les nombres 3 ; 7 ; 10 et

autant de fois que tu veux les signes + − x : ( ) essaie d’obtenir les résultats suivants :

3+7+10=20 ;10+7-3= 14 .

Exercice 7 :

Mets les parenthèses et les crochets pour que l’égalité soit vraie :

[ 5 x4 −( 1+ 2) ]x2 = 34

Exercice 8 :

Écrire l’expression permettant de calculer le montant de ses achats.

16(24+11+4,5)=632 €

Exercice 9 :

Écrire l’expression qui permet de calculer le poids du boxeur le jour du combat.

86,2-7×0,6=82 kilos

Exercice 10 :

A = 125 − 7 x4 + 11=108

B = (125 − 7) x4 + 11= 483

C = 125 − 7 x(4 + 11) = 20

D = 125 − (7 x4) + 11= 108

E = [(125 − 7) x4] + 11=483

F= 125 − [7 x(4 + 11)]=20

Exercice 11 :

1) 12,7 + 3,1×2 =18,9

2) 12,7 – 3,1×2 =6,5

3) 12,7 x3 + 3,1×7=59,8

4) 12,7 x3 − 3,1×8 = 13,3

5) (5 − 3) x(9,1 − 7,8)=2,6

6) (5 + 3) x(9,1 + 7,8)= 135,2

Exercice 12 :

A = − 4 + 15 + ( 9 – 4) – 2 + (−4 + 1 ) = 11

B = − 35 + [12 + ( 75 − 55) − (15 − 8 ) ] + 7 = – 3

C = 4 − (7 – 3 ) − [ 11 − ( 8 − 5)] = – 8

Exercice 15 :

A = 7 + 4 x8=7+32=39

B = 3 x11– 7×4=33-28=5

C = 37 – 6 x5=37-30=7

D = 9 – 4 : 4=9-1=8

E = 32 ÷ 4 – 2 + 7×3=8-2+21=27

F = 9 x 4:2 – 5 x2=36:2-10=18-10=8

Exercice 16 :

x = 132 – 11×10 + 4 x2,5=132-110+10=32

y = 12,5 – 2 – 5,1 + 15 – 1,2=19,2

z = 120 – 4×5 – 7x´8 + 54 : 9 =50

t = 22 + 3×1,5 – 1,5=25

Exercice 17 :

X = 2,9 + 0,8 x5 =6,9

T = 4 x0,5 + 3 x1,36 =6,08

C = 12,8 – 0,7 x 9=6,5

A = 10 – 9,9 : 3 =6,7

E = 0,23 x 5 + 99,18 :17,1=6,95

Exercice 18 :

M = (6 + 2) x 7=8×7=56

N = 17 x (15 – 11)=17×4=68

O = (3,5 + 6,5)x(14 – 9,5)10×4,5=45

P = (18 – 11) x(5 + 9)=7×14=98

Exercice 19 :

A =6 x (3 + 7) =6×10=60

B =23 – 4 x 5 =23-20=3

C =(3 + 5)x (9 – 7) =8×2=16

D =(13 – 7) : 2=6:2=3

E =5 – [4 – (2 + 1)] =5-(4-3)=5-1=4

F =(3 + 5x 7) : 2 +1=(3+35):2+1=38:2+1=19+1=20

Exercice 23 :
Effectuer les calculs suivants en détaillant les différentes étapes :

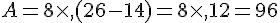
$A=8\times ,(26-14)=8\times ,12=96$

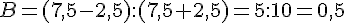
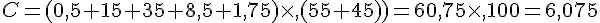
$C=(0,5+15+35+8,5+1,75)\times ,(55+45))=60,75\times ,100=6,075$
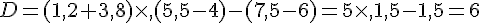
$D=(1,2+3,8)\times ,(5,5-4)-(7,5-6)=5\times ,1,5-1,5=6$

Exercice 24 :
Calculer les expressions en détaillant les calculs :

$A=7\times ,[16-(2+9)]=7\times ,(16-11)=7\times ,5=35$
$B=[9-(9-8)]\times ,[(2+7):3]=8\times ,3=24$
$C=4\times ,[39,2-(2,4+4,8)+3]=4\times ,35=140$
$D=120:,[(66-(25+8-7)):2+3]=120:(40:2+3)=120:23=\frac{120}{23}$ .

Exercice 25 :
a. La somme de 7,5 et du produit de 3 par 1,5 ;

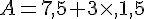
$A=7,5+3\times ,1,5$

b. Le produit de 7,5 par la somme de 3 et 1,5 ;

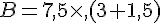
$B=7,5\times ,(3+1,5)$

c. Le quotient de la somme de 12 et 8 par 100 ;

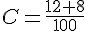
$C=\frac{12+8}{100}$

d. La somme du produit de 3 par 6 et du résultat de la soustraction de 7 à 15.

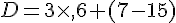
$D=3\times ,6+(7-15)$

Exercice 26 :

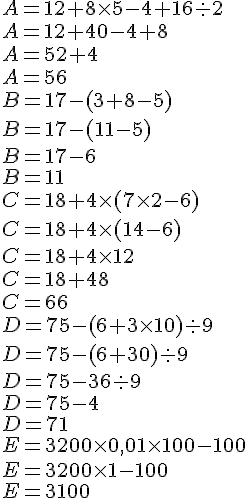
$A = 12 + 8 \times 5 - 4 + 16 : 2 \\A=12+40-4+8\\A=52+4\\A=56\\ \. \\B = 17 -(3 + 8 - 5)\\B = 17 -(11 - 5)\\B = 17 -6\\B=11 \\C = 18 + 4 \times (7 \times 2 - 6)\\C = 18 + 4 \times (14 - 6)\\C = 18 + 4 \times 12\\C = 18 + 48\\C=66 \\D = 75 - (6 + 3 \times 10) : 9\\D = 75 - (6 + 30) : 9 \\D = 75 - 36 : 9\\D = 75 - 4\\D=71 \\E = 3 200 \times 0,01 \times 100 - 100 \\E = 3 200 \times 1-100\\E=3100$

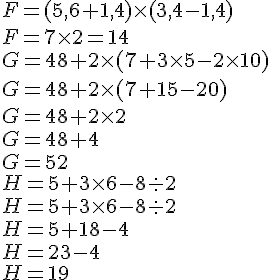
$\\F = (5,6 + 1,4) \times (3,4 - 1,4)\\F = 7 \times 2=14\\ \\G = 48 + 2 \times (7 + 3 \times 5 - 2 \times 10) \\G = 48 + 2 \times (7 + 15 - 20) \\G = 48 + 2 \times 2\\G = 48 + 4\\G = 52\\H = 5 + 3 \times 6 - 8 : 2 \\H = 5 + 3 \times 6 - 8 : 2\\\\H = 5 + 18 - 4\\H = 23 - 4\\H =19$

Exercice 27 :

A = 12 + (3 × [5 + (4 × 7) + 2]) + (8 × 3)

A = 141

B = 25 – [12 – (3 + 4)]

B = 20

C = 81 + [(7 + 21) – 13] – (17 – 9)

C = 88

D = [(7,8 – 4,5) + 11]×(4 + 3)

D = 100,1

E = 6 + [(7 × 2) – (1,1 × 2)]

E = 17,8

Exercice 28 :

Combien d’étagères remplira-t-il ?

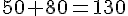
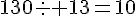
Il les rangera dans 10 étagères.

Exercice 29 :

Lors d’une brocante, Marc a acheté 8 livres, 4 dvd et 2 bd.

Chaque livre coutait 1.5 euro et une bd 4 euros.

Il a paye en tout 38 euros .

Quel est le prix d’un DVD ?

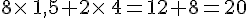
$8\times \,1,5+2\times \,4=12+8=20$

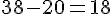
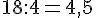
Conclusion : Le prix d’un dvd était de 4,5 euros .

Exercice 30 :

Calculer les expressions suivantes en écrivant les étapes intermédiaires :

a) 7 + 4x 8=7+32=39

b) 3×11 − 7x 4 =33-28=5

c) 37 − 6x 5 = 37-30 =7

d) 9 − 4 : 4 = 9-1=8

e) 32 ÷ 4 − 2 + 7 x 3 =8-2+21=6+21=27

f) 9 x4 : 2 − 5x 2=36:2-10=18-10=8

Exercice 31 :
1) Un éleveur possède 102 œufs et en ramasse 18 autres. Il doit expédier ses œufs par boîte de 12. Combien expédiera-t-il de boîtes ?

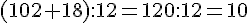
2) L’intendance du collège achète 102 cartons de papier blanc et 12 de papier de couleur. Un carton coûte 18 €.
Quel est le prix total à payer ?

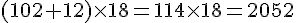
$(102+12)\times 18=114\times 18=2052$

3) Un grand magasin reçoit sa livraison de jus de fruit, soit 18 cartons de 12 bouteilles. Il reste en réserve 102
bouteilles. Combien y a-t-il maintenant de bouteilles de jus de fruit dans ce grand magasin ?

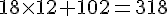
$18\times 12+102=318$

Exercice 32 :

Un libraire a reçu un premier colis contenant 50 tomes d’Harry Potter,
puis un second en contenant 80.
Il les range sur des étagères qui peuvent contenir 13 livres.
Combien d’étagères remplira-til ?

Il a reçu au total 130 livres (80+50 = 130 ).

130:13=10

Il remplira 10 étagères .

Exercice 33 :

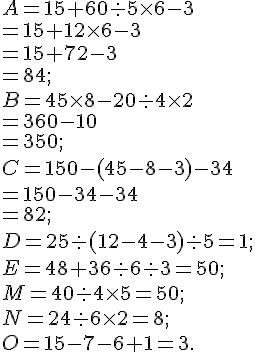
$A = 15 + 60 : 5 \times 6 - 3 \\= 15 +12\times 6 - 3\\= 15 +72 - 3\\= 84; \\ B = 45 \times 8 - 20 : 4 \times 2\\= 360 - 10\\=350 ; \\ C = 150 - (45 - 8 - 3)- 34\\= 150 - 34- 34\\=82 ;\\ D = 25 : (12 -4 -3) : 5 =1;\\ E = 48 + 36 : 6 : 3=50 ;\\ M = 40 : 4 \times 5=50 ; \\ N = 24 : 6 \times 2=8 ;\\ O = 15 - 7 - 6 + 1=3.$

Exercice 34 :
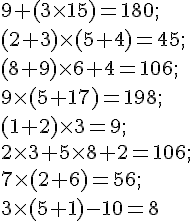
$9 +( 3\times 15) = 180 ;\\ (2 + 3) \times ( 5 + 4 )= 45 ;\\ (8 + 9)\times 6 + 4 = 106 ; \\ 9 \times (5 + 17) = 198 ;\\( 1 + 2 )\times 3 = 9 ; \\ 2 \times 3 + 5 \times 8 + 2 = 106 ;\\ 7 \times (2 + 6) = 56 ; \\ 3\times (5 + 1) - 10 = 8$

Exercice 35 :

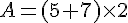
$A =(5 + 7)\times 2$

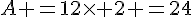$A =12\times 2 =24$ ;

B= 5 + 7x 2=5+14=19 ;

C= (12 – 4)x 3=8×3=24 ;

D= 12 – 4 x 3=12-12=0 ;

E= (21 – 18)x (12 – 10) + 1

E=3×2+1=7.

F= 18 + [12 – 2x (13 – 9)]

F=18+(12-2×4)

F=18+12-8

F=22.

G= (4,8 – (2,5 + 0,3))x (3 + 3,5)

G=(4,8-2,8)x6,5

G=2×6,5

G=13

H =[18 + 2 x(120 – 45)] x1,5

H=(18+2×75)x1,5

H=168×1,5

H=252

I =700 – [300 – (300 – 80)].

I = 700- (300-500)

I = 700- ( -200)

I = 700+200=900

Exercice 36 :

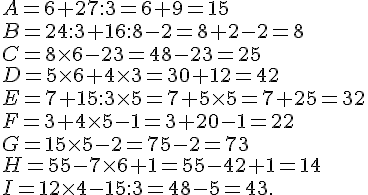
$A= 6 + 27 : 3=6+9=15 \\ B = 24 : 3 + 16 : 8 - 2 =8+2-2=8\\ C = 8\times 6 -23=48-23=25 \\ D = 5\times 6 + 4 \times 3=30+12=42\\ E = 7 + 15 : 3 \times 5=7+5\times 5=7+25= 32\\ F = 3 + 4 \times 5 - 1 =3+20-1=22\\ G = 15\times 5 - 2=75-2=73 \\ H = 55 - 7 \times 6 + 1=55-42+1=14\\ I = 12 \times 4 - 15 :3=48-5=43.$

Exercice 37 :

Écris en une seule expression le calcul donnant la monnaie rendue, puis effectue le calcul.

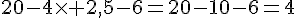
$20-4\times 2,5-6=20-10-6=4$

On lui a rendu 4 euros .

Exercice 38 :

J’ai acheté un bidon d’huile à 12 € et quatre pneus à 45 € l’un.

Écris en une seule expression le calcul donnant le montant de la dépense.

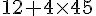
$12+4\times 45$

Effectue ensuite ce calcul.

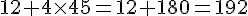
$12+4\times 45=12+180=192$

Le montant de la dépense est de 192 euros .

Exercice 39 :

· F est le produit de 4 par la somme de 12 et de 5.

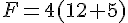
· G est la somme du produit de 6 par 8 et de 20.

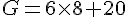
$G=6\times 8+20$

· H est la somme de 9 et du produit de 11 par 3.

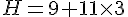
$H=9+11\times 3$

· I est le quotient de la somme de 8 et 4 par 6.

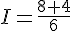
$I=\frac{8+4}{6}$

· J est la différence de 7 et du quotient de 25 par 7.

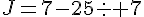
· K est le quotient de 9 par la différence de 7 et 4.

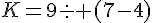
· L est le produit de la différence de 15 et 7 par 8.

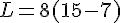
· M est la somme du produit de 8 par 4 et du produit de 7 par 3.

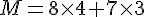
$M=8\times 4+7\times 3$

· N est le produit de la somme de 15 et 7 par la différence de 17 et 5.

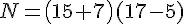
Exercice 40 :

Calculer les expressions suivantes en écrivant les étapes intermédiaires :

a) 7 + 4 $\times$ 8=39 b) 3 $\times$ 11 − 7 $\times$ 4 =5 c) 37 − 6 $\times$ 5=7

d) 9 − 4 : 4 =8 e) 32 ÷ 4 − 2 + 7 $\times$ 3 =27 f) 9 $\times$ 4 : 2 − 5 $\times$ 2=8

Exercice 41 :

Calculer les expressions suivantes en écrivant les étapes intermédiaires :

A = 6 $\times$ (3 + 7)=60 B = 23 − 4 $\times$ 5 =20 C = (3 + 5) $\times$ (9 − 7) =16

D = (13 − 7) : 2=3 E = 5 − [4 − (2 + 1)] =4 F = (3 + 5 $\times$ 7) : 2 +1=20

Exercice 43 :

Aurélie achète 5 pots de confitures à 1,50 € pièce et 12 baguettes à 0,95 € pièce.

Écrire un calcul te permettant de trouver le prix total qu’elle doit payer.

5×1,5+12×0,95=18,90 €

Aurélie devra payer 18,90 €.

Exercice 44 :

Recopier sur ta feuille les expressions suivantes en ajoutant des parenthèses pour que l’égalité soit vraie :

(8 + 2) $\times$ 5 = 50 ; (9 − 3) $\times$ (2 + 5) = 42 ; ( 8 + 4) $\times$ 3 : 2 = 18

Exercice 45

Calculer les expressions suivantes :

A = 24 − 5 − 1=18 B =14 $\times$ 3 − 5 $\times$ 2 =32 C = 10 : [ 6 − 2 $\times$ (1 − 0,5) ] $\times$ 5=10

D = 8 : 4 − 0,25 $\times$ 2 =1,5 E = 3 $\times$ (7 − 2) − 4 =11 F = 72 : 9 $\times$ 8 : 2 − 9 $\times$ 3=5

Exercice 46 :

En utilisant autant de fois les nombres 3 ; 7 ; 10 et autant de fois que tu veux les signes + − $\times$ : ( ) essaie d’obtenir les résultats suivants :

20=7+3+10 ; 14=10+(7-3) ; 31=3×10+10:(3+7) ; 67=3x(10+10)+7 ; 40=10x(7-3) ; 1=3:3.

Exercice 47 :

Mets les parenthèses et les crochets pour que l’égalité soit vraie :

[5 $\times$ ( 4 − 1) + 2] $\times$ 2 = 34

Exercice 48 :

L’entraîneur d’une équipe de football doit acheter 16 équipements pour ses joueurs.

Chaque équipement est composé d’un maillot à 24€, d’un short à 11€ et d’une paire de chaussettes à 4,50€.

Écrire l’expression permettant de calculer le montant de ses achats.

16x(24+11+4,5)=632 €

Exercice 49 :

Un boxeur pèse 86,2 kg à une semaine d’un combat.

Il fait un régime qui lui permet de perdre 0,6 kg pendant 7 jours.

Écrire l’expression qui permet de calculer le poids du boxeur le jour du combat.

86,2-7×06=82 kg

Exercice 50 :

Calculer les expressions suivantes:

A = 125 − 7 $\times$ 4 + 11=108

B = (125 − 7) $\times$ 4 + 11=483

C = 125 − 7 $\times$ (4 + 11)=20

D = 125 − (7 $\times$ 4) + 11=108

E = [(125 − 7) $\times$ 4] + 11=483

F = 125 − [7 $\times$ (4 + 11)]=20

Exercice 51 :

Calculer en respectant les priorités:

1) 12,7 + 3,1 $\times$ 2 =18,9 2) 12,7 – 3,1 $\times$ 2 =6,5 3) 12,7 $\times$ 3 + 3,1 $\times$ 7=59,8

4) 12,7 $\times$ 3 − 3,1 $\times$ 8=13,3 5) (5 − 3) $\times$ (9,1 − 7,8) =2,6 6) (5 + 3) $\times$ (9,1 + 7,8)=135,2

Exercice 52 :

En écrivant les étapes intermédiaires, calculer les expressions suivantes :

A = = − 4 + 15 + ( 9 – 4) – 2 + (−4 + 1 )=11

B = − 35 + [12 + ( 75 − 55) − (15 − 8 ) ] + 7=-3

C = 4 − (7 – 3 ) − [ 11 − ( 8 − 5)]=-8

Exercice 53 :

Pour chaque égalité, indiquer si elle est exacte ou corriger en plaçant les parenthèses indispensables.

a) 6 + 5 $\times$ 5 – 3 = 28 b) (6 + 5) $\times$ 5 – 3 = 52

c) 6 + 5 $\times$ ( 5 – 3 )= 16 d) (6 + 5 ) $\times$ (5 – 3) = 22

Exercice 54 :

Calculer en indiquant les étapes intermédiaires :

A = 25 − 7 $\times$ (8 − 5)=4 B = (7 − 4) $\times$ 3 + 4 − (7 $\times$ 2 − 8)=7

C = 8 $\times$ 3 − (12 : 3 + 2) $\times$ 3 =6 D = [10 + 5 $\times$ (6 – 4)] : 4=5

Exercice 55 :

Relier par une flèche chaque calcul à son résultat :

(5 + 5) $\times$ (5 + 5) =100

5 $\times$ (5 + 5 + 5) ) =75

5 + ((5 + 5) $\times$ 5) =55

(5 + 5) $\times$ (5 : 5) =10

(5 + (5 $\times$ 5)) : 5 =6

Exercice 56 :

Au rayon lait d’un supermarché, il y a au début de la journée 52 packs de 6 bouteilles de lait chacun.

Dans la journée, il s’est vendu 18 packs entiers et 63 bouteilles à l’unité.

1) Écrire une expression avec parenthèses permettant de calculer le nombre de bouteilles restant dans le rayon à la fin de la journée.

52×6-18×6+63=267

2) Écrire aussi une expression sans parenthèse.

(52-18)x6 +63=267

Exercice 57 :

On donne l’expression littérale E = 2x + y (3y − x ) − 5

1) Calculer E lorsque x = 2 et y = 3

E=2×2+3x(3×3-2)-5=20

2) Calculer E lorsque x = 3,5 et y = 1

E=2×3,5+1x(3×1-3,5)-5=1,5

3) Calculer E lorsque x = 3 et y = 2

E=2×3+2x(3×2-3)-5=7

Exercice 58 :

Effectuer les calculs suivant en soulignant le calcul en cours.

A=24+3×7 =45 B=720 : 9+4=84

C=60-14+5×3+2=63 D=8×3-5×4×0,2=20

E=15 :5-2=1

Exercice 59 :

Effectuer les calculs suivant en soulignant le calcul en cours.

A=25-(8-3)+1=21 B=25-(8-3+1)=19

C=18-[4×(5-3)+2] =10 D=[2+0,1×(5+3)] :4=0,7 E=24 :[8-(3+1)]=6

Exercice 60 :

Placer les parenthèses pour que les égalités suivantes soient vraies et vérifier chacune de vos réponses.

a) 4×(2+9)=44 b) 1+13-(14-7)=7 c) (15-3)×2=24

d) 2×(5-2)×(4+1)=30 e) 32 – [(4+7)×2]=10 f) 7+(7+6)×7=98

Exercice 61 :

Associer chaque expression à une phrase :

7×(4+3) > Le produit de 7 par la somme de 4 et de 3

7×4+3 > La somme du produit de 7 par 4 et de 3

4×3-7 > La différence du produit de 4 par 3 et de 7

(7-4) ×3 > Le produit de la différence de 7 et 4 par 3

Exercice 62 :

Traduis chaque phrase par une expression mathématique .

a) A est la somme du produit de 5 par 2 et de 3 alors A=5+2×3

b) B est le produit de 4 par la somme de 9 et de 7 alors B=4x(9+7)

c) C est la différence de 17 et du produit de 4 par 3 alors C=17-4×3

d) D est le quotient de la somme de 19 et 3 par 11 alors D=(19+3):11

Exercice 63 :

Calculer les expressions suivantes sur votre cahier.

A=35-[4× (5+2)-7]=14

B=12×[32-(4+7) ×2]=120

C=(1+7) ×[11-(2+3)]=48

D=12+[(120-20)-2×4×5]=72

E=150-10-[(12+2) ×4+2]=82

F=(60-59,9) ×[30-(25-15)]=2

Exercice 64 :

I) Calculer :

A = 12 + 8 × 5 − 4 + 16 : 2=56

B = 17 – (3 + 8 – 5)=11

C = 18 + 4 × (7 × 2 – 6)=50

D = 75 – (6 + 3 × 10) : 9=71

E = 3 200 × 0,01 × 100 − 100=3 100

F = (5,6 + 1,4) × (3,4 − 1,4)=14

G = 48 + 2 × (7 + 3 × 5 − 2 × 10)=52

H = 5 + 3 × 6 – 8 : 2=19

I = 24,1 − [9 − (2 + 5)]=17,1

J = 15,1 − [17 − (30 − 20)]=8,1

K = 128 − 4 × (6 + 1) + 218 − 3 × (7 – 1)=300

L = 8 + 2 × (15 − 5 × 2 + 4)=26

M = 8 × [9 − (2 + 4)] − 5 + 2=21

N = 6 + 4 × [2 × (11 − 4 × 2 + 2) − (9 − 5)]=30

O = 17 − [3 × (5 − 2) + 8] + 12,3 × 4 − 4=45,2

P = 3,5 × [12 − (7 + 3)]=7

Q = 2,5 × [3 + 2 × (13 − 3 × 3) − 6 − 3]=5

R = 38 − 8 × (7 − 2 × 3 + 1) − 4 + 2=20

S = 6 + 2 × 8 – 5 × 3 + 10 : 2=12

T = [(6 + 2) × (8 – 5) × 3 + 10] : 2=41

U = 6 + [2 × (8 – 5) × 3 + 10 : 2]=29

V = (19 – 7) × 4 – (28 – 14)=34

W = 25 – [18,7 – (9,2 + 4,5)]=20

X = [35 – (17 – 6)] : 8=3

Y = 2 × [(25 – 17,1) × 3 + 11,3]=70

Z = [35 – 56 : (28 – 20)] × 10=280

II) Calculer astucieusement :

A = 123,45 + 89,12 + 546,55 + 15,15 + 40,88=815,15

B = 8 × 8765,43 × 4 × 0,125 × 2,5=87 654,3

C = 45,13 + 136,38 + 124,87 + 56,48 + 72,62=435,48

D = 0,4 × 56,49 × 12,5 × 25 × 0,08=564,9

E = 56,98 + 76,59 + 34,18 + 14,02 + 12,41=194,18

F = 17,3 + 12 × 2 + 1,4 + 2,7 + 2,3 × 2=50

G = 2 – 1,2 + 0,71 + 1,1 × 2 + 12 + 0,29=16

H = 0,123 + 0,1 + (0,577 + 0,2)=1

4.4/5 - (23667 votes)

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «priorités opératoires et calculs : corrigé des exercices en 5ème en PDF.» au format PDF.

Ressources de cinquième

Cours de cinquième

Nombres relatifs : cours de maths en 5ème

Nombres relatifs et repérage

Droites remarquables du triangle

Les triangles et son cercle circonscrit et l’inégalité triangulaire

Proportionnalité

Fractions

Les angles correspondants et alternes-internes

Exercices de cinquième

×12

L'équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs

200+ Années cumulées

Quotidien Mise à jour

Nos applications

Téléchargez gratuitement la dernière version de nos applications.

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.

Priorités opératoires et calculs : corrigé des exercices en 5ème en PDF.

Ressources de cinquième

Cours de cinquième

Exercices de cinquième

L'équipe Mathovore

12 Enseignants Titulaires

Nos ressources pédagogiques