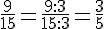Fractions : cours de maths en 5ème en PDF.

Mis à jour le 29 juin 2025

Accueil >> Collège >> Maths 5ème >> Cours de maths >> Cours en 5ème >> Fractions : cours de maths en 5ème en PDF.
🧮Cours de Mathématiques
5ème • Collège
Fractions
📖 Temps de lecture : 5 min
🎯 Niveau : Collège
📱 Format : Gratuit
📄 PDF : Disponible
Les fractions dans un cours de maths en 5ème ou nous verrons la définition du quotient et la comparaison de deux fractions ainsi que le placement sur une droite graduée. Nous terminerons cette leçon en cinquième avec du calcul numérique sur l’addition, la soustraction et la multiplication.

1. Règle de simplification de fractions :

Propriété :

On ne modifie pas la valeur d’un quotient si on multiplie (ou divise) le numérateur et le dénominateur par un même nombre non nul.

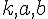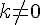On considère trois nombres relatifs k,a,b  avec k\neq0.

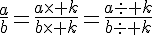
\frac{a}{b}=\frac{a\times k}{b\times k}=\frac{a: k}{b: k}

a) Simplification d’une fraction :

Méthode :
On trouve un diviseur en commun du numérateur et du dénominateur.

Exemple :   \frac{9}{15}=\frac{9:3}{15:3}=\frac{3}{5}

On ne peut pas simplifier davantage cette fraction, on dit que la fraction 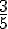\frac{3}{5} est irréductible.
Exercice  :
Simplifier les fractions suivantes 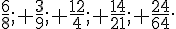\frac{6}{8}; \frac{3}{9}; \frac{12}{4}; \frac{14}{21}; \frac{24}{64}.

b) Réduction de fractions au même dénominateur :

Méthode :
On détermine un multiple commun (le plus petit possible) aux dénominateurs des fractions puis on procède comme dans l’exemple ci-dessous.

Exemple :

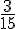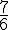Réduire les fractions \frac{3}{15} et \frac{7}{6} au même dénominateur.

Le plus petit multiple commun à 15 et 6 est 30 donc le dénominateur commun à ces deux fractions est 30 et on a alors :

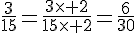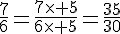
\frac{3}{15}=\frac{3\times 2}{15\times 2}=\frac{6}{30}  et  \frac{7}{6}=\frac{7\times 5}{6\times 5}=\frac{35}{30}

Remarque :
Cela permet, entre autres,  de comparer deux ou plusieurs fractions.

2) Addition et soustraction de deux ou de plusieurs fractions :

Méthode :

On réduit les fractions au même dénominateur (si ce n’est pas déjà le cas) puis on ajoute ou on soustrait les numérateurs obtenus et enfin, on simplifie la fraction si c’est possible.

Exemple :

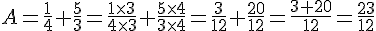
A=\frac{1 }{4}+\frac{5}{3}=\frac{1\times 3}{4\times 3 }+\frac{5\times 4 }{3\times 4}=\frac{3}{12}+\frac{20}{12}=\frac{3+20}{12}=\frac{23}{12}

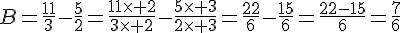
B=\frac{11}{3}-\frac{5}{2}=\frac{11\times 2}{3\times 2}-\frac{5\times 3}{2\times 3}=\frac{22}{6}-\frac{15}{6}=\frac{22-15}{6}=\frac{7}{6}

3) Multiplication de deux fractions :

Méthode :

Pour multiplier deux fractions, on multiplie les numérateurs entre eux et les dénominateurs entre eux.

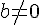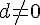On considère quatre nombres relatifs a,b,c et d tels que b\neq0 et  d\neq0.

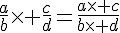
\frac{a}{b}\times \frac{c}{d}=\frac{a\times c}{b\times d}

Exemple :

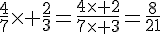
\frac{4}{7}\times \frac{2}{3}=\frac{4\times 2}{7\times 3}=\frac{8}{21}

Vous avez assimilé le cours sur les fractions en 5ème ?

Effectuez ce QCM de maths en cinquième sur les fractions afin d’évaluer vos acquis sur cette leçon.

Les fractions et le calcul fractionnaire

QCM sur les fractions et le calcul fractionnaire en cinquième.

4.6/5 - (29106 votes)
Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «fractions : cours de maths en 5ème en PDF.» au format PDF.

Ressources de cinquième

Cours de cinquième

Les fractions : cours de maths en 5ème
Fractions
Les triangles : cours de maths en 5ème
Les triangles et son cercle circonscrit et l’inégalité triangulaire
Droites remarquables du triangle : cours de maths en 5ème
Droites remarquables du triangle
Symétrie centrale : cours de maths en 5ème
Symétrie centrale et centre de symétrie
Parallélogramme : cours de maths en 5ème
Le parallélogramme
Angles : cours de maths en 5ème
Les angles correspondants et alternes-internes

Exercices de cinquième

exercices maths 5ème
Calcul littéral
exercices maths 5ème
Symétrie centrale
exercices maths 5ème
Angles
exercices maths 5ème
Nombres relatifs
exercices maths 5ème
Proportionnalité
exercices maths 5ème
Statistiques
×12

L'équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs
200+ Années cumulées
Quotidien Mise à jour

Nos ressources pédagogiques

📚 Les cours ✏️ Les exercices 🎓 Brevet 🏆 Bac
Nos applications

Téléchargez gratuitement la dernière version de nos applications.
Application Mathovore sur Google Play Store. Application Mathovore sur Apple Store.

Inscription gratuite à Mathovore.  Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.