Vecteurs et translation : corrigé des exercices de maths en 2de en PDF.
Mis à jour le 13 septembre 2025
Exercice 1 :
Les points P, Q et R sont-ils alignés ?
Oui ils sont alignés, montrez que les vecteurs 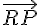 et
et 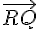 sont colinéaires
sont colinéaires
Exercice 2 :
ABCD est un parallélogramme.
I est le milieu de [AB].
E est le point tel que 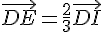
1. Effectuer la figure suivante.
3. Les points A, E et C sont-ils alignés ?
Oui ils sont alignés, montrez que les vecteurs 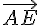 et
et 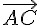 sont colinéaires.
sont colinéaires.
Exercice 3 :
A et B sont deux points distincts du plan .
On définit le point M par la relation vectorielle suivante :
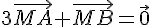 .
.
1. Exprimer 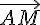 en fonction de
en fonction de  .
.
Utilisons la relation de Chasles :
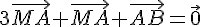

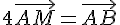
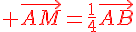
2. Placer le point M .
Exercice 4 :
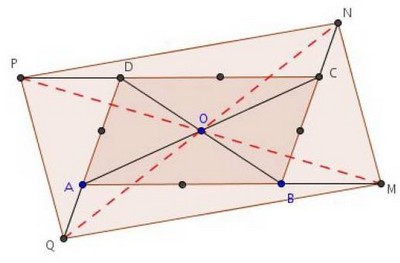
ABCD est un parallélogramme de centre O. Les points M, N, P et Q sont tels que :
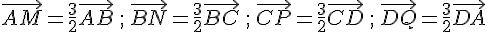
1.
a. Démontrer que 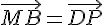 .
.
Nous avons :

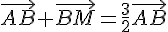


de même :
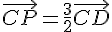
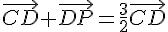

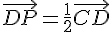
Or ABCD est un parallélogramme donc 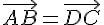
donc 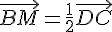
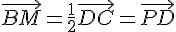
ainsi :
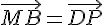
On en déduit que le quadrilatère MBPD est un parallélogramme.
b. Déduisez-en que O est le milieu de [MP] .
Propriété : les diagonales d’un parallélogramme se coupent en leur milieu.
Conclusion :
Le point O est le milieu de [MP].
Exercice 5 :
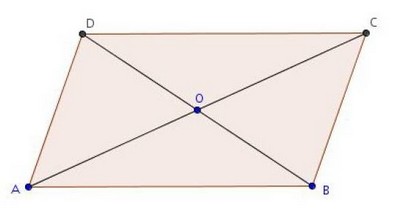
ABCD est un parallélogramme de centre O.
Donner l’ensemble des relations vectorielles possibles sur cette figure.
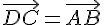
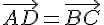
il y en a d’autres sur l’identité du parallélogramme
que vous aurez l’occasion de rencontrer dans d’autres exercices du site.
(O,I,J) est un repère orthonormal avec OI=OJ=1 cm.
a. Placer les points.
b. Nous avons :
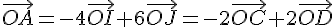
car 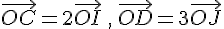
Les coordonnées de A(-2;2) dans (O,C,D)
de même, montrer que les coordonnées sont B(-1;-1) dans (O,C,D).
Dans le repère (O,D,C), il suffit d’inverser abscisse et ordonnée.
c. LE point O a pour coordonné O(1;1) dans le repère (E,C,D).
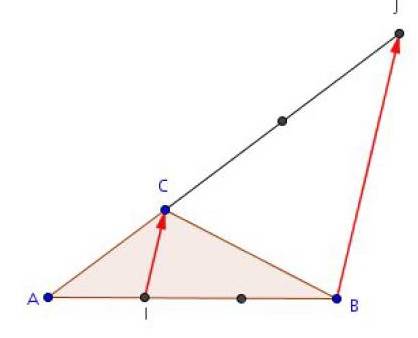
Exercice 7 :
La figure ci-dessous représente des hexagones réguliers de centres a, b, c, d.
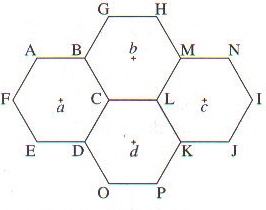
1. Déterminer les images de chacun des points C,E,A,M par la translation de vecteur :
a. La translation de vecteur  envoie C en L, E en D, A en B et M en N.
envoie C en L, E en D, A en B et M en N.
b. La translation de vecteur 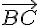 envoie C en d, A en a et M en c.
envoie C en d, A en a et M en c.
c. LA translation de vecteur 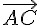 envoie C en K, E en O,A en C et M en I.
envoie C en K, E en O,A en C et M en I.
2. Utiliser la translation de vecteur 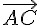
Exercice 8 :
Démontrer que pour tous points A, B, C, D.
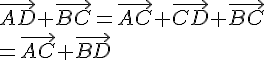 .
.
D’après la relation de Chasles.
Exercice 9 :
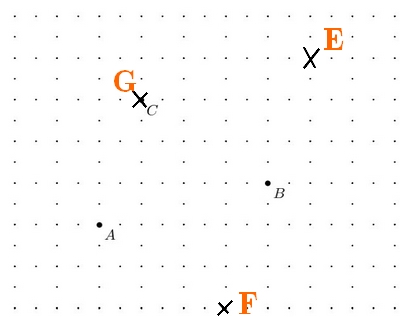
Dans un repère, on considère les points A(-5;3), B(2;-1), C(0;4).
a. Placer les points A,B,C.
b.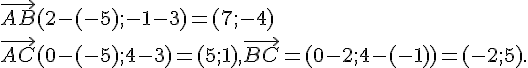 .
.
e.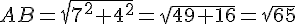 .
.
Exercice 11 :
1.
a. Avec GEOGEBRA, on peut construire le triangle ABC, ses milieux A’, B’ et C’, ainsi que son centre de gravité G et son centre de cercle circonscrit O.
On peut ensuite construire le point H en ajoutant les vecteurs OA, OB et OC.
b. On sait que le centre de gravité G est le point d’intersection des médianes,
donc on peut écrire :
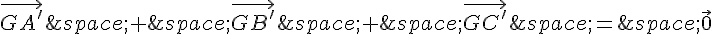
En multipliant cette équation par 2, on obtient :
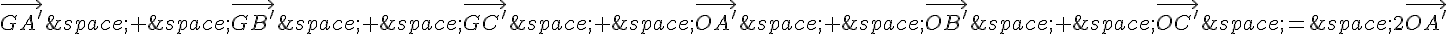
Or, on a :
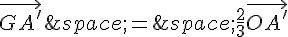
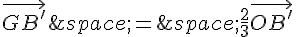
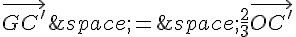
Donc :
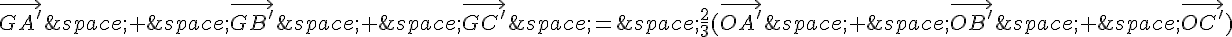
Et donc :
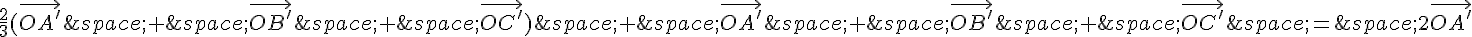
En simplifiant, on trouve :
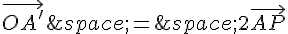
Donc :
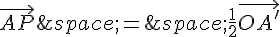
c. On a :
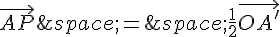
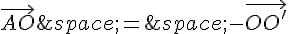
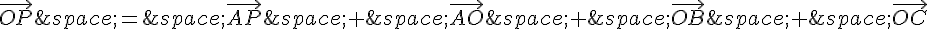
En remplaçant 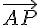 et
et  par les expressions trouvées précédemment, on obtient :
par les expressions trouvées précédemment, on obtient :
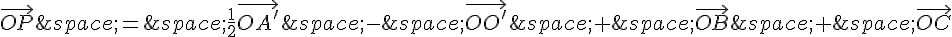
En simplifiant, on trouve :
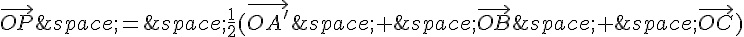
On sait que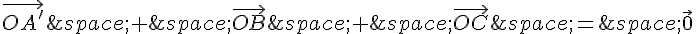 car les vecteurs représentant les côtés d’un triangle se fermant sur lui-même sont égaux à
car les vecteurs représentant les côtés d’un triangle se fermant sur lui-même sont égaux à 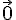 .
.
Donc :
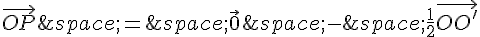
Et donc :
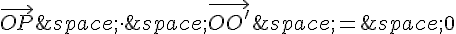
Mais 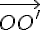 est un vecteur perpendiculaire au plan du triangle, donc il est orthogonal à tous les vecteurs appartenant à ce plan.
est un vecteur perpendiculaire au plan du triangle, donc il est orthogonal à tous les vecteurs appartenant à ce plan.
En particulier, il est orthogonal au vecteur 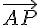 , donc (AP) est perpendiculaire à (BC).
, donc (AP) est perpendiculaire à (BC).
d. On peut montrer de même que (BP) est perpendiculaire à (AC) en utilisant les mêmes calculs.
e. Le point H est le point de Steiner, c’est-à-dire le centre du cercle circonscrit au triangle formé par les pieds des hauteurs du triangle ABC.
2. On a montré que :
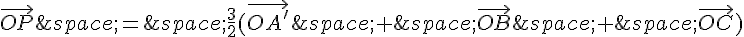

Donc :
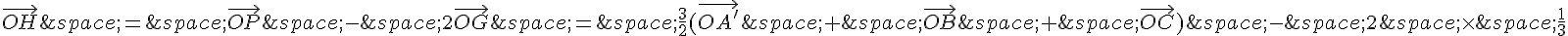
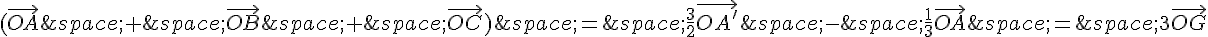
Donc 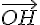 est trois fois plus grand que
est trois fois plus grand que 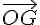 .
.
Cela signifie que le centre de gravité se trouve sur la droite d’Euler, car c’est le point qui divise la distance entre le centre du cercle circonscrit et le point de Steiner dans le rapport 2:1 (c’est-à-dire que OH est trois fois plus grand que OG).
Exercice 12 :
Analyse de la figure et remarques préliminaires.
(ME) est la droite des milieux donc (ME) et (BC) sont parallèles et 2.ME = BC. On en déduit que ME = BF = FC
(AF) est l’ axe de symétrie du triangle isocèle BAC donc (AF) est perpendiculaire à [BC] et [ME]
Dans le triangle AMC, [ME] est une médiane. Le centre de gravité G du triangle AMC est sur [ME] et l’on a : MG = 2.GE.
Démonstration
Considérons le quadrilatère MECF. Les cotés opposés [ME] et[CF] sont parallèles et isométriques. MECF est donc un parallélogramme; les diagonales [MC] et [EF] ont même milieu I.
Dans le triangle MEF, [MI] est une médiane, une autre médiane est portée par la droite (AF), il s’ensuit que le point D , intersection de deux médianes est le centre de gravité du triangle MEF.
Ainsi l’on a : 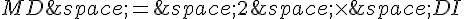 .
.
Considérons alors le triangle MEI, d’une part les points M , G , E sont alignés dans cet ordre, ainsi que les points M , D , I, et d’autre part on a les relations :
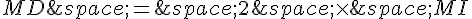 et
et 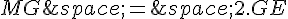
Il s’ensuit d’après la réciproque du théorème de Thalès que les droites (GD) et (IE) sont parallèles.
F étant le milieu de [BC] et E le milieu de [AC] alors [EF] est parallèle à [AB]. Ainsi la droite (MO) médiatrice de [AB] est perpendiculaire à [GD].(car (MO) est perpendiculaire à [EF] donc à [EI] et par suite à [GD])
Considérons finalement le triangle MGD
(DO) est perpendiculaire à [ME] et (MO) est perpendiculaire à (GD), il s’ensuit que O apparaît comme l’orthocentre du triangle MGD. La troisième hauteur étant portée par la droite (OG).
Conclusion :
Les droites (OG) et (MC) sont perpendiculaires.
Exercice 13 :
Désignons par A’ le point diamétralement opposé au point A. Il s’ensuit alors que les deux angles 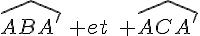 sont droits ( angles inscrits dans un demi-cercle )
sont droits ( angles inscrits dans un demi-cercle )
Puisque les droites (BH) et (A’C) sont perpendiculaires à la droite (AC) alors elles sont parallèles. Il en est de même des droites (BA’) et (CH) qui sont perpendiculaires à la droite (AB).
Ainsi le quadrilatère BHCA’ est un parallélogramme puisque ses côtés opposés sont parallèles deux à deux.
On sait que les diagonales d’un parallélogramme se coupent en leur milieu, donc [HA’] [BC] = {M}. Ainsi le milieu M de [BC] appartient aussi à la droite (A’H).
Conséquences:
Les droites (A’H) et (MH) sont confondues. Les points A’ , M , H , I sont donc alignés. Il en résulte que l’angle 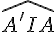 est droit puisqu’il est inscrit dans un demi-cercle.
est droit puisqu’il est inscrit dans un demi-cercle.
Les droites (MH) et (AI) sont donc perpendiculaires
Exercice 14 :
Dans un repère 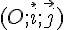 , on donne K ( – 3 ; 5) et L(4 ; 2).
, on donne K ( – 3 ; 5) et L(4 ; 2).
Déterminer l’abscisse du point M d’ordonnée – 2 tel que K, L et M soient alignés.
Pour que les points soient alignés il faut que les vecteurs 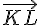 et
et 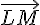 soient colinéaires avec
soient colinéaires avec 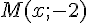 .
.
Calculons les coordonnées de ces deux vecteurs :
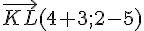
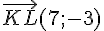
et

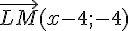
Ces deux vecteurs sont colinéaires si et seulement si :
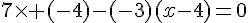
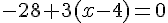
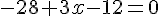
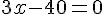
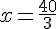
Conclusion : 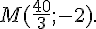
Exercice 15 :
Dans un repère 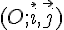 , on donne A(2 ;- 3) B(0 ; – 3) C( – 3 ; 0).
, on donne A(2 ;- 3) B(0 ; – 3) C( – 3 ; 0).
1. Déterminer par le calcul les coordonnées du point E tel que 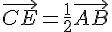 .
.
Résolvons un système :
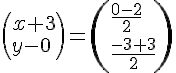
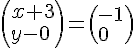
Nous obtenons les deux équations :
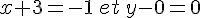 donc
donc
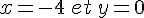
Conclusion : les coordonnées du point E sont E( – 4 ; 0 ) .
2. Que peut-on dire des droites (CE) et (AB) ? Justifier.
Les vecteurs 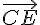 et
et  étant colinéaires, les droites (CE) et (AB) sont parallèles.
étant colinéaires, les droites (CE) et (AB) sont parallèles.
Exercice 16 :
Dans un repère 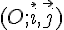 , on donne :
, on donne :
E(3 ; – 1) F(7 ; – 7) G(5 ; – 4).
Déterminer si les trois points E, F et G sont alignés.
Vérifions si les vecteurs 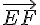 et
et 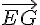 sont colinéaires alors les trois points seront alignés.
sont colinéaires alors les trois points seront alignés.
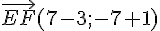 donc
donc 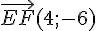
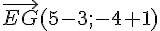 donc
donc 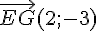
Nous remarquons que 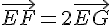 donc les vecteurs sont colinéaires
donc les vecteurs sont colinéaires
et les points E,F et G sont alignés.
Exercice 17 :
1. Les vecteurs 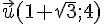 et
et 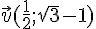 sont-ils colinéaires ?
sont-ils colinéaires ?
Calculons le déterminant :
Conclusion : ces deux vecteurs sont colinéaires.
2. Déterminer 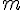 tel que les vecteurs
tel que les vecteurs 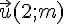 et
et 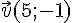 soient colinéaires.
soient colinéaires.
Le déterminant doit être nul :
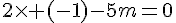
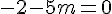
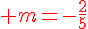
Exercice 18 :
Soient A, B, C et D, quatre points quelconques du plan.
Montrer que :
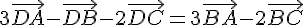
Nous avons
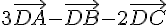
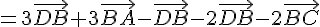


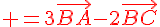
Exercice 19 :
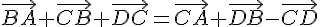
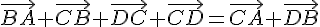
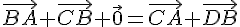
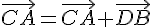
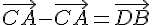
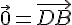
Conclusion : les points B et D sont confondus.
Exercice 20 :
A et B sont deux points distincts.
On cherche à construire le point M tel que :
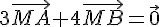
1. Les vecteurs 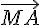 et
et 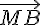 sont-ils colinéaires ?ont-ils le même sens?ont-ils la même norme?
sont-ils colinéaires ?ont-ils le même sens?ont-ils la même norme?
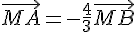
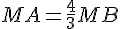
Conclusion : ces deux vecteurs sont colinéaires de sens opposés et n’ont pas la même norme.
2. En utilisant la relation de Chasles, montrer que l’on a l’égalité :
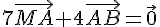
On sait que :
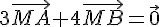

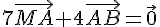
3. En déduire 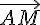 en fonction de
en fonction de  .
.
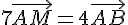
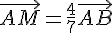
Construire le point M.
Exercice 21 :
Les vecteurs 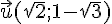 et
et 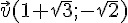 sont-ils colinéaires ?
sont-ils colinéaires ?
Calculons le déterminant :
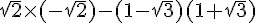
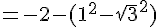
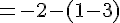
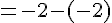
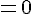
Conclusion : ces deux vecteurs sont bien colinéaires.
Exercice 22 :
On considère un triangle ABC et les points I et J tels que :
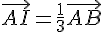
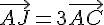
1. Montrer à l’aide de la relation de Chasles que 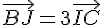 .
.
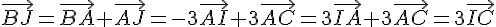
2. Que peut-on en déduire pour les droites (BJ) et (IC) ?
les vecteurs 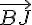 et
et 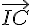 sont donc colinéaires et on en déduit que les droites (BJ) et (IC) sont parallèles.
sont donc colinéaires et on en déduit que les droites (BJ) et (IC) sont parallèles.
Exercice 23 :
Dans chacun des cas suivants, montrer que les vecteurs  et
et 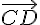 sont colinéaires.
sont colinéaires.
1. 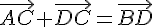 .
.
Utilisons la relation de Chasles :
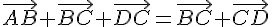
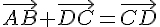
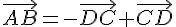
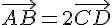
2. 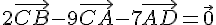
Utilisons la relation de Chasles
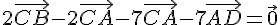
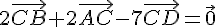
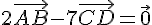
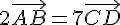
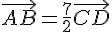
Exercice 24 :
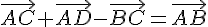 .
.
Utilisons la relation de Chasles :
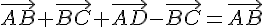
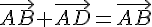
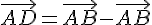
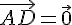
Conclusion : les points A et D sont confondus .
Exercice 25 :
1. Placer le point E tel que 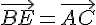 .
.
2. Placer le point F tel que 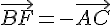 .
.
3. Placer le point G tel que 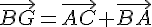 .
.
Exercice 30 :
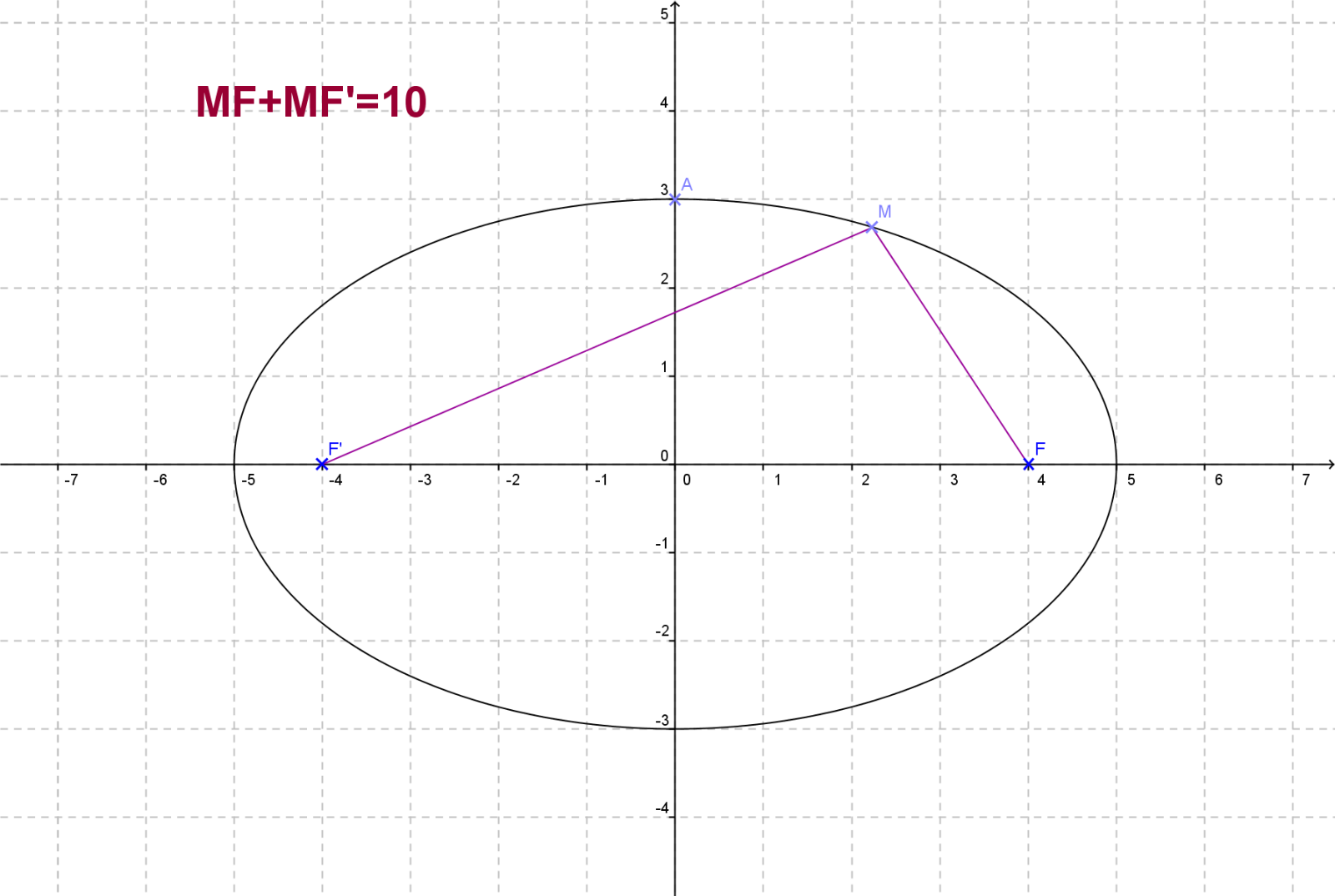
Dans le plan muni d’un repère orthonormé, on note E l’ensemble des points dont les coordonnées (x;y) vérifient la relation :
 .
.
On considère également les points F(4;0) et F'(-4;0).
1. Calculer les coordonnées des points d’intersection de E avec les axes du repères.
Lorsque x=0 , y=3 et y= -3.
Lorsque y=0, x=5 et x= – 5 .
2. A l’aide du logiciel Geogebra, visualiser l’ensemble E et faire une conjecture sur la somme des distances MF + MF’ lorsque M est un point de E.
La distance MF+MF’ est constante.
3. Soit M(x;y) un point de E.
a) Exprimer 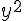 en fonction de
en fonction de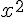 et en déduire que
et en déduire que 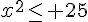 .
.

or  ce qui est équivalent à dire que
ce qui est équivalent à dire que 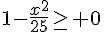 ce qui équivaut à
ce qui équivaut à 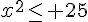
b) Montrer que 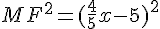 .
.
c) Sachant que 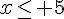 , montrer que
, montrer que 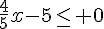
puis en déduire que 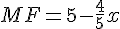 .
.
d) Valider la conjecture .
Exercice 31 :
Soit ABCD est un parallélogramme .
1) Placer les points M et N définis par les égalités suivantes:
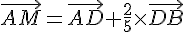
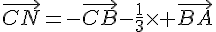
2) Montrer en utilisant la relation de Chasles que 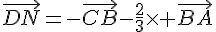 .
.
3) Exprimer le vecteur 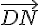 en fonction des vecteurs
en fonction des vecteurs 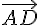 et
et 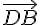 .
.
Indications :
Faire une figure et utiliser la relation de Chasles.
Exercice 32 :
1.a) Pour que ABCD soit un parallélogramme, il faut que les diagonales [AC] et [BD] se coupent en leur milieu en un point I. Pour trouver les coordonnées de D, on peut utiliser le fait que les diagonales d’un parallélogramme se coupent en leur milieu.
On a :
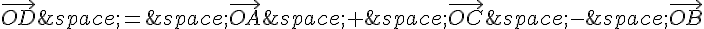
En utilisant les coordonnées de A, B et C, on trouve :

Donc les coordonnées de D sont (3, -1).
b) Le centre du parallélogramme est le milieu de ses diagonales, donc on peut calculer les coordonnées de I comme le milieu de AC et BD. On a :
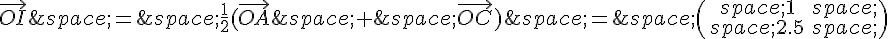
Donc les coordonnées de I sont (1, 2.5).
c) Pour trouver les coordonnées de F, on peut utiliser la formule donnant le symétrique d’un point par rapport à un autre :
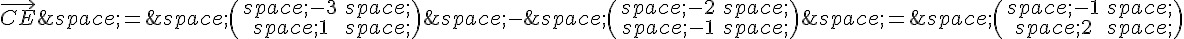
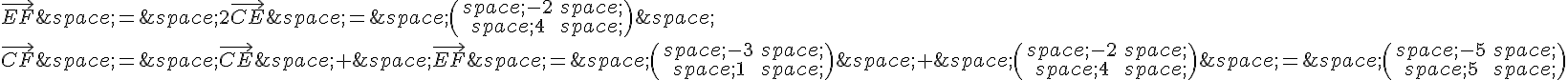
Donc les coordonnées de F sont (-5, 5).
d) Pour calculer les coordonnées de 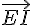 , on peut utiliser les coordonnées de E et de I :
, on peut utiliser les coordonnées de E et de I :
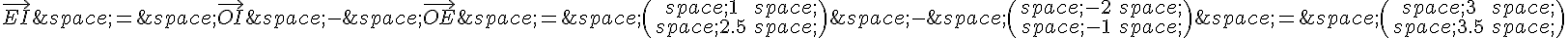
Pour calculer les coordonnées de 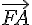 , on peut utiliser les coordonnées de F et de A :
, on peut utiliser les coordonnées de F et de A :
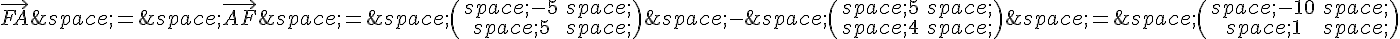
On remarque que les vecteurs 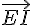 et
et 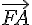 ont les mêmes coordonnées mais des signes opposés.
ont les mêmes coordonnées mais des signes opposés.
Cela n’est pas surprenant car dans un parallélogramme, les diagonales se coupent en leur milieu, donc le vecteur qui relie un sommet à ce point de coupure a un opposé qui relie l’autre sommet à ce point de coupure. On peut donc prévoir cette propriété.
2.
a) On sait que 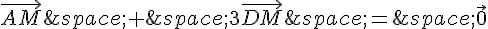 .
.
En utilisant les coordonnées de A et D, on trouve :
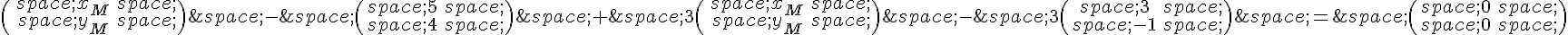
En développant et simplifiant, on trouve :
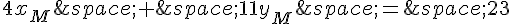
Donc les coordonnées de M sont 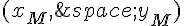 avec
avec  .
.
b) Pour savoir si les points M, I et D sont alignés, on peut calculer le coefficient directeur de la droite (MD) et celui de la droite (ID) et vérifier s’ils sont égaux.
Le coefficient directeur d’une droite passant par deux points (x1, y1) et (x2, y2) est donné par :
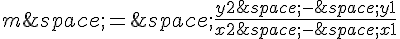
Le vecteur  a pour coordonnées :
a pour coordonnées :
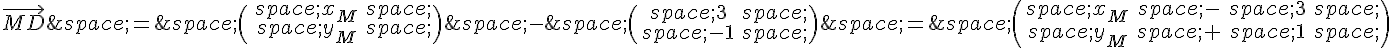
Le vecteur \vec{ID} a pour coordonnées :
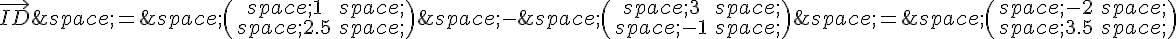
Le coefficient directeur de la droite (MD) est donc :
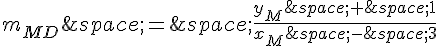
En substituant 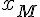 par son expression en fonction de
par son expression en fonction de 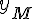 , on obtient :
, on obtient :
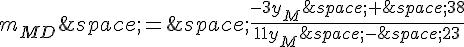
Le coefficient directeur de la droite (ID) est :
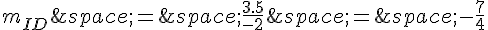
On remarque que les coefficients directeurs sont différents, donc les points M, I et D ne sont pas alignés.
Exercice 33 :
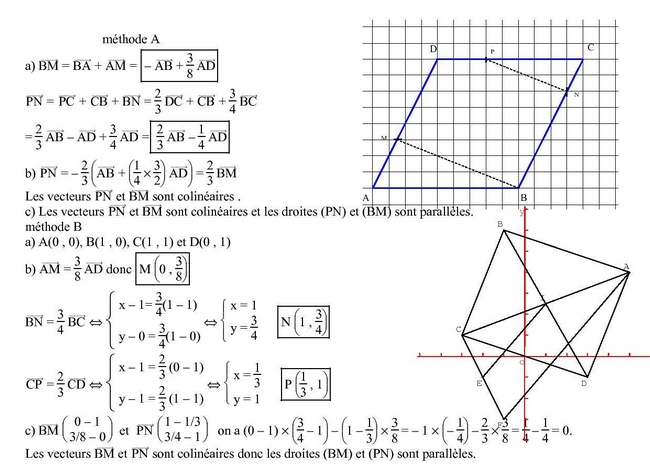
1.
a) Pour construire les points M, N et P, on peut tracer les vecteurs 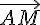 ,
, 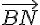 et
et 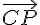 à partir des points A, B et C, dans les directions données par les coefficients des vecteurs. Les points M, N et P sont alors les extrémités de ces vecteurs.
à partir des points A, B et C, dans les directions données par les coefficients des vecteurs. Les points M, N et P sont alors les extrémités de ces vecteurs.
b) On peut exprimer les vecteurs 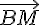 et
et 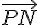 en fonction de
en fonction de  et
et 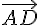 en utilisant les définitions de M et N :
en utilisant les définitions de M et N :

c) On remarque que 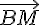 est une combinaison linéaire de
est une combinaison linéaire de  et
et 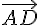 , c’est-à-dire qu’il est contenu dans le plan du parallélogramme, et de même pour
, c’est-à-dire qu’il est contenu dans le plan du parallélogramme, et de même pour 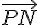 .
.
Si les deux vecteurs sont contenus dans le même plan et qu’ils ont des directions différentes, alors ils doivent être parallèles.
Donc (BM) et (PN) sont parallèles.
2.
a) Dans le repère 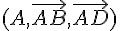 , les coordonnées des points A, B, C et D sont :
, les coordonnées des points A, B, C et D sont :
A(0, 0)
B(1, 0)
C(1, 1)
D(0, 1)
b) Pour calculer les coordonnées des points M, N et P, on peut utiliser les définitions données dans l’énoncé :
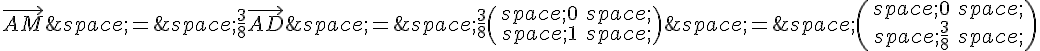
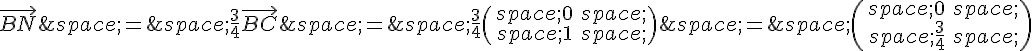
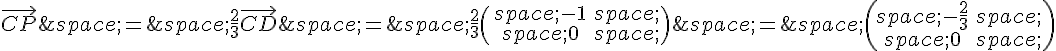
Donc les coordonnées de M, N et P sont :
M(0, 3/8)
N(1, 3/4)
P(1/3, 1)
c) Comme les points M et N sont situés sur la même droite verticale AB, et que le point P a une ordonnée plus grande que celle de N et une ordonnée plus petite que celle de M, alors les droites (BM) et (PN) doivent être parallèles.
Cela confirme le résultat obtenu avec la méthode A.
EXERCICE 34 :
1.a) Comme les droites (AB) et (DC) sont parallèles, on a 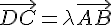 pour un certain
pour un certain 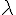 .
.
De plus, on sait que 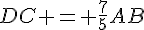 , donc
, donc 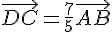 .
.
b) On peut exprimer 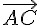 comme la somme de
comme la somme de  et
et 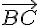 .
.
Comme ABCD est un trapèze, on a 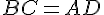 . Donc :
. Donc :
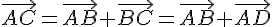
2)a) On sait que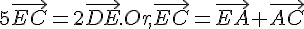 et
et 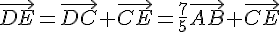 .
.
Donc :
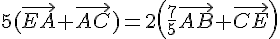
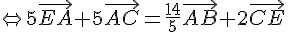
Comme ABCD est un trapèze, on a  , donc :
, donc :
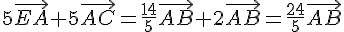
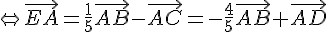
Finalement, on a 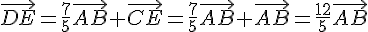 .
.
Pour placer le point E, on part de A, on avance dans la direction 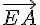 et on multiplie sa longueur par
et on multiplie sa longueur par 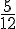 :
:
b) Les milieux de [AE] et [BD] sont respectivement M et N, tels que  .
.
Or, on sait que 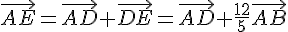 et
et 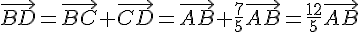 . Donc :
. Donc :
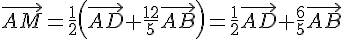
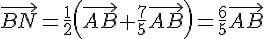
On veut montrer que 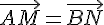 .
.
On a donc :
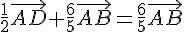
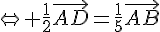
Ce qui est vrai, car  .
.
Donc :

3)a) On cherche x tel que 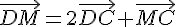 . Or, on sait que
. Or, on sait que 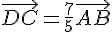 et
et 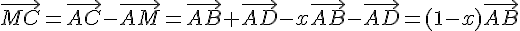 .
.
Donc :
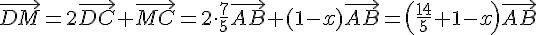
On veut que 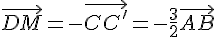 , donc :
, donc :
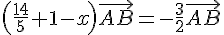
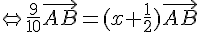

Donc, pour  , le point M est le symétrique de C par rapport à D.
, le point M est le symétrique de C par rapport à D.
b) On a 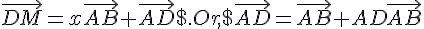 , donc :
, donc :
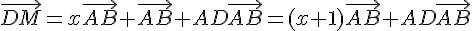
Le vecteur 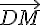 est une combinaison linéaire de
est une combinaison linéaire de  et de
et de 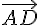 , qui sont tous deux fixes.
, qui sont tous deux fixes.
Donc le point M se déplace sur une droite. Cette droite est la parallèle à (AB) passant par le point D.
EXERCICE 35 :
1) En utilisant les relations données, on a:
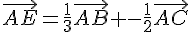

On peut donc construire les points E et F en partant de A, en prenant 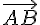 et
et 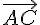 comme vecteurs directeurs et en ajoutant les vecteurs
comme vecteurs directeurs et en ajoutant les vecteurs 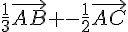 et
et 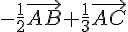 respectivement.
respectivement.
2) Calculons le vecteur 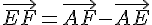 :
:
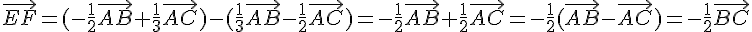
On en déduit que 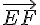 est colinéaire à
est colinéaire à 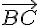 pour tout x de
pour tout x de  .
.
3) a) E = F si et seulement si 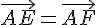 , ce qui donne:
, ce qui donne:
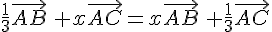
En développant cette équation, on obtient:
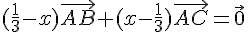
Cette équation est vérifiée si et seulement si les coefficients des vecteurs  et
et 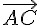 sont tous deux nuls, c’est-à-dire:
sont tous deux nuls, c’est-à-dire:
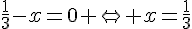
et
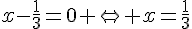
Donc E = F si et seulement si 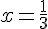 .
.
b) BCFE est un parallélogramme si et seulement si 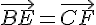 .
.
Or,
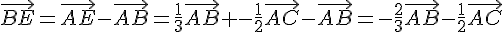
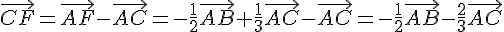
Donc 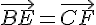 si et seulement si:
si et seulement si:
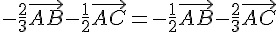
ce qui est équivalent à:
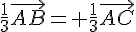
Cette équation est vérifiée si et seulement si le triangle ABC est équilatéral. Donc BCFE est un parallélogramme si et seulement si le triangle ABC est équilatéral.
EXERCICE 36 :
1) On a 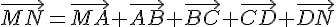 .
.
En utilisant les relations données, on a :
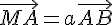
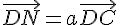
Donc 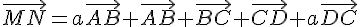
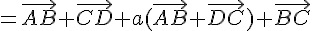
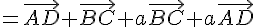
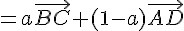
2) Si ABCD est un parallélogramme, alors 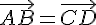 et
et 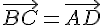 .
.
Donc, d’après la question précédente :
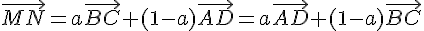
Donc 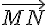 est une combinaison linéaire de
est une combinaison linéaire de 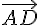 et
et 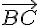 , c’est-à-dire qu’il est colinéaire à
, c’est-à-dire qu’il est colinéaire à 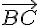 si et seulement si
si et seulement si 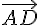 et
et 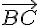 sont colinéaires.
sont colinéaires.
Or, dans un parallélogramme, cela est toujours vrai. Donc si ABCD est un parallélogramme, MBCN est un parallélogramme.
EXERCICE 37 :
1) En remplaçant a par 0 dans les relations données, on a :
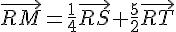
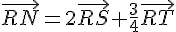

2) Calculons le vecteur 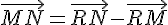 :
:
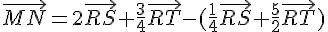

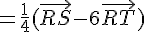
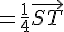
Donc 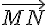 est colinéaire à
est colinéaire à 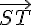 .
.
On peut en déduire que les vecteurs 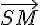 et
et 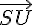 sont aussi colinéaires à
sont aussi colinéaires à 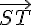 , car on peut les écrire comme des combinaisons linéaires de
, car on peut les écrire comme des combinaisons linéaires de 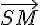 et
et 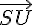 :
:
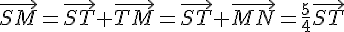
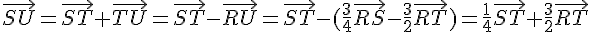
Donc SMTU est un parallélogramme, car les côtés opposés ont la même direction.
EXERCICE 38 :
1) On a 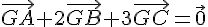 , donc :
, donc :
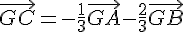
En utilisant les relations de Chasles, on a :
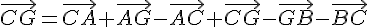
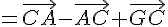
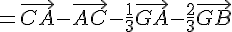
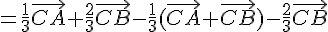
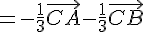
On peut donc construire G en traçant les vecteurs 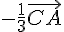 et
et 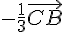 à partir des points A et B, puis en faisant leur somme à partir du point C.
à partir des points A et B, puis en faisant leur somme à partir du point C.
2) On a 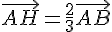 , donc :
, donc :
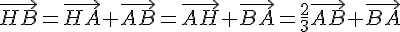
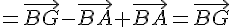
Donc H est le milieu de [AB]. En utilisant 1), on a :
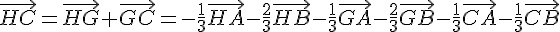
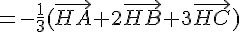

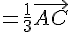
Donc G est bien le milieu de [HC].
3) En utilisant la question 1), on a :
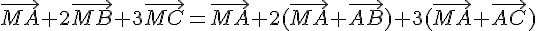
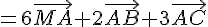
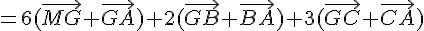
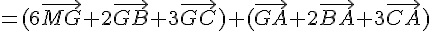
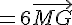
Donc pour tout point M, 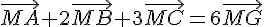 .
.
4)
a) On a 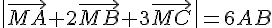 si et seulement si :
si et seulement si :
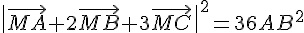
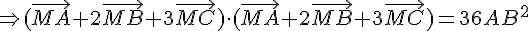
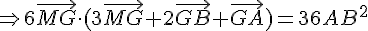
En utilisant la question 1), on peut exprimer  et
et 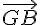 en fonction de
en fonction de 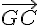 ,
,  et
et 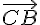 , et en utilisant la question 2), on peut exprimer
, et en utilisant la question 2), on peut exprimer 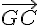 en fonction de
en fonction de  et
et 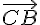 .
.
On obtient finalement :
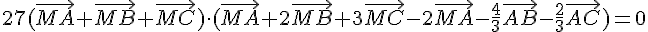

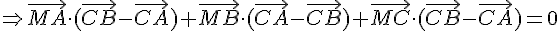
Donc l’ensemble des points M tels que 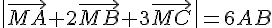 est la droite passant par les milieux des côtés AB, AC et BC.
est la droite passant par les milieux des côtés AB, AC et BC.
b) Le vecteur 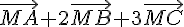 est colinéaire à
est colinéaire à 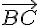 si et seulement si leur produit scalaire est nul :
si et seulement si leur produit scalaire est nul :
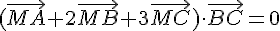
En développant et en utilisant les relations de Chasles, on obtient :
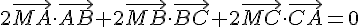
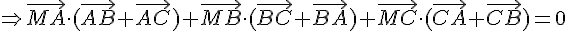

Donc l’ensemble des points M tels que 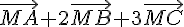 est colinéaire à
est colinéaire à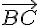 est la droite passant par le point G et parallèle à la droite (AB).
est la droite passant par le point G et parallèle à la droite (AB).
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «vecteurs et translation : corrigé des exercices de maths en 2de en PDF.» au format PDF.
Ressources de seconde
Cours de seconde
D'autres cours et exercices à consulter
🤖 Exercices IA Interactifs ✨

Des milliers d'exercices interactifs conformes aux programmes officiels. Apprenez, pratiquez et progressez à votre rythme.
Exercices interactifsL'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.




 .
.
.png)