Perpendiculaires 6e corrigé : droites parallèles et perpendiculaires

Sommaire

Perpendiculaires 6e corrigé : droites parallèles et perpendiculaires : corrigé des exercices de maths en 6ème en PDF.

De plus, Voici la correction complète des 32 exercices de la fiche consacrée aux droites parallèles et perpendiculaires. Chaque réponse est justifiée : on cite le codage de la figure, on énonce la propriété du cours utilisée, puis on conclut, exactement comme on l’attend d’un élève de sixième.

Les constructions sont expliquées étape par étape, avec la position de l’équerre, de la règle, du compas ou du rapporteur, et illustrées par des figures : perpendiculaires passant par un point, parallèle obtenue grâce à deux angles droits, passages menant d’une statue à trois allées, points communs à des segments, des demi-droites ou des droites. Puis les exercices de vocabulaire donnent les phrases complétées et les notations \(\in\) et \(\notin\), lues à voix haute.

Ce corrigé des droites perpendiculaires en 6e se consulte après avoir cherché seul : reprenez d’abord les énoncés des exercices sur les droites, puis vérifiez vos tracés et améliorez votre rédaction. Ensuite, les mesures d’angles lues sur une figure restent approximatives, à un ou deux degrés près.

Exercice 1 (perpendiculaires 6e corrigé)

1. Reproduire cette figure sur votre feuille, en respectant les mesures.

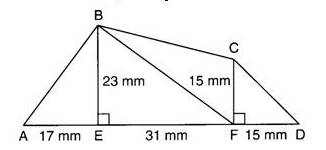
2. Démontrer que les droites (BE) et (CF) sont parallèles.
Les droites (BE) et (CF) sont perpendiculaires à une même droite (AD) donc elles sont parallèles entre elles.

Ensuite, on retrouve exactement la même méthode pour cet exercice. Ainsi, chaque étape se calcule de la même façon que précédemment. Donc il suffit d’appliquer le cours avec soin.

Exercice 2 :

On a réalisé et codé une figure :

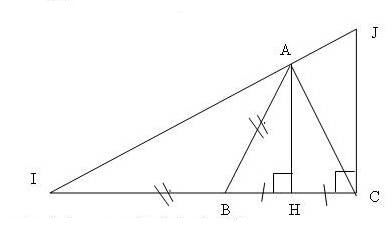
1. Citer des droites perpendiculaires à (IC).

D’après le codage, les droites (AH) et (JC) sont perpendiculaires à (IC).

2. D’après la figure, certaines droites semblent parallèles. Lesquelles ?

Les droites (AH) et (JC) semblent parallèles.

3. A l’aide d’une propriété du cours, justifier que ces deux droites sont parallèles.

On sait que : \((AH)\perp (IC)\) et \((JC)\perp (IC)\) (d’après le codage) .

Propriété :

Si deux droites sont perpendiculaires à une même droite, alors elles sont parallèles.

Conclusion :

Les droites (AH) et (JC) sont parallèles.

4. Compléter en utilisant les symboles\(\notin\) et \(\in\) .

a) A \(\in\) [IJ] b) I \(\notin\)[AJ] c) H \(\in\) [IB) d) J \(\in\) [IA).

De même, la démarche de cet exercice reste identique à celle des précédents. Par conséquent, on applique le même ordre de calcul. Enfin, on vérifie le résultat obtenu.

Exercice 3 (perpendiculaires 6e corrigé)

En observant les figures ci-dessous, compléter les phrases en utilisant les mots proposés :

a. Les droites (QR) et (FR) forment un angle droit.

b. La droite (LR) est la perpendiculaire à la droite (FQ) passant par le point T.

c. Les droites (LQ) et (TR) sont sécantes.

d. La droite (FR) semble parallèle à la droite (LQ).

e. La droite (RQ) semble être la parallèle à la droite (FL) passant par le point R.

f. La droite (AC) est perpendiculaire à la droite (BD).

g. Les droites (AC) et (DE) semblent parallèles entre elles.

h. La droite (AC) est la perpendiculaire à la droite (BD) passant par le point A.

Remarque : on écrit « la » perpendiculaire ou « la » parallèle lorsque la phrase précise le point par lequel passe la droite, car une seule droite convient. Puis les mots « une parallèle » et « une perpendiculaire » ne servent donc pas ici.

Ainsi, on applique ici le même raisonnement que pour l’exercice précédent. Donc les mêmes règles de calcul s’appliquent encore. Puis on simplifie le résultat si besoin.

Exercice 4 :

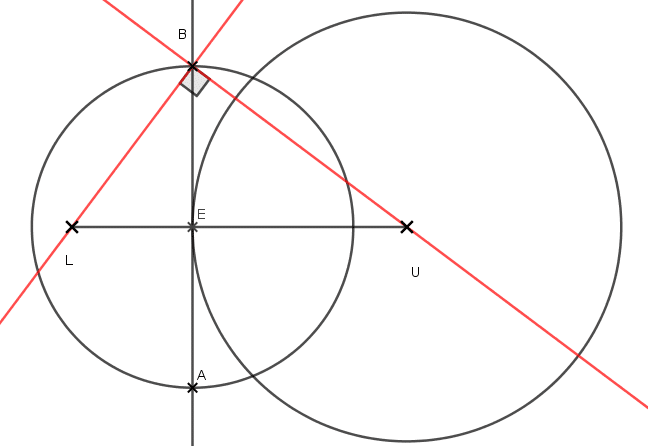
a. Voici la figure obtenue et il y a deux possibilités pour la position du point B.

b. (BL) et (BU) sont perpendiculaire car BLU est un triangle inscrit dans un demi-cercle donc c’est un triangle rectangle donc l’angle \(\widehat{LBU}\) est un angle droit.

Par ailleurs, cet exercice se traite avec la même technique de calcul. De ce fait, la vérification se fait de la même manière. Ainsi, chaque résultat reste facile à contrôler.

Exercice 5 (perpendiculaires 6e corrigé)

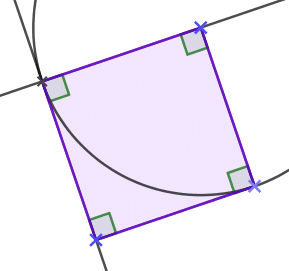
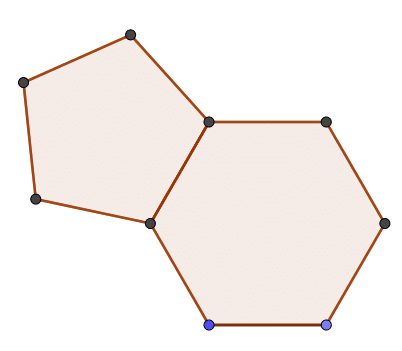
1.Nous obtenons un carré.

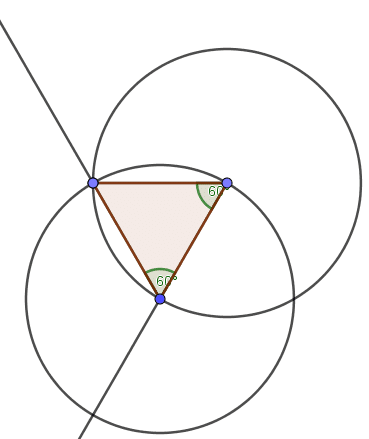
2.Nous obtenons un triangle équilatéral.

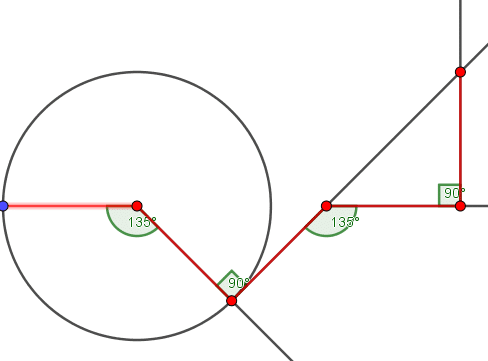
3. Voici le tracé du début de parcours qui est à réaliser 7 fois.

Également, on procède ici de la même façon que juste avant. Ainsi, on retrouve la même rigueur dans chaque étape. Donc rien ne change dans la méthode à suivre.

Exercice 6 :

Montrer que les droites (d1) et (d2) sont parallèles.

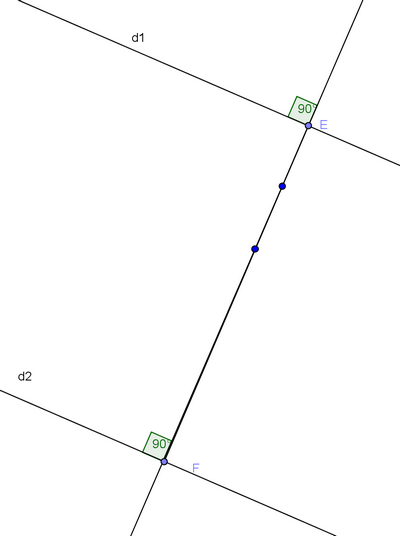
On sait que les droites (d1) et (d2) sont perpendiculaires à la même droite (EF)

Propriété : Si deux droites sont perpendiculaires à une même droite alors elles sont parallèles.

Conclusion : \((d_1)//(d_2)\).

Puis on continue avec un exercice qui se résout selon la même logique. Enfin, on vérifie chaque résultat avec soin. De plus, de plus, on prend le temps de bien rédiger.

Exercice 7 (perpendiculaires 6e corrigé)

Vous devez obtenir les tracés ci-dessous :

Ensuite, on retrouve exactement la même méthode pour cet exercice. Ainsi, chaque étape se calcule de la même façon que précédemment. Donc il suffit d’appliquer le cours avec soin.

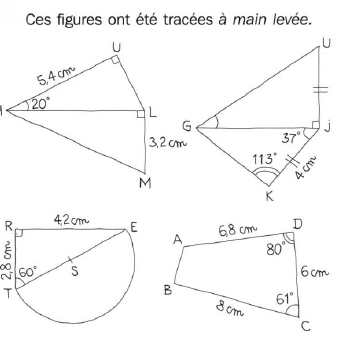
Exercice 8 :

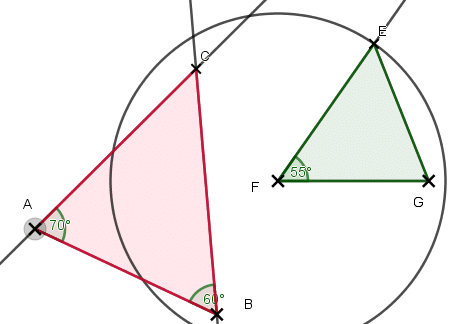
Tracer et mesurer ces angles à l’aide du rapporteur et du matériel de géométrie.

1. Mesurer des angles. On place le centre du rapporteur sur le sommet de l’angle et la graduation 0 sur l’un des côtés, puis on lit la mesure sur l’autre côté, en partant du 0 utilisé. Ainsi, de plus, les angles \(\hat{a}\), \(\hat{b}\), \(\hat{c}\) et \(\hat{e}\) sont aigus, l’angle \(\hat{d}\) est obtus. Sur la figure de l’énoncé, on trouve environ (à un ou deux degrés près, selon l’impression) :

\(\hat{e}\approx 16^\circ\) ; \(\hat{a}\approx 20^\circ\) ; \(\hat{c}\approx 49^\circ\) ; \(\hat{b}\approx 62^\circ\) ; \(\hat{d}\approx 123^\circ\).

Ainsi, Rangement dans l’ordre croissant : \(\hat{e}\lt\hat{a}\lt\hat{c}\lt\hat{b}\lt\hat{d}\).

2. Tracer des angles. Pour tracer \(\widehat{xOy}=15^\circ\) : on trace une demi-droite [Ox), on place le centre du rapporteur en O et le 0 sur [Ox), on marque un point à la graduation 15, puis on trace la demi-droite [Oy) passant par ce point. Ensuite, on procède de même pour les autres angles ; pour \(\widehat{ABC}=95^\circ\), \(\widehat{UCV}=120^\circ\), \(\widehat{MDN}=170^\circ\) et \(\widehat{VFW}=135^\circ\), on obtient des angles obtus, plus « ouverts » qu’un angle droit, et \(\widehat{xEz}=45^\circ\) est la moitié d’un angle droit.

Exercice 8 (suite)

3. Construire des triangles. Pour ABC : on trace [AB] de 6 cm, on construit en A un angle de 70° et en B un angle de 60°, du même côté de [AB] ; les deux demi-droites se coupent en C. Par ailleurs, on peut contrôler : \(\widehat{ACB}=180^\circ-70^\circ-60^\circ=50^\circ\). Puis pour EFG : on construit en F un angle de 55°, puis on reporte FE = 5 cm sur un côté et FG = 4,5 cm sur l’autre, et on trace [EG].

De même, la démarche de cet exercice reste identique à celle des précédents. Par conséquent, on applique le même ordre de calcul. Enfin, on vérifie le résultat obtenu.

Exercice 9 (perpendiculaires 6e corrigé)

Ainsi, on applique ici le même raisonnement que pour l’exercice précédent. Donc les mêmes règles de calcul s’appliquent encore. Puis on simplifie le résultat si besoin.

Exercice 10 :

Par ailleurs, cet exercice se traite avec la même technique de calcul. De ce fait, la vérification se fait de la même manière. Ainsi, chaque résultat reste facile à contrôler.

Exercice 11 (perpendiculaires 6e corrigé)

1. Ensuite, on reproduit la figure : on trace une droite (d), on place un point C sur cette droite, puis deux points A et B qui ne sont pas sur (d), A au-dessus de (d) à gauche et B à droite.

2. Méthode avec l’équerre : on place un côté de l’angle droit de l’équerre le long de la droite (d), puis on fait glisser l’équerre le long de (d) jusqu’à ce que l’autre côté de l’angle droit passe par le point voulu. Puis on trace alors la droite, on la prolonge à la règle et on code l’angle droit.

a. Par A : l’équerre glisse le long de (d) jusqu’à ce que son deuxième côté passe par A. On obtient la perpendiculaire à (d) passant par A.
b. Par B : même méthode, de l’autre côté de C. On obtient la perpendiculaire à (d) passant par B.
c. Par C : le point C est sur (d), donc on place le sommet de l’angle droit de l’équerre exactement sur C. On obtient la perpendiculaire à (d) en C.

Remarque : les trois droites tracées sont perpendiculaires à la même droite (d), donc elles sont parallèles entre elles.

Également, on procède ici de la même façon que juste avant. Ainsi, on retrouve la même rigueur dans chaque étape. Donc rien ne change dans la méthode à suivre.

Exercice 12 :

On reproduit la figure, puis on utilise l’équerre comme à l’exercice 11 : un côté de l’angle droit contre la droite, l’autre côté passant par le point.

a. Par le point S, on trace la perpendiculaire à \((d_1)\) et la perpendiculaire à \((d_2)\). De plus, ce sont deux droites différentes, car \((d_1)\) et \((d_2)\) sont sécantes : elles n’ont pas la même direction.

b. Par le point T, on trace de même la perpendiculaire à \((d_1)\) et la perpendiculaire à \((d_2)\).

Remarque : les deux perpendiculaires à \((d_1)\) (celle qui passe par S et celle qui passe par T) sont parallèles entre elles, car elles sont perpendiculaires à la même droite. Ensuite, il en est de même pour les deux perpendiculaires à \((d_2)\).

Puis on continue avec un exercice qui se résout selon la même logique. Enfin, on vérifie chaque résultat avec soin. De même, de plus, on prend le temps de bien rédiger.

Exercice 13 (perpendiculaires 6e corrigé)

Sur la figure, la droite (AB) passe par A, O et B, avec O entre A et B. Par ailleurs, la droite (CD) passe par C, D et O, dans cet ordre : D est entre C et O.

a. Les points A et O sont sur la droite (AB), mais D n’est pas sur (AB) : les deux droites n’ont que le point O en commun. Faux : A, O et D ne sont pas alignés.
b. O est sur la droite (AB), entre A et B. Vrai : \(O\in[AB]\).
c. La demi-droite [DC) a pour origine D et passe par C : elle part de D vers la gauche. Le point O est de l’autre côté de D. Faux : \(O\notin[DC)\) (en revanche \(O\in[CD)\)).
d. Le seul point commun possible des deux segments serait O, car c’est le seul point commun des droites (AB) et (CD). Or O n’appartient pas au segment [CD], puisqu’il est au-delà de D. Vrai : les segments [AB] et [CD] n’ont aucun point commun.
e. Les droites (AB) et (CD) se coupent en O. Vrai.

Ensuite, on retrouve exactement la même méthode pour cet exercice. Ainsi, chaque étape se calcule de la même façon que précédemment. Donc il suffit d’appliquer le cours avec soin.

Exercice 14 :

Les points sont alignés dans l’ordre A, M, N, P, B.

a. \(M\in[AB]\) : « M appartient au segment [AB] », car M est entre A et B.
b. \(P\notin[MN]\) : « P n’appartient pas au segment [MN] », car P n’est pas entre M et N.
c. \(B\in(AN)\) : « B appartient à la droite (AN) », car les cinq points sont sur la même droite.
d. \(N\in(BP)\) : « N appartient à la droite (BP) ».
e. \(M\in[AN]\) : « M appartient au segment [AN] », car M est entre A et N.
f. \(A\notin[PN]\) : « A n’appartient pas au segment [PN] », car A n’est pas entre P et N.

De même, la démarche de cet exercice reste identique à celle des précédents. Par conséquent, on applique le même ordre de calcul. Enfin, on vérifie le résultat obtenu.

Exercice 15 (perpendiculaires 6e corrigé)

On lit sur la figure : \((d_1)\) passe par A, B et C ; \((d_2)\) passe par D, F et C ; \((d_3)\) passe par E, F et B ; \((d_4)\) passe par A, D et E.

a. Les droites \((d_1)\) et \((d_2)\) se coupent en C.
b. Le point commun aux droites \((d_3)\) et \((d_4)\) est E.
c. D est le point commun aux droites \((d_2)\) et \((d_4)\).
d. Les droites \((d_2)\) et \((d_3)\) se coupent au point F (elles sont sécantes en F).
e. A est le point commun aux droites \((d_1)\) et \((d_4)\).

Ainsi, on applique ici le même raisonnement que pour l’exercice précédent. Donc les mêmes règles de calcul s’appliquent encore. Puis on simplifie le résultat si besoin.

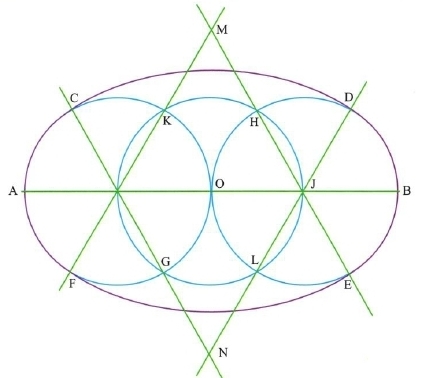
Exercice 16 :

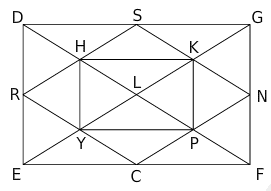
Dans cette figure, les droites qui semblent perpendiculaires ou parallèles, le sont réellement.

De plus, la droite perpendiculaire à (HK) passant par H est la droite (HY) .
La droite perpendiculaire à (CE) passant par N est la droite (NF).
La droite parallèle à (HP) passant par N est la droite (NS).
La droite parallèle à (CF) passant par S est la droite (SG).
La droite parallèle à (PN) passant par R est la droite (RS) .

Par ailleurs, cet exercice se traite avec la même technique de calcul. De ce fait, la vérification se fait de la même manière. Ainsi, chaque résultat reste facile à contrôler.

Exercice 17 (perpendiculaires 6e corrigé)

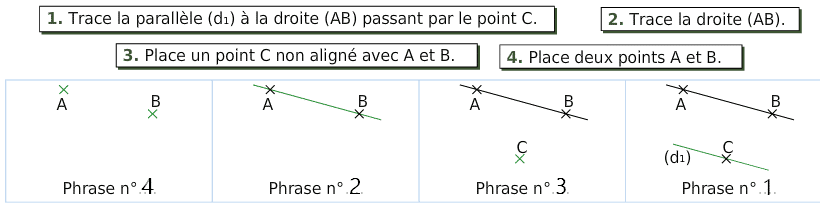
Pour chaque étape de la construction, choisir, parmi les phrases suivantes, celle qui convient.

Les phrases proposées sont :

Trace la parallèle \((d_1)\) à la droite (AB) passant par le point C.
Trace la droite (AB).
Place un point C non aligné avec A et B.
Place deux points A et B.

Ainsi, étape 1 (on ne voit que les points A et B) : phrase n° 4.
Étape 2 (la droite (AB) apparaît) : phrase n° 2.
Étape 3 (le point C apparaît, hors de (AB)) : phrase n° 3.
Étape 4 (la droite \((d_1)\) parallèle à (AB) passe par C) : phrase n° 1.

L’ordre du programme de construction est donc : 4 ; 2 ; 3 ; 1.

Également, on procède ici de la même façon que juste avant. Ainsi, on retrouve la même rigueur dans chaque étape. Donc rien ne change dans la méthode à suivre.

Exercice 18 :

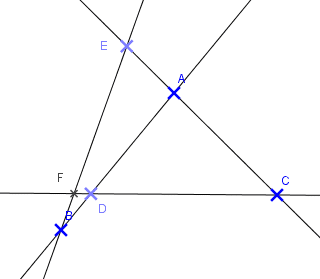
a) Placer trois points A, B et C non alignés.
b) Tracer la droite (AB).
c) Placer les points D, E et F tels que :

D \(\in\) (AB) et D \(\in\) [AB] ;
E \(\in\) (AC) et E \(\in\)[CA) ;
De même, F \(\in\) (BE) et F \(\in\) (CD).

Puis on continue avec un exercice qui se résout selon la même logique. Enfin, on vérifie chaque résultat avec soin. Également, de plus, on prend le temps de bien rédiger.

Exercice 19 (perpendiculaires 6e corrigé)

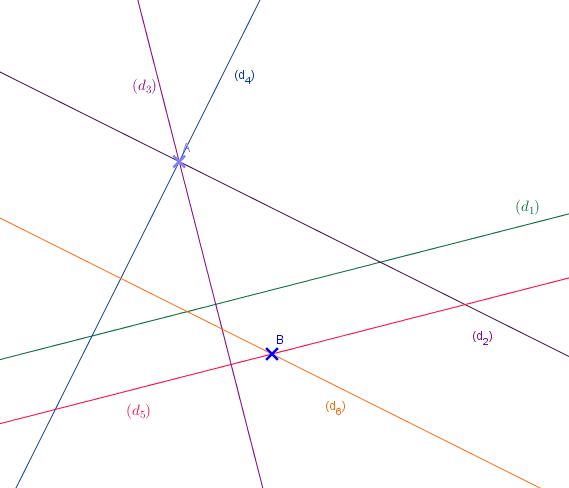
Tracer la droite (d₃) perpendiculaire à la droite (d₁) passant par le point A.
Tracer la droite (d₄) perpendiculaire à la droite (d₂) passant par le point A.
Tracer la droite (d₅) parallèle à la droite (d₁) passant par le point B.
Tracer la droite (d₆) parallèle à la droite (d₂) passant par le point B.

Ensuite, on retrouve exactement la même méthode pour cet exercice. Ainsi, chaque étape se calcule de la même façon que précédemment. Donc il suffit d’appliquer le cours avec soin.

Exercice 20 :

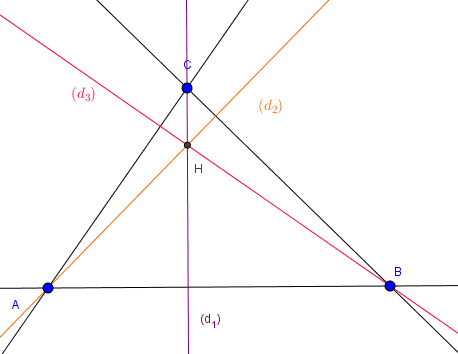
A, B et C sont trois points non alignés.

Tracer la droite (d1) perpendiculaire à (AB) passant par C.
Tracer la droite (d2) perpendiculaire à (BC) passant par A.
Tracer la droite (d3) perpendiculaire à (AC) passant par B.
Comment sont les droites (d1), (d2) et (d3) ?

4. Puis en traçant soigneusement les trois perpendiculaires à l’équerre, on constate qu’elles passent toutes par un même point, noté H sur la figure. Les droites (d1), (d2) et (d3) sont concourantes en H.

De même, la démarche de cet exercice reste identique à celle des précédents. Par conséquent, on applique le même ordre de calcul. Enfin, on vérifie le résultat obtenu.

Exercice 21 (perpendiculaires 6e corrigé)

a. Ensuite, on place les quatre points comme sur le modèle : M et N en haut, S et T en bas, M au-dessus de S et N à gauche de T.

b. Puis les segments [MT] et [SN] relient chacun un point du haut à un point du bas situé de l’autre côté : ce sont les « diagonales » du quadrilatère MNTS. Oui, ils se coupent, et on note P leur point commun.

c. De plus, les droites (MN) et (ST) ne sont pas parallèles : (MN) descend légèrement vers la droite alors que (ST) monte légèrement vers la droite, donc l’écart entre elles diminue. Par ailleurs, comme une droite est illimitée, il suffit de les prolonger. Oui, elles se coupent en un point R situé loin à droite, au-delà de N et de T (il faut prolonger nettement les deux droites pour le voir).

Ainsi, on applique ici le même raisonnement que pour l’exercice précédent. Donc les mêmes règles de calcul s’appliquent encore. Puis on simplifie le résultat si besoin.

Exercice 22 :

a. Ensuite, on reproduit la figure sur le quadrillage en comptant les carreaux à partir du coin en bas à gauche : P est à 1 carreau vers la droite et 1 carreau vers le haut, L à 2 carreaux vers la droite et 3 vers le haut, O à 4 vers la droite et 4 vers le haut, U à 5 vers la droite et 2 vers le haut.

b. Par ailleurs, le segment [LO] est entièrement situé au-dessus du segment [PU] : les droites (LO) et (PU) ne se couperaient que bien plus loin, en bas à gauche, en dehors des deux segments. Non, les segments [LO] et [PU] ne se coupent pas.

Exercice 22 (suite)

c. Puis la demi-droite [PL) part de P et monte vers la droite en passant par L ; la demi-droite [UO) part de U et monte vers la gauche en passant par O. Ensuite, en les prolongeant au-delà de L et de O, elles se rencontrent. Oui, elles se coupent en un point T situé un carreau et demi au-dessus de O et trois quarts de carreau à sa gauche, c’est-à-dire juste au-dessus du quadrillage dessiné (il faut prolonger la feuille d’une ligne de carreaux).

Par ailleurs, cet exercice se traite avec la même technique de calcul. De ce fait, la vérification se fait de la même manière. Ainsi, chaque résultat reste facile à contrôler.

Exercice 23 (perpendiculaires 6e corrigé)

a. Puis ce que l’on voit sur le dessin ne sont que des morceaux des droites (UV) et (EF). Enfin, de plus, une droite est illimitée : il faut imaginer qu’elle se prolonge des deux côtés. Ensuite, la droite (EF) est horizontale, tandis que la droite (UV) monte vers la droite ; l’écart entre elles n’est donc pas constant, et elles ne sont pas parallèles. Par ailleurs, en les prolongeant vers la gauche, elles finissent par se couper. Ilyes n’a pas raison : les droites (UV) et (EF) sont sécantes (leur point commun est très loin à gauche, en dehors du dessin).

b. Puis on trace les droites (EU) et (FV) : elles se rapprochent vers le haut et se coupent au-dessus de la droite (UV). De plus, leur point commun est le point C. Ensuite, on trace ensuite les droites (UF) et (VE) : elles se croisent entre les deux droites de départ. Ainsi, leur point commun est le point P.

Également, on procède ici de la même façon que juste avant. Ainsi, on retrouve la même rigueur dans chaque étape. Donc rien ne change dans la méthode à suivre.

Exercice 24 :

1. Puis on reproduit la figure : la droite (d), le point C sur (d), le point A au-dessus de (d) à gauche et le point B à droite.

2. De plus, pour chaque point, on place un côté de l’angle droit de l’équerre le long de (d) et on la fait glisser jusqu’à ce que l’autre côté passe par le point, puis on trace la droite et on code l’angle droit.

a. On obtient la perpendiculaire à (d) passant par A.
b. On obtient la perpendiculaire à (d) passant par B.
c. C est sur (d) : on place le sommet de l’angle droit de l’équerre en C et on obtient la perpendiculaire à (d) en C.

De même, les trois perpendiculaires sont parallèles entre elles, puisqu’elles sont toutes perpendiculaires à la droite (d).

Puis on continue avec un exercice qui se résout selon la même logique. Enfin, on vérifie chaque résultat avec soin. De même, de plus, on prend le temps de bien rédiger.

Exercice 25 (perpendiculaires 6e corrigé)

Pour chaque allée, on trace la perpendiculaire à l’allée qui passe par S : on place un côté de l’angle droit de l’équerre le long de l’allée et on la fait glisser jusqu’à ce que l’autre côté passe par S. Ensuite, le passage est le segment qui va de S jusqu’au point où cette perpendiculaire rencontre l’allée ; on code l’angle droit.

Un passage perpendiculaire à l’allée de la Cascade, vers le haut à gauche ;
un passage perpendiculaire à l’allée du Grand-Cèdre, vers le haut à droite ;
un passage perpendiculaire à l’allée des Cygnes, presque vertical, vers le bas.

Chaque passage ainsi tracé est aussi le chemin le plus court entre la statue et l’allée.

Ensuite, on retrouve exactement la même méthode pour cet exercice. Ainsi, chaque étape se calcule de la même façon que précédemment. Donc il suffit d’appliquer le cours avec soin.

Exercice 26 :

Dans les deux cas, on utilise la méthode des deux angles droits :

avec l’équerre, on trace la droite perpendiculaire à (d) passant par A (en pointillés sur la figure) ;
toujours avec l’équerre, on trace la droite perpendiculaire à ces pointillés passant par A : c’est la droite (d’).

Justification : les droites (d) et (d’) sont perpendiculaires à une même droite, donc elles sont parallèles. La droite (d’) passe par A et est parallèle à (d).

On peut aussi faire glisser l’équerre le long d’une règle posée perpendiculairement à (d) : un côté de l’équerre reste alors parallèle à (d).

De même, la démarche de cet exercice reste identique à celle des précédents. Par conséquent, on applique le même ordre de calcul. Enfin, on vérifie le résultat obtenu.

Exercice 27 :

1. Par ailleurs, on place les six points sur le quadrillage comme sur le modèle.

2. Notations et tracés :

a. Le segment d’extrémités A et B se note [AB] : on trace le segment de A à B, sans dépasser.
b. La droite passant par C et D se note (CD) : on trace une droite qui dépasse de part et d’autre de C et de D.
c. La demi-droite d’origine B passant par E se note [BE) : on la trace à partir de B, en passant par E et en la prolongeant au-delà de E seulement.
d. On trace la droite (EF) et on place un point I dessus : \(I\in(EF)\).

Ainsi, on applique ici le même raisonnement que pour l’exercice précédent. Donc les mêmes règles de calcul s’appliquent encore. Puis on simplifie le résultat si besoin.

Exercice 28 :

	Figure 1	Figure 2	Figure 3
Le point M … à la droite (AB)	appartient	appartient	n’appartient pas
Le point M … au segment [AB]	appartient	n’appartient pas	n’appartient pas
En langage mathématique	\(M\in(AB)\) et \(M\in[AB]\)	\(M\in(AB)\) et \(M\notin[AB]\)	\(M\notin(AB)\) et \(M\notin[AB]\)

Figure 1 : M est sur la droite, entre A et B, donc \(M\in(AB)\) et \(M\in[AB]\).
Figure 2 : M est sur la droite, mais au-delà de B, donc \(M\in(AB)\) et \(M\notin[AB]\).
Figure 3 : M n’est pas sur la droite, donc il n’est pas non plus sur le segment : \(M\notin(AB)\) et \(M\notin[AB]\).

Par ailleurs, cet exercice se traite avec la même technique de calcul. De ce fait, la vérification se fait de la même manière. Ainsi, chaque résultat reste facile à contrôler.

Exercice 29 :

Les points sont alignés dans l’ordre A, M, N, P, B.

a. \(M\in[AB]\) : « M appartient au segment [AB] ».
b. \(P\notin[MN]\) : « P n’appartient pas au segment [MN] », car P n’est pas entre M et N.
c. \(B\in(AN)\) : « B appartient à la droite (AN) ».
d. \(N\in(BP)\) : « N appartient à la droite (BP) ».
e. \(M\in[AN]\) : « M appartient au segment [AN] ».
f. \(A\notin[PM]\) : « A n’appartient pas au segment [PM] », car A n’est pas entre P et M.

Également, on procède ici de la même façon que juste avant. Ainsi, on retrouve la même rigueur dans chaque étape. Donc rien ne change dans la méthode à suivre.

Exercice 30 :

Sur la figure : \((d_1)\) passe par A, B et C ; \((d_2)\) passe par D, F et C ; \((d_3)\) passe par E, F et B ; \((d_4)\) passe par A, D et E.

a. Les droites \((d_1)\) et \((d_2)\) se coupent en C.
b. Le point commun aux droites \((d_3)\) et \((d_4)\) est E.
c. D est le point commun aux droites \((d_2)\) et \((d_4)\).
d. Les droites \((d_2)\) et \((d_3)\) se coupent au point F.
e. A est le point commun aux droites \((d_1)\) et \((d_4)\).

Puis on continue avec un exercice qui se résout selon la même logique. Enfin, on vérifie chaque résultat avec soin. Également, de plus, on prend le temps de bien rédiger.

Exercice 31 :

Sur la figure : \((d_1)\) passe par B, D et C ; \((d_2)\) passe par A, D et E ; \((d_3)\) passe par A et B ; \((d_4)\) passe par E et C, et le codage indique un angle droit en E entre \((d_2)\) et \((d_4)\).

a. Les droites \((d_1)\) et \((d_2)\) sont sécantes en D.
b. Le point d’intersection des droites \((d_2)\) et \((d_3)\) est A.
c. B est le point d’intersection des droites \((d_1)\) et \((d_3)\).
d. C est le point d’intersection des droites \((d_1)\) et \((d_4)\).
e. Les droites \((d_3)\) et \((d_4)\) sont sécantes : elles ne sont pas parallèles, donc en les prolongeant vers le haut elles se coupent, en dehors du dessin.
f. Les droites \((d_2)\) et \((d_4)\) sont perpendiculaires en E (d’après le codage de l’angle droit).

Ensuite, on retrouve exactement la même méthode pour cet exercice. Ainsi, chaque étape se calcule de la même façon que précédemment. Donc il suffit d’appliquer le cours avec soin.

Exercice 32 :

On sait que, d’après le codage, \((d_1)\perp(d)\) et \((d_2)\perp(d)\).

Propriété : si deux droites sont perpendiculaires à une même droite, alors elles sont parallèles entre elles.

Également, Conclusion : \((d_1)//(d_2)\). Emma a raison : les droites \((d_1)\) et \((d_2)\) sont parallèles. Elle ne se fie pas seulement à l’impression visuelle : c’est le codage des deux angles droits qui permet de l’affirmer.

Perpendiculaires 6e corrigé : nos conseils pour progresser

D’abord, cherche chaque exercice seul, sur une feuille de brouillon. Ensuite, compare ta démarche avec la correction, étape par étape. De cette façon, tu comprends d’où vient chaque erreur. Par ailleurs, perpendiculaires 6e corrigé en sixième demande surtout de la régularité.

Par exemple, explique la méthode à voix haute, comme à un camarade. Enfin, si tu veux approfondir, consulte la page Droite (mathématiques) sur Wikipédia. Également, tu peux continuer avec construction de figures géométriques : corrigé des exercices en 6ème en PDF.

4.8/5 - (31689 votes)

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «droites parallèles et perpendiculaires : corrigé des exercices de maths en 6ème en PDF.» au format PDF.