Triangles et quadrilatères avec constructions : corrigé en 6ème.

Corrigé des exercices de maths en 6ème sur le triangle et les quadrilatères avec des constructions de figures géométriques. Savoir utiliser son matériel de géométrie (règle, compas, rapporteur et équerre).

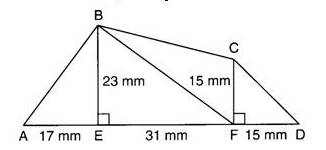
Exercice 1 :

2. Les droites (BE) et (CF) sont perpendiculaires à une même droite (AD) donc elles sont parallèles entre elles.

Exercice 2 :

Exercice 3 :

Exercice 4 :

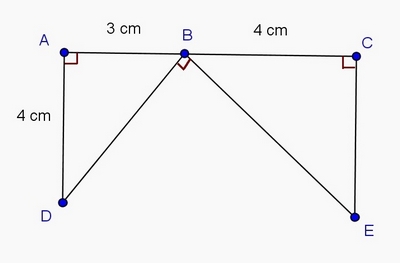
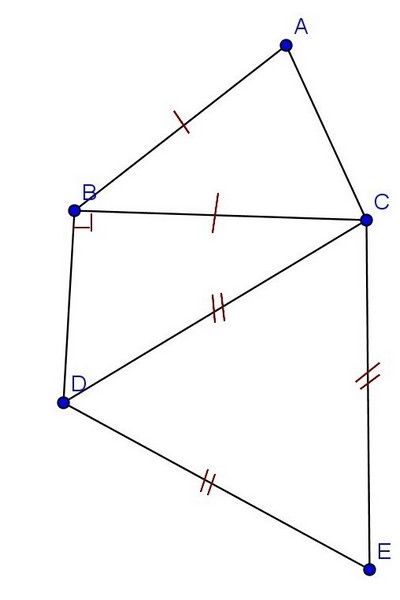
Voici une figure où les points A, B et C sont alignés .

a. Rédiger un programme de construction de cette figure .

1) Construire un segment [AC] d’une longueur de 7 cm .

2) Placer le point B sur le segment [AC] tel que AB = 3 cm.

3) Tracer les droites (d1) et (d2) perpendiculaires à (AC) passant par les points A et C.

4) Placer le point D sur la droite (d1) tel que AD = 4 cm .

5) Tracer le segment [DB] .

6) Tracer la droite (d3) perpendiculaire à [DB] passant par B.

7) Placer le point E qui est le point d’intersection des deux droites (d2) et (d3) .

Exercice 5 :

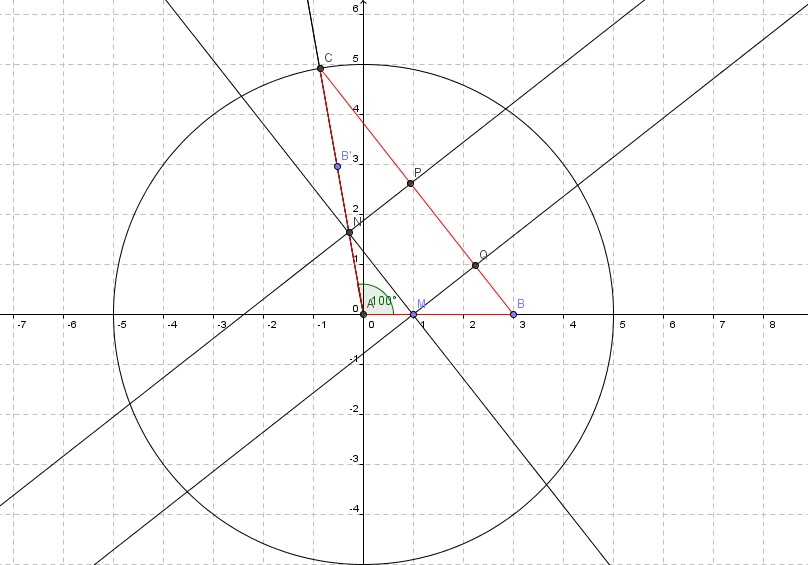
a. Tracer un triangle ABC tel que AB = 3 cm, AC = 5 cm et $\widehat{BAC}=100^{\circ}$ .

b. Placer le point M sur le segment [AB] tel que AM = 1 cm .

c. Par M, tracer la parallèle à la droite (BC); elle coupe la droite (AC) en N.

d. PAr M, tracer la perpendiculaire à la droite (BC); elle coupe (BC) en Q.

Par N, tracer la parallèle à la droite (MQ) ; elle coupe (BC) en P.

a)Voir en rouge b)c)d) voir schéma (Remarque , ne pas se soucier du point B’ qui n’était là que pour créer un angle de 100° avec le rapporteur)

e. Que peut-on dire des droites (MQ) et (MN) ?

Expliquer pourquoi .

Elle sont perpendiculaire car d’après la construction (MN) est parallèle à (BC) et que (BC) est perpendiculaire à à (MQ).

D’ailleurs toute perpendiculaire à (BC) l’est à (MN) puisque que (BC) // (MN)

// signifie « parallèle »

f. Que peut-on dire des droites (NP) et (PQ) ?

Expliquer pourquoi .

Puisque (NP) parallèle à (MQ), on sait que (PQ) est perpendiculaire à (MQ) donc perpendiculaire à (NP).

(NP) et (PQ) sont perpendiculaires

g. Quelle est la nature du quadrilatère MNPQ ?

Expliquer pourquoi .

Puisque le quadrilatère MNPQ a deux angles droit opposés, des côté parallèles. Il s’agit d’un rectangle.

Exercice 6 :

Exercice 7 :

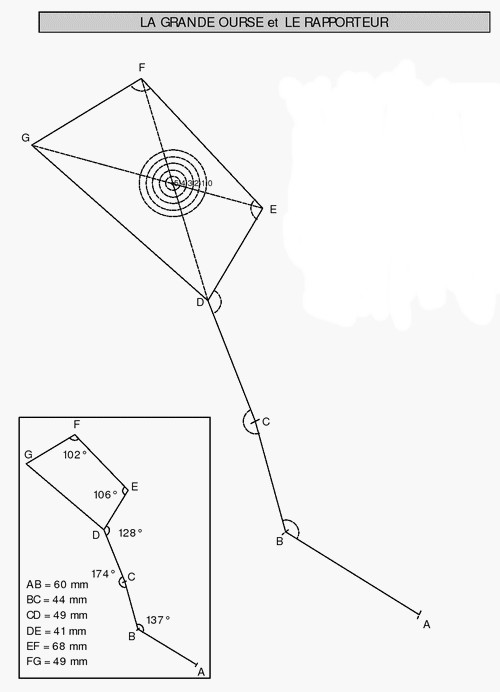
Voici quelques unes des constructions que vous devez obtenir :

Exercice 8 :

Dans chaque cas, faire la figure décrite et

indiquer la nature du triangle.

a. ABC est un triangle tel que $(AC)\perp (BC)$ .

ABC est un triangle rectangle en C .

b. MNP est un triangle tel que MN=NP et $(MN)\perp (NP)$ .

MNP est un triangle isocèle et rectangle en N .

c. EFG est un triangle isocèle en chacun de ses sommets .

EFG est un triangle équilatéral .

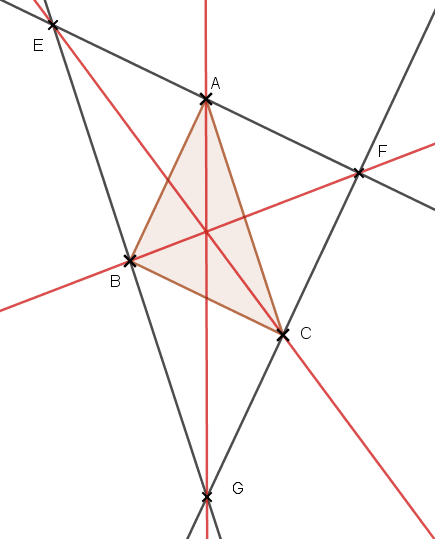
Exercice 9 :

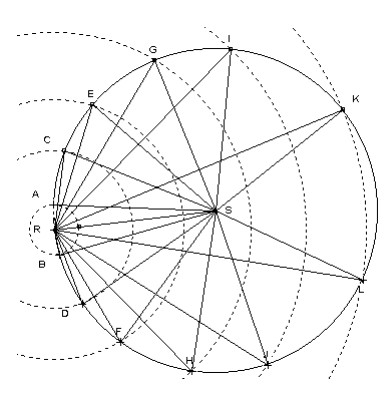
On remarque les trois droites (EC), (BF) et (AG) sont concourantes (elles se croisent les trois en un même point).

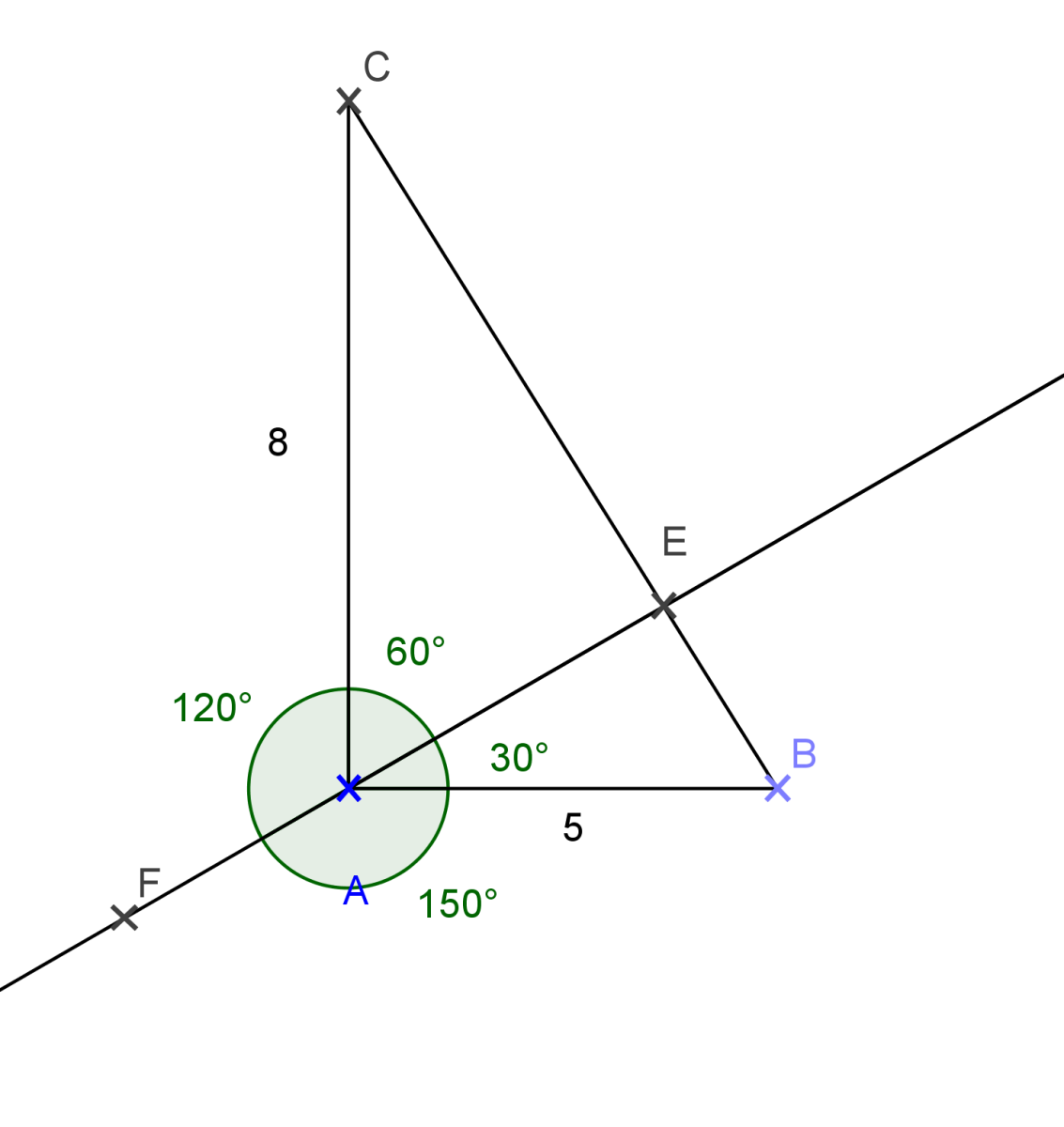
Exercice 10 :

Nous avons :

$\widehat{BCD}=30^{\circ}$

CE= 6 cm et AC = 3 cm .

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «construction de figures géométriques : corrigé des exercices en 6ème en PDF.» au format PDF.

D'autres cours et exercices à consulter

Nos applications

Téléchargez gratuitement la dernière version de nos applications.

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.