Les 4 opérations avec l’addition, la soustraction, la multiplication et la division : cours de maths en 6ème en PDF.
Mis à jour le 24 décembre 2025
I. Addition et somme de deux nombres
1.Vocabulaire et définition :
Exemple :
21 est la somme des termes 12 et 9.
L’addition a la propriété d’être commutative.
C’est-à-dire que l’on peut intervertir les différents facteurs sans en changer la valeur du produit.
Exemple :
Calculer la valeur de cette expression numérique A.
Utilisons le fait que l’addition est commutative pour calculer astucieusement cette somme.
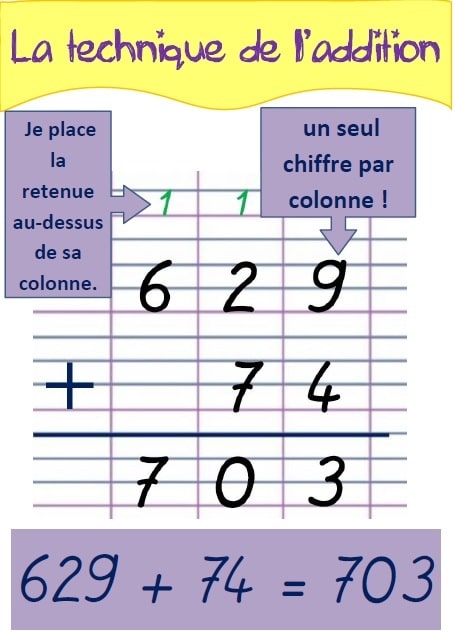
2. Poser une addition en en colonne :
Méthode :
Il faut veiller à aligner chaque position du nombre l’une au dessus de l’autre.
3.Ordre de grandeur d’une opération :
Lorsque la valeur d’une somme est compliquée à obtenir mentalement, nous fournissons un ordre de grandeur. C’est-à-dire une approximation de cette somme.
Exemple :
Donner un ordre de grandeur de la somme 
.
Nous avons 
et 
donc 
.
Un ordre de grandeur de cette somme est donc 100.
II. Soustraction de deux nombres décimaux :
1.Définition et vocabulaire :
Exemple :
11 est la différence des termes 33 et 12.
Remarques :
- Ce résultat aurait pu être trouvé en complétant une addition à trous : si
alors 
. - La soustraction n’est pas commutative, on ne peut pas modifier l’ordre des termes d’une soustraction
.
alors 
.
.2. Calcul d’une différence en colonne :
Il faut veiller à aligner chaque position du nombre l’une au dessus de l’autre.
III. Multiplication de deux nombres décimaux :
1.Définition et vocabulaire
Exemple :
75 est le produit des facteurs 15 et 5.
Remarques :
- -Lorsque l’on multiplie un nombre par 0, on obtient 0. de manière générale
. - Lorsque l’on multiplie un nombre par 1, on obtient ce nombre, de manière générale .
.
.On peut modifier l’ordre des facteurs sans que cela ne modifie la valeur du produit
.Exemple :
Cette propriété peut être utilisée pour calculer astucieusement un produit.
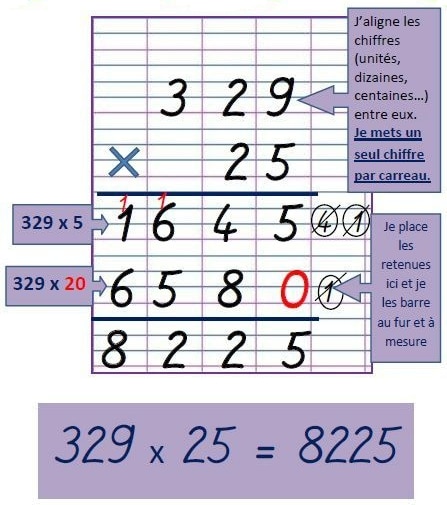
2.Calcul d’un produit en colonne :
Il faut veiller à aligner chaque position du nombre l’une au dessus de l’autre et de placer le plus grand nombre en premier afin que la multiplication contienne le moins de ligne possible.
Exemple :
Calculer le produit de 
par 
.
3.Multiplier par 10;100;1 000;0,1;0,01;0,001….
- Pour multiplier un nombre décimal par 10 ou 100 ou 1 000, il faut décaler la virgule de 1 rang ou 2 rangs ou 3 rangs vers la droite et compléter par des zéros si besoin.
- Pour multiplier un nombre décimal par 0,1 ou 0,01 ou 0,001, il faut décaler la virgule de 1 rang ou 2 rangs ou 3 rangs vers la gauche et compléter par des zéros si besoin.
Exemples :
Calculer les produits suivants :
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «les 4 opérations avec l’addition, la soustraction, la multiplication et la division : cours de maths en 6ème en PDF.» au format PDF.
Ressources de sixième
Cours de sixième
D'autres cours et exercices à consulter
🤖 Exercices IA Interactifs ✨
Des milliers d'exercices interactifs conformes aux programmes officiels. Apprenez, pratiquez et progressez à votre rythme.
Exercices interactifs
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.
