Valeur absolue et intervalle : exercices de maths en 2de corrigés en PDF.
Mis à jour le 30 septembre 2025
Exercice 1 :
Résoudre dans les équations et inéquations suivantes :
a) | 2 – x | < 4
b) | 6 – 2 x | = 3
c) | x + 2 | > 3
d) | x + 2 | < | x + 3 |
e) | x3 – 1 | + p > 0
f) 3 < | x + 2 | < 4
g) | 4 x² – 12 x + 9 | = 4
h) | 3 x + 1 | + | 1 – x | > 3
i) | 1 + x² | = 2x
Exercice 2 :
Calculer.
a) 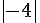 b)
b)  c)
c) 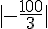
d) 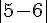 e)
e) 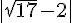 f)
f) 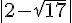
Exercice 3 :
Sans calculatrice, simplifier :
a) 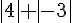 b)
b) 
c) 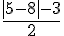 d)
d) 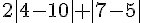
Exercice 4 :
1.a) Sur une droite graduée, placer les nombres 5 et 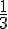 .
.
b) Calculer la distance entre 5 et 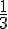 .
.
2. Reprendre la question 1. avec 3 et 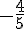 .
.
3. Reprendre la question 1. avec -1 et 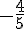 .
.
Exercice 5 :
A l’aide d’une valeur absolue, écrire la distance entre :
a) 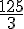 et 2. b)
et 2. b) 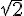 et 5
et 5
c) – 5 et 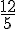 d)
d) 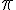 et 4
et 4
Exercice 6 :
sans calculatrice, simplifier :
a) 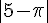 b)
b) 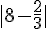 c)
c) 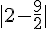
d) 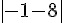 e)
e) 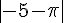 f)
f) 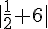
Exercice 7 :
De la même façon que 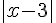 représente la distance entre le nombre réel
représente la distance entre le nombre réel  et 3,
et 3,
exprimer en termes de distance :
a) 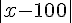 b)
b) 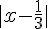
c) 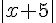 d)
d) 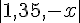
e)  f)
f) 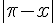
Exercice 8 :
Déterminer l’ensemble, sous la forme d’intervalle, des réels  vérifiant :
vérifiant :
a) 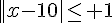 b)
b)  c)
c) 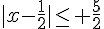
Exercice 9 :
On considère un intervalle [a ; b] avec a et b deux nombres réels.
On appelle centre de l’intervalle [a ; b] le nombre 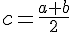
et rayon de l’intervalle [a ; b] le nombre 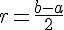 .
.
Graphiquement, on a :

1. a) Calculer le centre et le rayon de [2 ; 6].
b) Traduire |x – 4| en termes de distance entre deux réels.
c) Recopier et compléter: ![x\in[2;6]\Leftrightarrow |x-4|\leq\, ...](https://mathovore.fr/latex-images/185867f10d179ab8d2e59fe555ca8066.png)
2. De la même manière, recopier et compléter :
a) ![x\in[1;25]\Leftrightarrow |x-13|\leq\, ...](https://mathovore.fr/latex-images/bf1e8c6d00fa6c6ccbbbcba09afd7084.png) .
.
b) ![x\in[6;20]\Leftrightarrow |x-...|\leq\, ...](https://mathovore.fr/latex-images/543ce442560268d86c228f8b744f873e.png)
c) ![x\in[1,2;3]\Leftrightarrow |x-...|\leq\, ...](https://mathovore.fr/latex-images/95064cd24832f38e97607a18f375254a.png)
Exercice 10 :
Ecrire une inégalité vérifiée par  et utilisant une valeur absolue dans les cas suivants.
et utilisant une valeur absolue dans les cas suivants.
a) ![x\in [-4;5]](https://mathovore.fr/latex-images/7f79da773af20c008bb6575b486bd71d.png) b)
b) ![x\in [0;1,1]](https://mathovore.fr/latex-images/7115f0d09c631b658567033c0f3ccfd9.png) a)
a) ![x\in [ \frac{1}{3};\frac{2}{3}]](https://mathovore.fr/latex-images/54e0e97e63693c629571613d82e12a8a.png)
Exercice 11 :
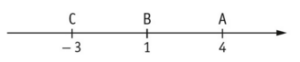
On donne un axe gradué, sur lequel on a placé les points A, B et C.
a. AB = …. b. AC = … c. BC = … d. CC = …
Exercice 12 :
On donne un axe gradué, sur lequel on a placé les points A, B et C.
Compléter les pointillés.
a. AB = …. b. AC = … c. BC = …
Exercice 13 :
Ecrire sans les barres de valeurs absolues les nombres :
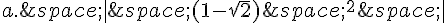
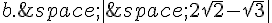
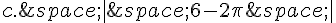

Exercice 14 :
Résoudre dans  les équations suivantes :
les équations suivantes :
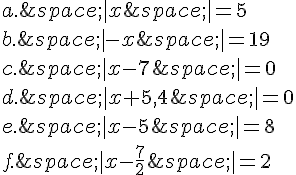
Exercice 15 :
Résoudre dans  les inéquations suivantes :
les inéquations suivantes :
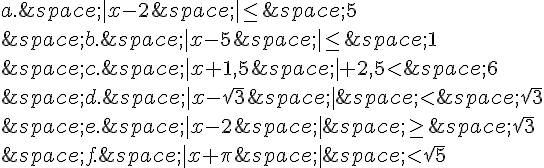
Exercice 16 :
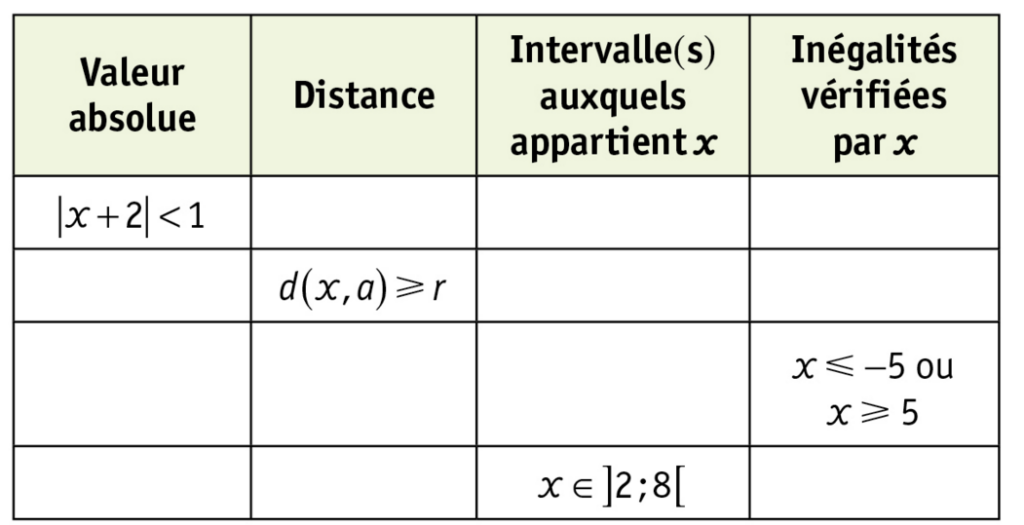
Recopier et compléter le tableau ci-dessous :
|
Enoncé |
Intervalle |
Représentation graphique |
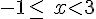 |
x 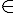 |
|
 |
x 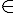 |
|
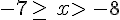 |
x 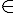 |
|
 |
x 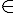 |
|
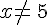 |
x 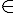 |
Exercice 17 :
Traduire sous forme d’intervalle :
1) y > – 3 et y < 4 2) y > – 3 ou y < 4
3) 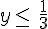 et
et 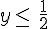 4)
4) 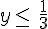 ou
ou 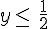
Exercice 18 :
Compléter avec les symboles 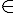 ou
ou 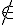 :
:
1) 7 … ] 0 ; 7 [
2) 5,9 … ] 5,8 ; +∞ [
3) – 0,25 … ] – 0,3 ; – 0,2 [ … ] 1 ; 2 ]
4) – 0,199 … ] – 0,2 ; – 0,19 [
5) 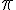 …. [ 3,14 ; 3,141 [
…. [ 3,14 ; 3,141 [
Exercice 19 :
Vrai ou faux ?
1) Si x ∈ [ 6,7 ; +∞ [ alors x ∈ [ 6 ; +∞ [.
2) Si x ∈ ] – 3 ; 4 [ alors x ∈ [ – 2 ; 5 [.
3) Si x ∉ [ – 5 ; 2[ alors x ∈ ] 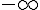 ; – 3 [ ∪ [ 2 ; +∞[.
; – 3 [ ∪ [ 2 ; +∞[.
4) L’intervalle ] 0 ; 4[ est inclus dans [ 0 ; 4 [.
5)  .
.
6) Si 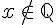 alors
alors 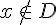 .
.
Exercice 20 :
Simplifier les notations suivantes lorsque c’est possible.
A = [ – 5 ; 7[ ∪ [ – 2 ; 12 [
B = [ 0 ; +∞ [ ∪ ] – 2 ; +∞ [
C = ] –∞ ; 0 [ ∪ [ 0 ; +∞ [
D = ] -∞ ; 4/3 [ ∩ [ – 10 ; 10 ]
E = [ – 4 ; [ ∪ ] 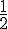 ; 10]
; 10]
Exercice 21 :
Représenter I et J sur une droite graduée, puis déterminer I ∩ J et I ∪ J.
1) I = [ 2 ; 5,5 ] et J = ] 1 ; 3 ].
2) I = [ – 1 ; +∞ [ et J = ] –2 ; 3 ].
3) I = ] – 1 ; 3 ] et J = [ – 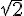 ;
; 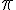 [.
[.
4) 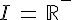 et
et 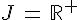 .
.
5) I = {1 ; 2 ; 3 ; 4} et J = [ – 5 ; 5 ].
Exercice 22 :
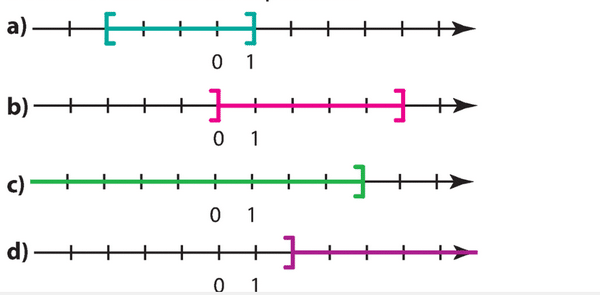
On considère des droites graduées sur lesquelles on a marqué des ensembles de nombres.
Donner l’intervalle correspondant.
Exercice 23 :
Représenter sur une droite graduée et décrire, à l’aide d’un intervalle, chacun des ensembles de nombres réels  tels que :
tels que :
a) 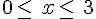 b)
b) 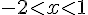
c) 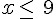 d)
d) 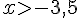
Exercice 24 :
Représenter sur une droite graduée chacun des intervalles suivants.
a) ![]1,6]](https://mathovore.fr/latex-images/11b62dd4ad59f658fdddb77cf0f7419a.png) b)
b) ![[-0,5;3,2]](https://mathovore.fr/latex-images/aa6fcd2ba348516ae2ea758a5f16af8c.png)
c) ![]-\infty;2]](https://mathovore.fr/latex-images/0e4e6ce2cdd38eb979c53a699dca169c.png) d)
d) 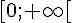
Exercice 25 :
Ecrire les inégalités vérifiées par les réels  pour chacun des cas suivants.
pour chacun des cas suivants.
a) ![x\in[0;1,2]](https://mathovore.fr/latex-images/7afe475ccb875ac3f0b02821d6596437.png) b)
b) ![x\in]-\frac{5}{3};3]](https://mathovore.fr/latex-images/07ae91a5223917d2ca7c1bedb73347d4.png)
c) 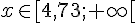 d)
d) ![x\in\,]-\infty;0[](https://mathovore.fr/latex-images/aff967dee5d46cbb5121faaca470eae2.png)
Exercice 26 :
Recopier et compléter par les signes 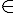 et
et 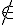 .
.
a) ![1,4...[0;7]](https://mathovore.fr/latex-images/ee7feef25e55c7ffe5cd7e0cc2db22a9.png) b)
b) ![-\pi...]-3;-1[](https://mathovore.fr/latex-images/a2e278bf7dcf9632909acd8d7ac02013.png)
c) 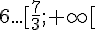 d)
d) ![-3...\,]-\infty;-3,5[](https://mathovore.fr/latex-images/36e0eb973a8579c4f3da1a38b54539fc.png)
Exercice 27 :
Sans calculatrice, dire si 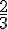 appartient aux intervalles suivants.
appartient aux intervalles suivants.
a) ![[0;\frac{4}{5}]](https://mathovore.fr/latex-images/9a670f97c3760a120c5b1edf9233c560.png) b)
b) ![[\frac{3}{5};1]](https://mathovore.fr/latex-images/2ef9bb913ef4a052c4d1e545cecded2e.png) c)
c) ![[\frac{1}{3};\frac{2}{5}]](https://mathovore.fr/latex-images/ecc15a5a4f2bd705a65227714a71002a.png)
Exercice 28 :
Soit ![I=[-6;8]](https://mathovore.fr/latex-images/e854f90a89002aa83cf96ce9b2199ffb.png) et
et ![J=]2;100[](https://mathovore.fr/latex-images/4988dd289cba61874d0dcb0eae96b5e6.png) .
.
Dire si chacun des nombres suivants appartient à I, à J, à 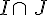 , à
, à 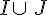 .
.
a) – 10 b) – 6 c) – 0,5 d) 2
e) 8,1 f) 99,9 g) 1 000 h) 0
Exercice 29 :
Compléter le tableau suivant :
Exercice 30 :
Parmi les affirmations suivantes, lesquelles sont vraies ?
Justifier.
a. Quels que soient les réels a et b, 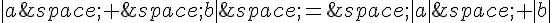 .
.
b. Si  alors x=0.
alors x=0.
c. 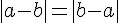
d. 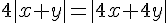 .
.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «valeur absolue et intervalle : exercices de maths en 2de corrigés en PDF.» au format PDF.
Ressources de seconde
Cours de seconde
D'autres cours et exercices à consulter
🤖 Exercices IA Interactifs ✨

Des milliers d'exercices interactifs conformes aux programmes officiels. Apprenez, pratiquez et progressez à votre rythme.
Exercices interactifsL'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.