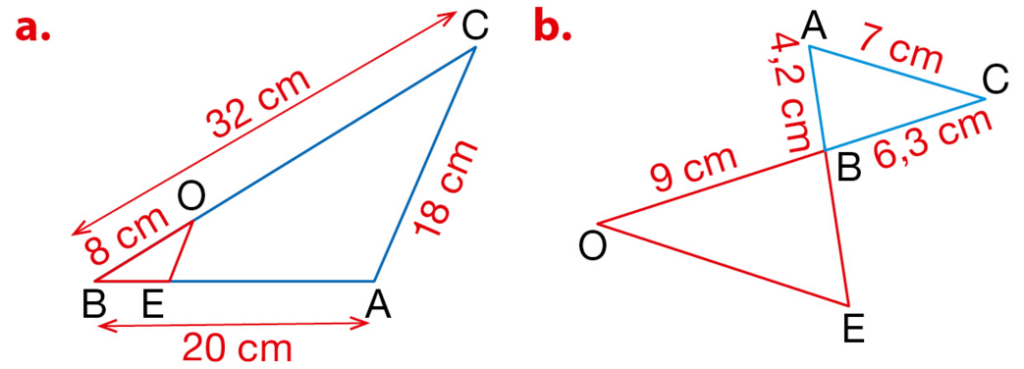
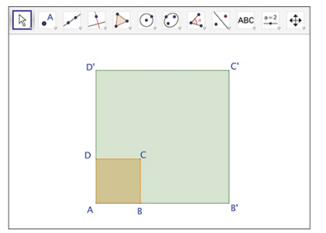
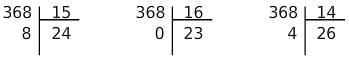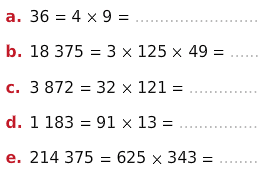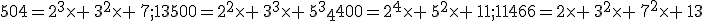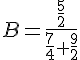Exercice 1 : divisions euclidiennes.
Les trois divisions euclidiennes ci-dessous sont exactes.
- Les nombres 14,15 et 16 sont-ils des diviseurs de 368?Justifier.
- Quel est le plus petit multiple de 15 supérieur à 368?Justifier.
- Quel est le plus grand multiple de 14 inférieur à 368 ?Justifier.
Exercice 2 : dividende, diviseur, quotient et reste.
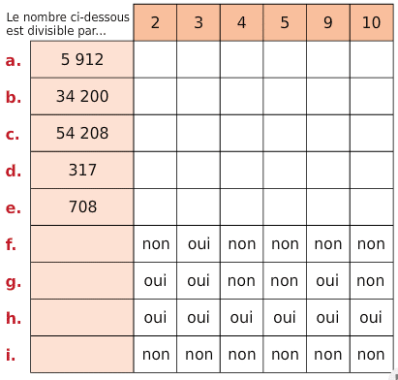
Compléter le tableau suivant, sans poser les divisions, puis écrire les égalités euclidiennes correspondantes.
Exercice 3 : problème du centre aéré.
Un centre aéré accueillant 131 enfants organise une journée « Sport Co » avec du basket, du hand-ball, du football et du rugby.
Pour chaque sport, combien peut-on constituer d’équipes?
Combien d’enfants seront sans équipe ?
Exercice 4 : liste des diviseurs
Ecrire la liste des diviseurs des nombres suivants : 16; 20; 36; 90; 59; 33.
Exercice 5 : critères de divisibilité.
Compléter le tableau ci-dessous.
Exercice 6 : démonstration.
Démontrer que la somme de deux entiers positifs consécutifs et impairs est un multiple de 4.
Démontrer qu’un multiple de 8 est également un multiple de 4.
Exercice 7 : des paquets de billes.

Le contenu de chaque paquet doit être identique.
Combien de paquets pourra-t-il réaliser?
Trouver les différentes possibilités.
- Peut-il y avoir 9 paquets? 30 paquets?
- Donner la liste des diviseurs de 90 puis de 150.
- Quelles sont les différentes possibilités pour le nombre de paquets ?
Exercice 8 : liste des nombres premiers.
Donner la liste de tous les nombres premiers inférieurs à 50.
Exercice 9 : décomposition en facteurs premiers.
Utiliser les égalités ci-dessous pour écrire les décompositions en facteurs premiers
des nombres proposés.
Exercice 10 : écrire la décomposition en facteurs premiers.
Ecrire la décomposition en facteurs premiers des nombres entiers suivants :
180; 63; 1 225; 3 672; 416; 24 000.
Exercice 11 : trouver un entier.
Trouver le nombre recherché.
Exercice 12 : fractions irréductibles.
Utiliser les décompositions en facteurs premiers pour rendre ces fractions irréductibles.
rendre irréductibles les fractions suivantes :.
Exercice 13 : simplifier des fractions.
Rendre irréductible les fractions suivantes : .
Exercice 14 : problème des CD.
je possède plus de 400 cd mais moins de 450. Que je les groupe par 2, par 3 , par 4 ou par 5, c’est toujours la même chose: il en reste un tout seul.
Combien Nori a-t-il de cd ?
Exercice 15 :
1. Calculer le PGCD de 110 et de 88.
2. Un ouvrier dispose de plaques de métal de 110 cm de longueur et de 88 cm de largeur.
Il a reçu la consigne suivante :
« Découper dans ces plaques des carrés, tous identiques, les plus grands possibles,
de façon à ne pas avoir de perte. »
Quelle sera la longueur du côté du carré ?
3. Combien obtiendra-t-on de carrés par plaque ?
Exercice 16 :
1. Calculer le PGCD de 114 400 et 60 775.
2. Expliquer comment, sans utiliser la touche « fraction » d’une calculatrice, rendre irréductible la fraction
.
3. Donner l’écriture simplifiée de
.
Exercice 17 :
Soient les nombres A = et B = –
.
1. Expliquer pourquoi la fraction A n’est pas irréductible.
2. Simplifier cette fraction pour la rendre irréductible.
3. Montrer, en indiquant les étapes de calcul, que A – B est un nombre entier.
Exercice 18:
1. Démontrer que les nombres 65 et 42 sont premiers entre eux.
2. Démontrer que =
.
Exercice 19 :
1. Déterminer le PGCD de 108 et 135.
2. Marc a 108 billes rouges et 135 billes noires.
Il veut faire des paquets de sorte que :
- tous les paquets contiennent le même nombre de billes rouges ;
- tous les paquets contiennent le même nombre de billes noires ;
- toutes les billes rouges et les billes noires soient utilisées.
a. Quel nombre maximal de paquets pourra-t-il réaliser ?
b. Combien y aura-t-il alors de billes rouges et de billes noires dans chaque paquet ?
Exercice 20 :
1. Calculer le PGCD de 1 756 et 1 317 (on détaillera les calculs nécessaires).
2. Un fleuriste a reçu 1 756 roses blanches et 1 317 roses rouges.
Il désire réaliser des bouquets identiques
(c’est à dire comprenant un même nombre de roses et la même
répartition entre les roses blanches et les rouges) en utilisant toutes les fleurs.
a. Quel sera le nombre maximum de bouquets identiques ? Justifier clairement la réponse.
b. Quel sera alors la composition de chaque bouquet ?
Exercice 21 :
Rendre les fractions suivantes irréductibles en calculant le PGCD de leurs numérateurs et leurs dénominateurs.
et
Exercice 22 :
1. Déterminer par la méthode de votre choix et en détaillant les différentes étapes le PGCD de 144 et 252.
2. Une association organise une compétition sportive; 144 filles et 252 garçons se sont inscrits.
L’association désire répartir les inscrits en équipes mixtes.
Le nombre de filles doit être le même dans chaque équipe, ainsi que le nombre de garçons.
Tous les inscrits doivent être dans une des équipes.
a. Quelle le nombre maximal d’équipes que cette association peut former ?
b. Quelle est alors la composition de chaque équipe ?
Exercice 23 :
1. Les nombres 682 et 352 sont-ils premiers entre eux ? Justifier.
2. Calculer le plus grand diviseur commun (PGCD) de 682 et 352.
3. Rendre irréductible la fraction
en indiquant clairement la méthode utilisée.
Exercice 24 :
Calculer et donner le résultat sous forme d’une fraction irréductible :
.
Exercice 25 :
Calculer et donner le résultat en notation scientifique :
Exercice 26 :
1. On donne :
.
Calculer A et donner le résultat sous la forme d’une fraction .
2. On donne .
Ecrire B sous la forme où b est un nombre entier .
3. On donne
Calculer C et donner l’écriture scientifique du résultat .
Exercice 26 :
Calculer et mettre sous la forme la plus simple possible :
.
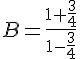
.
.
Exercice 27 :
1. Déterminer le pgcd de 288 et 224.
2. Écrire la fraction sous forme irréductible.
3. Un photographe doit réaliser une exposition en présentant ses oeuvres sur des panneaux contenant chacun le même nombre de photos de paysage et le même nombre de portraits.
Il dispose de 224 photos de paysage et de 288 portraits.
a) Combien peut-il réaliser au maximum de panneaux en utilisant toutes les photos ?
b) Combien chaque panneau contient-il de photos de paysage et de photos de portraits ?
Exercice 28 : création de bijoux.
Louise, créatrice de bijoux, a acheté un lot de perles jaunes, vertes et bleues.
Elle souhaite fixer ces perles à un modèle de bracelet qu’elle a créé.
Elle désire utiliser toutes les perles de façon a réaliser un nombre maximum de bracelets identiques.
Aider Louise à déterminer le nombre de perles de chaque couleur que comportera un bracelet ainsi que le prix de vente minimal d’un bracelet .
sachant que pour la vente de ces bracelets soit rentable, les coûts de fabrication (y compris de l’achat de perles) ne doivent pas représenter plus de deux septièmes du prix de vente.
138 perles jaunes pour 55.20€
184 perles vertes pour 64.40€
230 perles bleues pour 78.20€
coût de la chaine pour un bracelet : 1.50€
coût du fermoir pour un bracelet : 2.40€
main d’oeuvre : 20€ pour 8 bracelets.
Exercice 29 :
Vous êtes libre d’utiliser la méthode que vous préférez.
a. 255 et 154 sont-ils premiers entre eux ?
b. 609 et 465 sont-ils premiers entre eux ?
c. 11 913 et 7 259 sont-ils premiers entre eux ?
Exercice 30 :
1. Calculer le pgcd de 481 et 234 .
2. Ces deux entiers sont-il premiers entre eux?
Exercice 31 :
1. Calculer le pgcd de 137 et 41 par la méthode de l’algorithme d’Euclide.
2. Ces deux entiers sont-ils premiers entre eux?
Exercice 32 :
Un chocolatier vient de fabriquer 2 622 œufs de Pâques et 2 530 poissons en chocolat.
Il souhaite vendre des assortiments d’œufs et de poissons de façon que :
• tous les paquets aient la même composition.
• après mise en paquet, il reste ni œufs, ni poissons.
1. Aider ce chocolatier à choisir la composition de chaque paquet : donner toutes les possibilités.
2. Quel est le plus grand nombre de paquets qu’il peut réaliser ?
Exercice 33 :
On répartit en paquets un lot de 161 crayons rouges et un lot de 133 crayons noirs de façon que tous les crayons d’un paquet soient de la même couleur et que tous les paquets contiennent le même nombre de crayons.
1. Combien y a-t-il de crayons dans chaque paquet ?
2. Quel est le nombre de paquets de crayons de chaque couleur ?
Exercice 34 :
Simplifier les fractions suivantes jusqu’à obtenir la fraction irréductible.
Exercice 35 :
Calculer et écrire sous la forme d’une fraction irréductible
Exercice 36 :
1. Déterminer le PGCD de 108 et 135.
2. Marc a 108 billes rouges et 135 billes noires.
Il veut faire des paquets de sorte que :
– tous les paquets contiennent le même nombre de billes rouges ;
– tous les paquets contiennent le même nombre de billes noires ;
– toutes les billes rouges et les billes noires soient utilisées.
a. Quel nombre maximal de paquets pourra-t-il réaliser ?
b. Combien y aura-t-il alors de billes rouges et de billes noires dans chaque paquet ?
Exercice 37 :
En allant au collège, Samy dit à Daniel :
« J’ai plus de 400 CD, mais moins de 450. En les regroupant par 2, ou par 3, ou par 4, ou par 5, c’est toujours la même chose, il en reste un tout seul ».
Combien de CD, Samy possède-t-il ?
Exercice 38 :
a) A la question : « Combien 48 a-t-il de diviseurs ? », Jean répond qu’il y en a 9, alors que Cédric, lui, en trouve 10.
Qui a raison ?
Quelle méthode permet de trouver tous les diviseurs d’un nombre ?
b) Un artiste dispose d’une toile de 60 cm sur 48 cm.
Il veut y peindre un pavage composé de carrés identiques, mais de couleurs différentes. La longueur du côté de ces carrés est un nombre entier.
Quelle est la plus grande longueur possible pour ces carrés ( en cm ) ?
Exercice 39 :
Les phrases suivantes sont-elles vraies ou fausses ? Justifier les réponses.
a) 3 est un diviseur de 43. g) 24 a pour multiple 240.
b) 132 est divisible par 11. h) 5 divise 450.
c) 7 a pour diviseur 21. i) 8 est un diviseur de 0.
d) 222 est un diviseur de 31 024. j) 1 est un multiple de 67.
e) 31 024 est un multiple de 113. k) 1 divise 0.
f) 45 a pour diviseur 5. l) 0 divise 15.
Exercice 40 :
Quelle que soit la valeur du nombre entier n, le nombre , n’a que 2 diviseurs.
Vrai ou faux ?
La solution devra être présentée dans une feuille de calcul d’un tableau avec les explications nécessaires.
Exercice 41 :
Un pâtissier dispose de 411 framboises et de 685 fraises.
Afin de préparer des tartelettes, il désire répartir ces fruits en les utilisant tous
et en obtenant le maximum de tartelettes identiques .
. Calculer le nombre de tartelettes .
2. Calculer le nombre de framboises et de fraises dans chaque tartelette .
Exercice 42 :
Un fleuriste a reçu 1 105 oeillets et 935 iris.
Il souhaite confectionner un nombre maximal de bouquets de la manière suivante :
– chaque bouquet doit avoir le même nombre d’iris ;
– chaque bouquet doit avoir le même nombre d’oeillets ;
– tous les oeillets et tous les iris doivent être utilisés .
1. Combien de bouquets le fleuriste pourra-t-il constituer ?
2. Quelle sera la constitution de chaque bouquet ?
Exercice 43 :
1) Les nombres 3120 et 2760 sont premiers entre eux ? Justifier
2) Calculer le plus grand diviseur commun de 3120 et 2760.
3) Rendre irréductible la fraction .
4) Un confiseur dispose de 3120 dragées roses et de 2760 dragées blancs, il souhaite faire des paquets tous identiques de dragées roses et blancs.
Afin de faire un bénéfice maximum sur ces ventes, le nombre de paquets doit être le plus grand possible et il doit utiliser tous ses dragées.
a) Quel est le nombre de paquet que le confiseur confectionne ?
b) Quel est le nombre dans chaque paquet de dragées roses ?
c) Quel est le nombre dans chaque paquets de dragées blancs ?
Exercice 44 :
Écrire sous forme de fraction irréductible le nombre .
Indication : on pourra donner la décomposition en facteurs premiers des nombres 325 et 1 053 puis calculer le PGCD des nombres 1 053 et 325.
Exercice 45 :
1.Donner la décomposition en facteurs premiers des nombres 630 et 924.
2.Ecrire sous forme irréductible la fraction en donnant le détail de tous les calculs.
Exercice 46 :
Un philatéliste possède 1 631 timbres français et 932 timbres étrangers. Il souhaite vendre toute sa collection en réalisant des lots identiques, c’est à dire comportant le même nombre de timbres et la même répartition de timbres français et étrangers
1. Calculer le nombre maximum de lots qu’il pourra réaliser.
2. Combien y aura-t-il, dans ce cas, de timbres français et étrangers par lot ?
Exercice 47 :
1/ Déterminer le PGCD des nombres 108 et 135.
2/ Marc à 108 billes rouges et 135 noires. Il veut faire des paquets de sorte que :
– Tous les paquets contiennent le même nombre de billes rouges ;
– Tous les paquets contiennent le même nombre de billes noires ;
– Toutes les billes rouges et toutes les billes noires sont utilisées.
a. Quel nombre maximal de paquets pourra-il réaliser ?
b. Combien y aura-t-il de billes rouges et de billes noires dans chaque paquet ?
Exercice 48 :
1.Donner la décomposition en facteurs premiers des nombres 325 et 1053.
2.Écrire sous forme de fraction irréductible le nombre
Exercice 49 :
1.Déterminer la décomposition en facteurs premiers de 110 et 88.
2.Calculer le PGCD de 110 et 88.
3.Un ouvrier dispose de plaques de métal de 110 cm de longueur et de 88 cm de largeur. Il a reçu la consigne suivante : « Découper dans ces plaques des carrés tous identiques, les plus grands possibles, de façon à ne pas avoir de perte ».
Quelle sera la longueur du côté d’un carré ?
4.Combien obtiendra-t-il de carrés par plaques ?
Exercice 50 :
Pour le 1er Mai, Julie dispose de 182 brins de muguet et 78 roses.
Elle veut faire le plus grand nombre de bouquets identiques en utilisant toutes les fleurs.
Combien de bouquets identiques pourra-t-elle faire ?
Quelle sera la composition de chaque bouquet ?
Exercice 51 :
Un chocolatier vient de fabriquer 2 622 œufs de Pâques et 2 530 poissons en chocolat.
Il souhaite vendre des assortiments d’œufs et de poissons de façon que :
® tous les paquets aient la même composition.
® après mise en paquet, il reste ni œufs, ni poissons.
1) Aider ce chocolatier à choisir la composition de chaque paquet : donner toutes les possibilités.
2) Quel est le plus nombre de paquets qu’il peut réaliser ?
Exercice 52 :
On répartit en paquets un lot de 161 crayons rouges et un lot de 133 crayons noirs de façon que tous les crayons d’un paquet soient de la même couleur et que tous les paquets contiennent le même nombre de crayons.
a) Combien y a-t-il de crayons dans chaque paquet ?
b) Quel est le nombre de paquets de crayons de chaque couleur ?
Exercice 53 :
Une boite de jeux de société a la forme d’un parallélépipède rectangle. Les arêtes mesurent un nombre entier de centimètres ; les faces ont pour aire 96 cm², 160 cm² et 240 cm².
Quel est le volume de la boite ?
Exercice 54 :
Une malle a la forme d’un parallélépipède rectangle de dimensions 140 cm, 112 cm et 84 cm. On veut la remplir de cubes identiques dont l’arête mesure un nombre entier de centimètres.
1) Calculer l’arête du plus grand cube possible.
2) Calculer les arêtes des autres cubes qui pourraient remplir la malle.
3) Calculer dans chaque cas le nombre de cubes nécessaires pour remplir la malle.
Exercice 55 :
Les côtés d’un terrain triangulaire mesurent 198 m, 254 m et 306 m.
On plante des arbres le long des côtés, également espacés, avec un arbre à chaque sommet. La distance qui sépare deux arbres consécutifs est mesurée par un nombre entier de mètres.
Quel le nombre minimum d’arbres qu’il faut acheter ?
Exercice 56 :
Deux bus A et B partent en même temps du terminus 7 h.
Le bus A part toutes les 36 min du terminus alors que le bus B part toutes les 24 min.
A quelle heure les deux bus partiront de nouveau en même temps :
a. pour la première fois ?
b. pour la deuxième fois ?
c. pour la cinquième fois ?
Exercice 57 :
Dans la liste suivante, un seul nombre est un nombre premier. Lequel ?
Exercice 58 :
Alan possède un nombre premier de macarons.
Pourra-t-il les partager avec ses amis de manière équitable ?
Expliquer.
Exercice 59 :
Patricia place ses 24 pions sur une grille de façon à former le plus grand nombre de rectangles
de dimensions différentes.
En voici un exemple. On compte ces deux rangements comme une seule possibilité.
a. Trouver toutes les possibilités de Patricia pour placer ainsi ses 24 pions.
b. Léo affirme : « Avec le nombre de pions que je possède, je n’ai qu’une possibilité. »
Que peut-on en déduire pour le nombre de pions de Léo ?
Exercice 60 :
Nadia a remarqué que 256 = 16 x 16.
A l’aide de cette remarque, écrire la décomposition en produit de facteurs premiers du nombre 256.
Exercice 61 :
Une boîte contient 150 bonbons au chocolat noir et 120 au chocolat blanc.
a. Donner sous forme d’une fraction irréductible la proportion de bonbons au
chocolat noir dans la botte.
b. Hugo mange 3 bonbons au chocolat noir et 3 bonbons au chocolat blanc.
A-t-on encore la même proportion de bonbons au chocolat noir dans la boîte ?
Exercice 62 :
Grâce un algorithme trouvé sur Internet, Paul a obtenu les résultats suivants :
•
•
Lors d’un match de rugby, le stade comptait 59 535 spectateurs dont 33 291 supporters de l’équipe
française.
Donner la fraction irréductible représentant la proportion de supporters de l’équipe française.
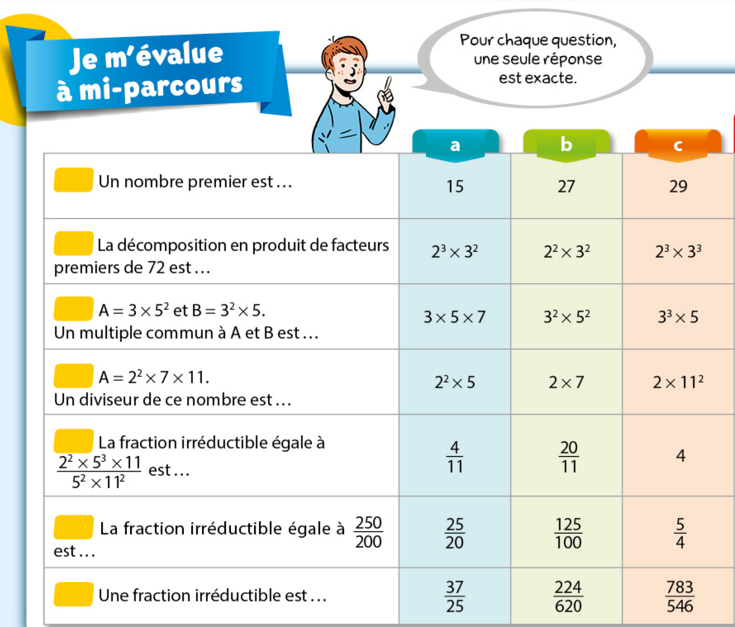
Exercice 63 :
Effectuer le QCM sur l’arithmétique et la décomposition en facteurs premiers suivant :