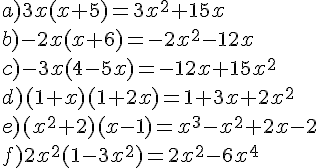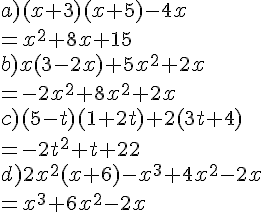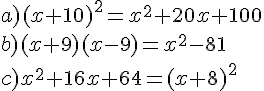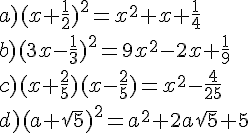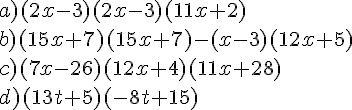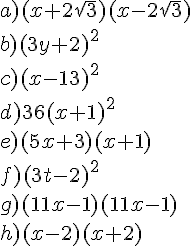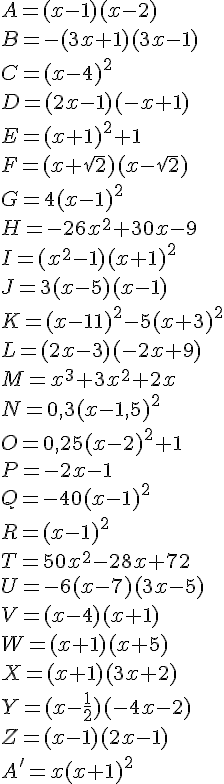EXERCICE 1 :
a)
b)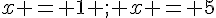
c) 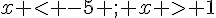
d) 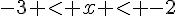
e)
f) 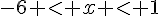

g) 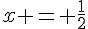

h) 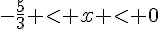
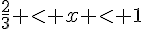
i) 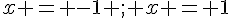
EXERCICE 2 :
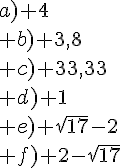
EXERCICE 3 :
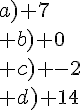
EXERCICE 4 :
1.a) A effectuer.
b) La distance entre 5 et 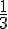
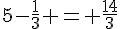
2. A effectuer.
La distance entre 3 et 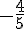
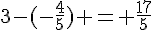
3. A effectuer
La distance entre – 1 et 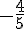

EXERCICE 5 :
a) 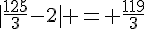
b) 
c) 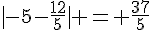
d) 
EXERCICE 6 :
a) 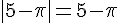
b) 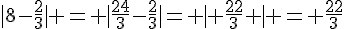
c) 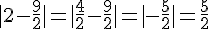
d)
e)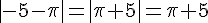
f) 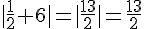
EXERCICE 7 :
a) 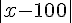
b) 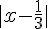
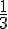
c) 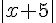
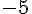
d) 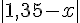


e) 


f) 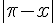

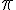
EXERCICE 8 :
a) L’inégalité 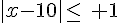
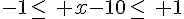
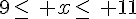
Donc l’ensemble des réels x vérifiant cette inégalité est [9 ; 11].
b) L’inégalité 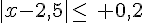
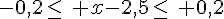
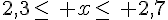
c) L’inégalité 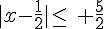
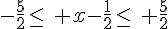
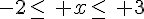
Donc l’ensemble des réels x vérifiant cette inégalité est [-2 ; 3].
EXERCICE 9 :

1. a) Le centre de [2 ; 6] est 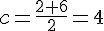
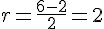
b) |x – 4| représente la distance entre x et 4 sur la droite des réels.
c) ![x\in[2;6]\Leftrightarrow |x-4|\leq\,\,\, 2](https://mathovore.fr/latex-images/e4d66ec967117db39d8b8f24cc140b92.png)
2. a) Le centre de [1 ; 25] est 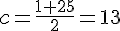

b) Le centre de [6 ; 20] est 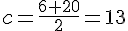
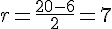
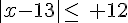
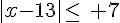
c) Le centre de [1,2 ; 3] est 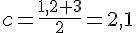

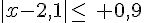
EXERCICE 10 :
a) 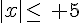
b) 
c) 
Exercice 16 :
Enoncé
Intervalle
Représentation graphique
![-1\leq\,\,\,\,x<3 ;x \in [-1, 3[\ 4>x>0 x \in ]0, 4[\ -7\geq\,\,\,\,x>\,-8 ;x \in ]-\infty, -8] \cup (-7, \infty[\ x\in\,\mathbb{R}^+; x \in ]0, \infty[\ x\neq\,5; x \in \mathbb{R} \backslash \{5\}\](https://mathovore.fr/latex-images/1f6a5f720b505ac2c43f056fa6a628c0.png)
Exercice 17 :
1) 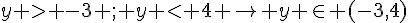
2) ![y > - 3\, ou\, y < 4 \to y \in ]-\infty,-3[\cup ]-3,4[ \cup ]4, \infty[](https://mathovore.fr/latex-images/692a4bd584e1d220e0ffeae9e13b0bd9.png)
3) ![y\leq\,\,\,\,\frac{1}{3} et y\leq\,\,\,\,\frac{1}{2} \to y \in ] -\infty, \frac{1}{3} ]](https://mathovore.fr/latex-images/5be9147a7a20187180ec4df55739a4ca.png)
4) ![y\leq\,\,\,\,\frac{1}{3} ou y\leq\,\,\,\,\frac{1}{2} \to y \in ]-\infty, \frac{1}{2}]](https://mathovore.fr/latex-images/745a5c934cd5e7b4d8af8b6258c48329.png)
Exercice 18 :
1) ![7... ] 0 ; 7 [ \to 7 \notin ]0,7[](https://mathovore.fr/latex-images/91b15b2bf1983cd0b26b3a3382daa2b1.png)
2) ![5,9... ] 5,8 ;+\infty[ \to 5,9 \in ]5,8, +\infty[](https://mathovore.fr/latex-images/10c16fb2b44a4fd296030e5a73a1f499.png)
3) ![-0,25 ... ]- 0,3 ; - 0,2 [ ... ] 1 ; 2 ] \to -0,25 \in [-0,3,-0,2] \notin ]1,2[](https://mathovore.fr/latex-images/615f5782deecd6295ba124eec2cd2433.png)
4) ![- 0,199... ] - 0,2 ; - 0,19 [ \to -0,199 \in ]-0,2,-0,19[](https://mathovore.fr/latex-images/8aa765709a1d452eb9edd702af712d98.png)
5) 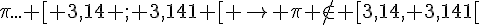
Exercice 19 :
1) Vrai
2) Vrai
3) Faux
4) Vrai
5) Vrai
6) Faux
Exercice 20 :
A = [ – 5 ; 12 [
B = ] –∞ ; +∞ [
C = ] –∞ ; +∞ [
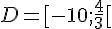
![E = ] -\infty ; -4 ] \cup ] \frac{1}{2} ; 10]](https://mathovore.fr/latex-images/374c9bd6d39c0757cb21558afb4ace9f.png)
Exercice 21 :
1)
I ∩ J = ] 2 ; 3 ] ; I ∪ J = [ 1 ; 5,5 ]
2)
I ∩ J = ] – 1 ; 3 [ ; I ∪ J = [ – 1 ; +∞ ]
3)
I ∩ J = ![] - 1 ; \pi [](https://mathovore.fr/latex-images/14bf6489ad0646a00b47d4826781a93c.png)
![]-\sqrt{2}; \pi [](https://mathovore.fr/latex-images/e2549dee76479e9932ac40d7cae8137e.png)
4)
I ∩ J = Ø ; I ∪ J = 
5)
I ∩ J = Ø ; I ∪ J = [ – 5 ; 5 ]
Exercice 22 :
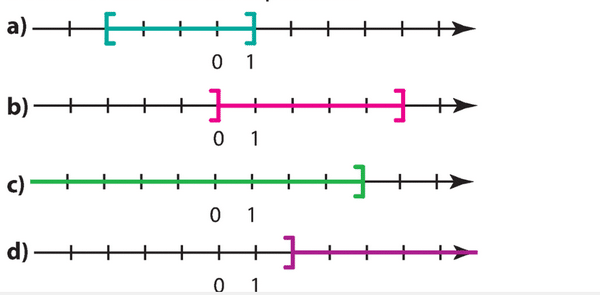
Exercice 23 :
a) [0 ; 3]
b) ]-2 ; 1[
![c) ]-\infty ; 9]](https://mathovore.fr/latex-images/59f77f679ab88d1b050d11d8a5eb8bfc.png)
![d) ]-3,5 ; +\infty[](https://mathovore.fr/latex-images/e153137e81acf5bac2e12a32482f4dd4.png)
Exercice 24 :
a) ]1 ; 6]
b) [–0,5 ; 3,2]
![c) ]-\infty ; 2]](https://mathovore.fr/latex-images/79227d807bdaf7a85f5ffc2eddd4cfed.png)
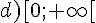
Exercice 25 :
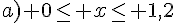
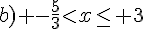
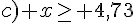
d) x<0
Exercice 26 :
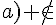
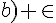
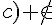
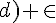
Exercice 27 :
a) Non
b) Non
c) Oui
Exercice 28 :
a) Non
b) Oui
c) Non
d) Non
e) Non
f) Oui
g) Non
h) Oui