Aires et périmètres : exercices de maths en 6ème corrigés en PDF.

Mis à jour le 29 juin 2025

---

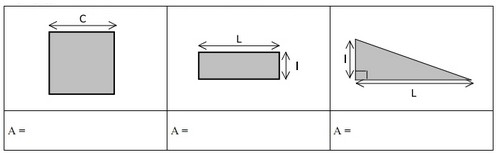
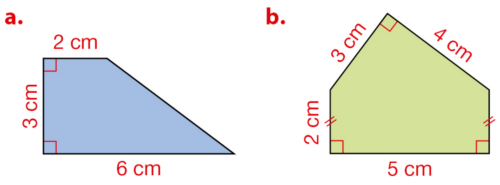
Exercice 1 – Formules des aires d’une figure géométrique

Donner les formules permettant de calculer l’aire A des figures suivantes :

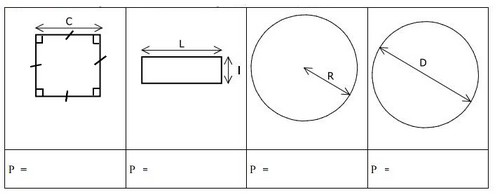
Exercice 2 – Formules des périmètres des figures

Donner les formules permettant de calculer le périmètre P des figures géométriques suivantes :

Exercice 3 – Conversion de grandeurs

Effectuer les conversions suivantes :

8 km en m .

7,5 m en mm

98,2 hm en dm

2 m en km

3 000 cm en km

650 000 cm en hm

0,05 km en  m

7,25 km en cm

7 mm en hm

20 m en dam

Exercice 4 – Calcul de périmètre

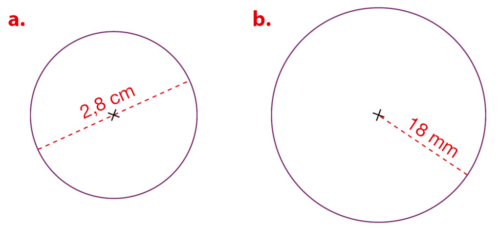
Exercice 5 :

Dans chaque cas, calculer une valeur approchée au dixième près de la longueur, en cm, de chaque
cercle.

Exercice 6 :

Calculer l’aire, en cm², de la figure (donner éventuellement une valeur approchée au centième près).

Exercice 7 :

Dans chaque cas, sans calcul ni mesure, comparer les périmètres des deux figures vertes.

Exercice 8 :

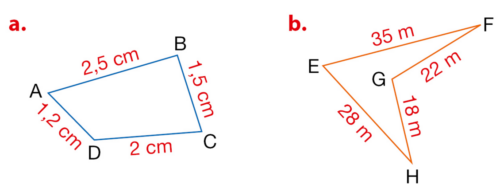
Calculer le périmètre de chaque polygone représenté.

Exercice 9 :

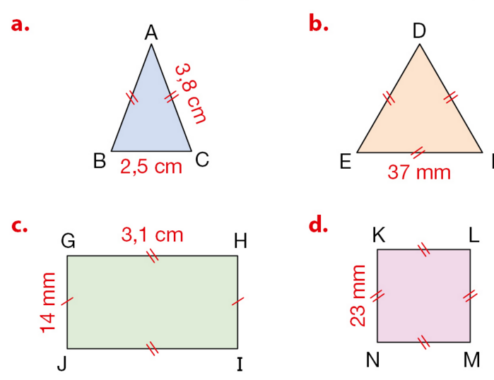
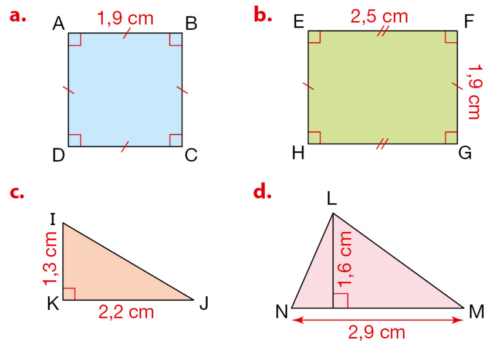
Calculer le périmètre de chacune des figures suivantes en tenant compte des dimensions indiquées.

Exercice 10 :

Columbus Circle est une place circulaire de New York au centre de laquelle s’élève une statue
de Christophe Colomb.

Le cercle intérieur a un diamètre de 64 m et le cercle extérieur a un rayon de 66 m.

Calculer une valeur approchée au centième près de la longueur, en m, de chacun de ces cercles.

Exercice 11 :

Calculer l’aire de chaque figure.

Exercice 12 :

Calculer l’aire de chaque surface colorée représentée ci-dessous.

Exercice 13 :

Calculer l’aire, en dm², de la surface colorée représentée ci-dessous.

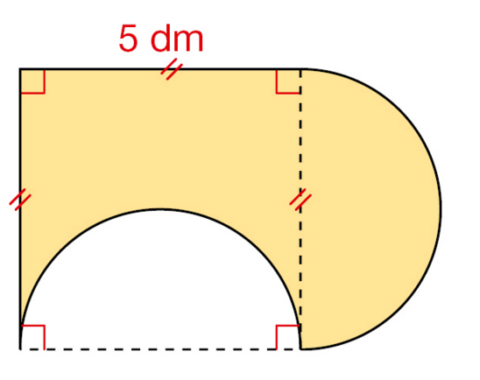
Exercice 14 :

Yann a utilisé 3 L de peinture pour peindre un disque de 2 m de rayon.
Mathias achète 6 L de la même peinture.
Déterminer mentalement s’il peut peindre le mur rectangulaire représenté ci-dessous.

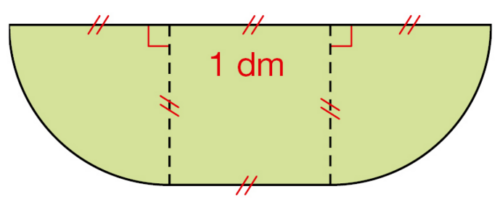
Exercice 15 :

En prenant 3,14 pour , calculer une valeur approchée de l’aire, en dm², de la surface verte
représentée ci-dessous.

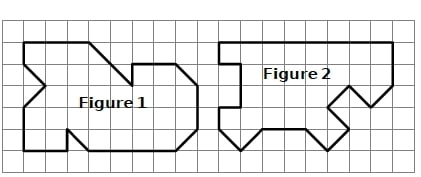
Exercice 16 :
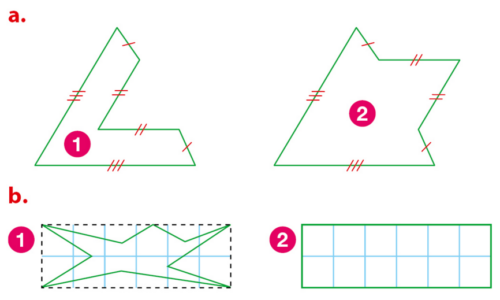
Parmi les figures 1 et 2,
1. Quelle est celle qui a le plus grand périmètre ? Justifie.

2. Quelle est celle qui a la plus grande aire ?Justifie.

.

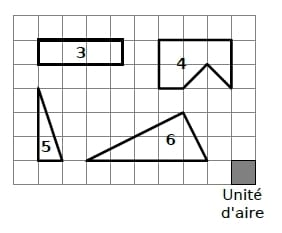
Exercice 17 :
Donne, en unités d’aire, les aires des figures 3 à 6.

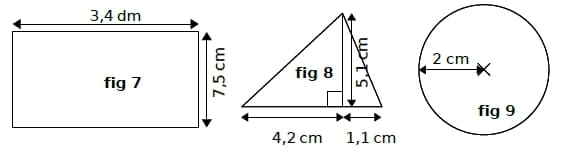
Exercice 18 :

1.  En détaillant tes calculs, donne en cm les périmètres des figures 7 et 9. Pour la figure 9, tu donneras une valeur approchée au dixième.
2. En détaillant tes calculs, donne en cm² les aires des figures 7,8 et 9. Pour la figure 9, tu donneras une valeur approchée au centième.

Exercice 19 :

1. Un rectangle a pour longueur 7 cm et pour aire 8,4 cm². Quelle est sa largeur ?
2. BUT est un triangle rectangle en U tel que BU = 3,4 cm et UT = 5,3 cm. Quelle est son aire en
   cm² ?
3. Une salle de classe a la forme d’un carré de côté 6,2 m. Quelle est son aire en dam² ? En dm² ?

Exercice 20 :
1. Sur ta copie, trace un triangle d’aire 12 cm².
2. Sur ta copie, trace un rectangle d’aire 18 cm² et de périmètre 38 cm.

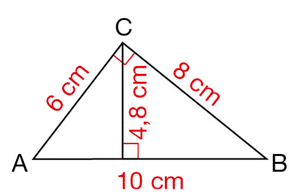
Exercice 21 :

ABC est un triangle rectangle en C.
a. Quel calcul permet C d’obtenir le périmètre du triangle ABC ?
b. Proposer deux méthodes différentes pour calculer l’aire du triangle ABC.

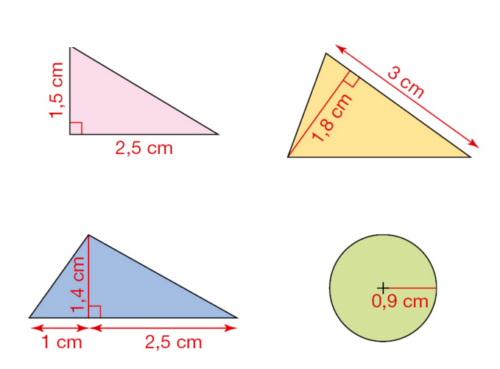
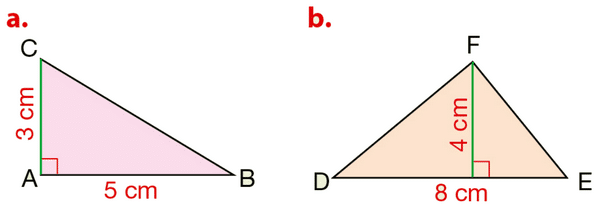
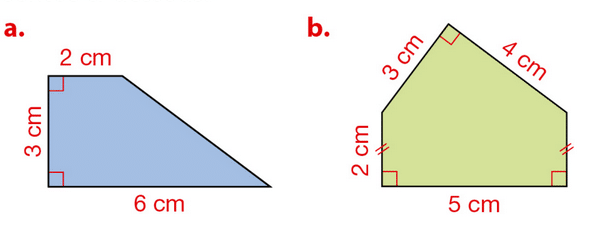
Exercice 22 :

Calculer mentalement l’aire de chaque triangle représenté.

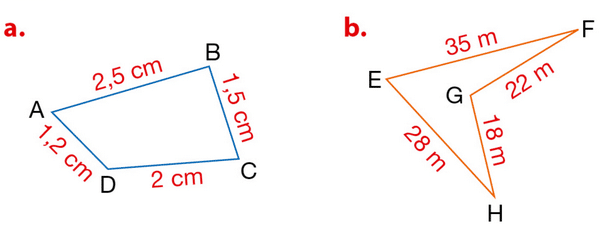
Exercice 23 :

Calculer le périmètre de chaque polygone représenté.

Exercice 24 :

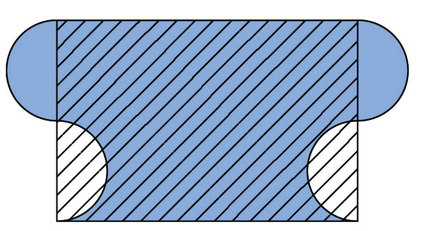
a. Comparer le périmètre du domaine coloré en bleu à celui du domaine hachuré.
b. Comparer l’aire du domaine coloré en bleu à celle du domaine hachuré.

Exercice 25 :

Calculer l’aire de chaque surface colorée représentée ci-dessous.

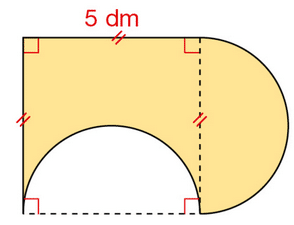
Exercice 26 :

Calculer l’aire, en dm², de la surface colorée représentée ci-dessous

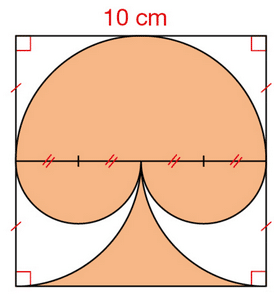
Exercice 27 :

Calculer une valeur approchée au centième près de l’aire, en cm², de ce «champignon » inscrit
dans un carré.

---

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «aires et périmètres : exercices de maths en 6ème corrigés en PDF.» au format PDF.

     

---

Nos applications

Téléchargez gratuitement la dernière version de nos applications.

---

OK

 Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.