Brevet Amérique du Nord 2021 maths : sujet et corrigé en PDF.
DIPLOME NATIONAL DU BREVET
AMERIQUE DU NORD 2021
MATHÉMATIQUES
Série générale
Durée de l’épreuve : 2 h 00 – 100 points
Exercice 1 (26 points)
Pour chacune des six affirmations suivantes, indiquer sur la copie, si elle est vraie ou fausse.
On rappelle que chaque réponse doit être justifiée.
1) On considère la fonction f définie par f (x) = 3x — 7
Affirmation n° l : « l’image par f du nombre —1 est 2 ».
2) On considère l’expression E = (x — 5)(x + 1).
Affirmation n° 2 : « L’expression E a pour forme développée et réduite ».
3) n est un nombre entier positif.
Affirmation n° 3 : « lorsque n est égal à 5, le nombre est un nombre premier».
4) On a lancé 15 fois un dé six faces numérotées de 1 6 et on a noté les fréquences
d’apparition dans le tableau ci-dessous :
Affirmation n° 4 : « la fréquence d’apparition du 6 est 0 ».
5) On considère un triangle RAS rectangle en S.
Le côté [AS] mesure 80 cm et l’angle mesure 26°.
Affirmation n° 5 : «le segment [RS] mesure environ 164 cm ».
6) Un rectangle ABCD a pour longueur 160 cm et pour largeur 95 cm.
Affirmation n° 6 : les diagonales de ce rectangle mesurent exactement 186 cm.
Exercice 2 (21 points)
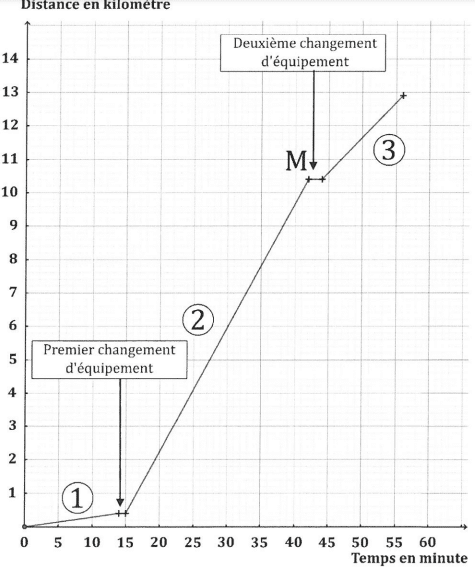
Une athlète a réalisé un triathlon d’une longueur totale de 12,9 kilomètres.
Les trois épreuves se déroulent dans l’ordre suivant :
Entre deux épreuves, l’athlète doit effectuer sur place un changement d’équipement.
Le graphique ci-dessous représente la distance parcourue (exprimée en kilomètre) par
l’athlète, en fonction du temps de parcours (exprimé en minute) de l’athlète pendant son triathlon.
Le point M a pour abscisse 42 et pour ordonnée 10,4.
A l’aide du tableau ci-dessus ou par lecture du graphique ci-dessus avec la précision qu’il permet, répondre aux questions suivantes, en justifiant la démarche.
1) Au bout de combien de temps l’athlète s’est-elle arrêtée pour effectuer son premier
changement d’équipement ?
2) Quelle est la longueur, exprimée en kilomètre, du parcours de l’épreuve de cyclisme ?
3) En combien de temps l’athlète a-t-elle effectué l’épreuve de course à pied ?
4) Parmi les trois épreuves, pendant laquelle l’athlète a été la moins rapide ?
5) On considère que les changements d’équipement entre les épreuves font partie du
triathlon.
La vitesse moyenne de l’athlète sur l’ensemble du triathlon est-elle supérieure à 14
km/h ?
Exercice 3 (16 points)
Dans cet exercice, aucune justification n ‘est demandée.
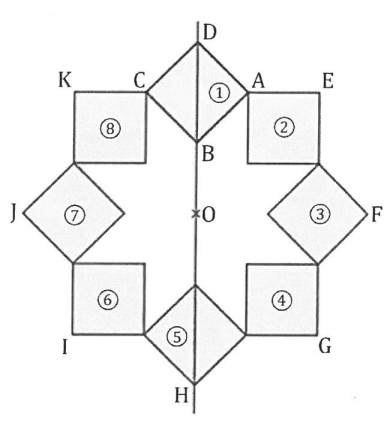
On a construit un carré ABCD.
On a construit le point O sur la droite (DB), à l’extérieur du segment [DB] et tel que : OB = AB.
Le point H est le symétrique de D par rapport à O.
On a obtenu la figure ci-dessous en utilisant plusieurs fois la même rotation de centre O et d’angle 45°.
La figure obtenue est symétrique par rapport à l’axe (DB) et par rapport au point O.
1)Donner deux carrés différents, images l’un de l’autre par la symétrie axiale d’axe (DB).
2) Le carré 3 est-il l’image du carré 8 par la symétrie centrale de centre O ?
3) On considère la rotation de centre O qui transforme le carré 1 en le carré 2.
Quelle est l’image du carré 8 par cette rotation ?
4) On considère la rotation de centre O qui transforme le carré 2 en le carré 5.
Préciser l’image du segment [EF] par cette rotation.
Exercice 4 (16 points)
Dans cet exercice, aucune justification n ‘est demandée.
On dispose d’un tableau carré ci-dessous partagé en neuf cases blanches de mêmes
dimensions qui constituent un motif.

Quatre instructions A, B, C et E permettent de changer l’aspect de certaines cases, lorsqu’on applique ces instructions. Ainsi :
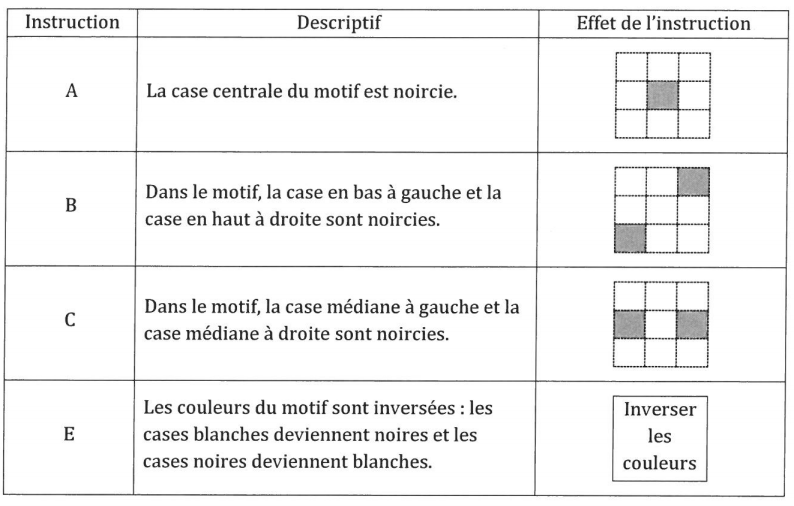
Remarque : si une case du motif est déjà noire et une instruction demande à la noircir, alors cette case ne change pas de couleur et reste noire à la suite de cette instruction.
Exemples : à partir d’un motif dont toutes les cases sont blanches :
La suite d’instructions A – C permet d’obtenir ce motif :
La suite d’instructions A – C – E permet d’obtenir ce motif :
1) Représenter le motif Obtenu avec la suite d’instructions A – B.
2) Parmi les quatre propositions suivantes, deux propositions permettent
d’obtenir le motif ci-dessous.
Lesquelles ?
Proposition n° 1 : A B C
Proposition n° 2 : C E
Proposition n° 3 : B C E C
Proposition n° 4 : C A E A
3) Donner une suite d’instructions qui permet d’obtenir le motif ci-dessous.
Exercice 5 (21 points)
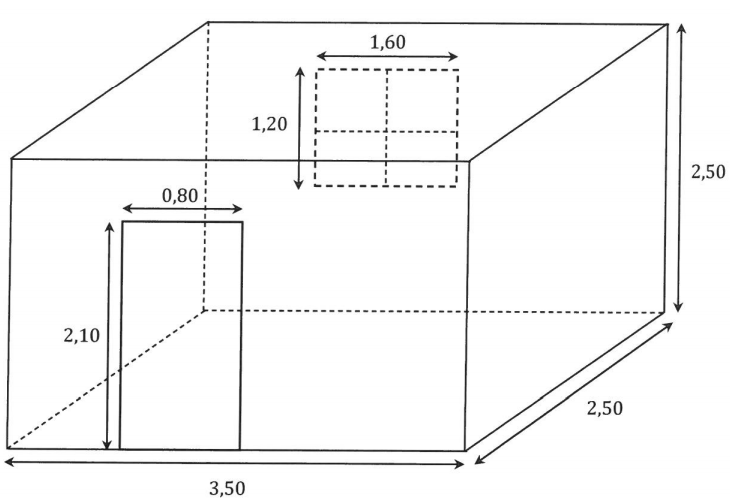
On souhaite rénover une salle de bain qui a la forme d’un parallélépipède rectangle.
II faut coller du papier peint sur les quatre murs.
On n’en colle pas sur la porte, ni sur la fenêtre.
Voici un schéma de la salle de bain, les dimensions sont exprimées en mètre :
On dispose des informations suivantes :
1)Montrer que la surface à recouvrir de papier peint est de 26,4 m².
2) Calculer le prix, en euro, d’un mètre carré de papier peint. Arrondir au centime d’euro.
3) Si on suit les conseils du vendeur, combien coûtera la rénovation de la salle de bain ?
4) Le jour de l’achat, une remise de 8 % est accordée.
Quel est le prix à payer après remise ? Arrondir au centime d’euro.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet Amérique du Nord 2021 maths : sujet et corrigé en PDF.» au format PDF.
D'autres cours et exercices à consulter
- Polynésie Française : brevet de maths 2022 avec sujet et corrigé
- Brevet de maths 2024 aux centres étrangers avec sujet et corrigé.
- Asie et Pacifique : brevet de maths 2022 avec sujet et corrigé
- Brevet Maths 2021 : sujet et corrigé du brevet blanc de maths
- Brevet Maths 2021 : sujet corrigé blanc pour la révision du DNB
- Brevet Maths 2021 : sujet blanc pour réviser le brevet
- Brevet de maths 2022 aux centres étrangers : sujet et corrigé du brevet.
- Brevet de maths 2017 : sujet blanc