Calcul littéral : exercices de maths en 4ème corrigés en PDF.
Mis à jour le 27 décembre 2025
Exercice 1 :
Ecrire sans parenthèses les expressions données :
a. -(3+x)
b. -(2a+4)
c. -(-3+x)
d. -(5-x)
e. -(7-2y)
f. -(-6-4x)
Exercice 2 :
Réduire chacune des expressions suivantes :
a.
b.
c.
d.
e.
f.
g.
h.
i.
j.
Exercice 3 :
Supprimer les parenthèses puis réduire chaque expression.
a.
b.
c.
d.
e.
f.
g.
Exercice 4 :
Développer puis réduire les expressions.
a.
b.
c.
d.
e.
f.
Exercice 5 :
Développer puis réduire les expressions.
a.
b.
c.
d.
e.
f.
g.
Exercice 6 :
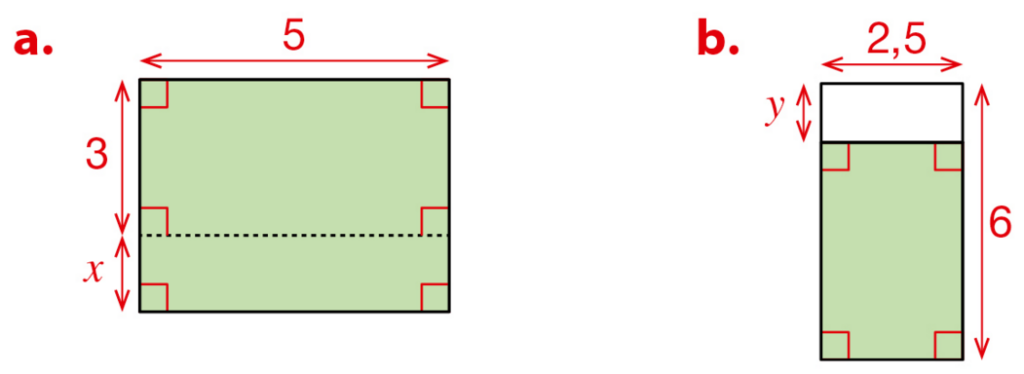
Dans cet exercice désigne un nombre supérieur à 3.
On se propose d’exprimer l’aire de la surface coloriée en fonction de
1.a. Expliquer pourquoi l’aire :
• du rectangle ABCD peut s’écrire ;
• du rectangle AEFG peut s’écrire .
b. Après avoir développé les expressions littérales précédentes, exprimer l’aire en fonction de
.
• Montrer que l’aire peut s’écrire aussi :
.
• Développer puis réduire cette expression.
3.Calculer alors la valeur de pour
.
Exercice 7 :développement d’expressions algébriques
A = x (x + 2)
B = 5x (x +3)
C = 2x (3x – 5)
D = – 3x (1 – 4x)
E = (x + 2) (-x + 3)
F = (2x + 3) (4x – 1)
G = (5 – 3y) (6 – 2y)
Exercice 8 : Développer et réduire.
A = (x + 3) (x – 2) + (2x + 4) (x + 5)
B = (2x – 1) ( 7x + 8) – (5 – 4x) (3x + 1)
C = (3x + 4) ( 7x – 1) – (2x + 5) (3x – 2)
Exercice 9 :
A = (x – 3) (3x – 1) – 2x² + 4
Calculer A pour : x = 2 x = -1
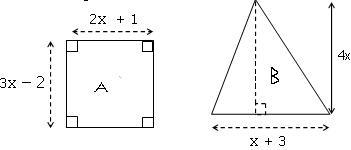
Exercice 10 :
Exprimer sous forme développée et réduite l’aire de ces deux figures.
Exercice 11 :
Factoriser en recherchant un facteur commun.
A = 11n + 11
B = x ² + 5x
C = 14t² – 21t
D = (x + 5)(x + 8 ) + 2 (x + 5)
E = (2x – 9) (3x + 7) + (2x – 9) (6 – 2x)
F = (5x – 3) (7x – 9) – (3x + 4) (5x – 3)
G = (7x + 1) ² + (7x + 1) (2x + 5)
H = (2a +3) (5a – 1) – (2a +3)²
Exercice 12 -Activité d’introduction au calcul littéral
On représente par étape des maisons à l’aide d’allumettes comme cela est fait ci-dessous.
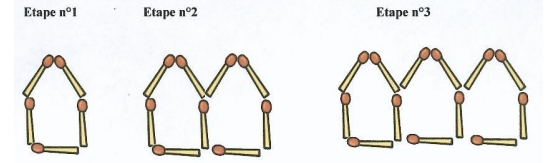
1. Combien faudra-t-il d’allumettes aux étapes n°4 et n°10 ? Répondre sans faire de dessin.
2. Vérifier si vous aviez trouvé le bon nombre
3. Combien d’allumettes faudra-t-il à l’étape n° 2007 ?
4. Comment exprimer le nombre d’allumettes pour une étape quelconque ?
Exercice 13 -Introduction au calcul littéral
Le professeur a écrit au tableau l’exercice suivant :
Calculer
23 × 7 + 3 ;
23 × 8 + 3;
23 × 9 + 3;
23 × 10 + 3
23 × 11 + 3;
23 × 12 + 3;
23 × 13 + 3;
23 × 14 + 3
Un camarade est absent.
Quelle consigne lui donner au téléphone, sans lui dicter tous les calculs.
La consigne est bonne si le camarade sait exactement ce qu’il doit faire.
Exercice 14 -Calcul d’une vitesse moyenne
1) Un randonneur parcourt 5 km en 1 heure et 15 minutes. Quelle est sa vitesse moyenne en km/h ?
Justifier
2) Une voiture roule à la vitesse de 50 km/h. En combien de temps parcourt-elle 110 kilomètres ? Donner
le résultat en heures et minutes.
Exercice 15 -Donner l’expression littérale
a désigne un nombre décimal non nul .
Donner une expression littérale de :
1) le double du carré de a .
2) le carré du double de a .
3) la moitié du carré de a :
4) le carré de la moitié de a .
5) le carré de l’opposé de a .
6) l’opposé du carré de a .
7) le carré de l’inverse de a .
8) l’inverse du carré de a .
Exercice 16 -Appliquer les propriétés et règles de calcul
1. Simplifier les écritures suivantes :
2. développer et réduire les expressions suivantes :
Exercice 17 -Salle de concert
Une salle de concert peut contenir 600 places. Il y a x places assises et les autres sont debout. Les places debout coûtent 15€ et les places assises 25€.
1°) Que représentent les expressions : a- 600 – x ? b- 25x ? c- 15 (600 – x) ?
2°) Exprime, en fonction de x la recette totale en euros si toutes les places sont occupées.
3°) Calcule cette recette si x = 200.
4°) Quel est le nombre de places assises si la salle est comble et si la recette est de 12 500 € ?
Exercice 18 -Développer les expressions suivantes
A = 6 (2x + 8) B = 7 (5x − 1) C = -4x (x − 9)
D = (3x + 4) (2x + 3) E = (7x + 5) (5x + (-3)) F = (2x + 9) (7x − 1)
Exercice 19 -Programme de calcul
On donne un programme de calcul :
Choisir un nombre.
Lui ajouter 2
Multiplier la somme obtenue par le nombre choisi
Ajouter 1 à ce produit
Ecrire le résultat.
1) Ecrire les calculs permettant de vérifier que si l’on fait fonctionner ce programme avec le nombre – 1 , on obtient 0.
2) Donner le résultat fourni par le programme lorsque le nombre choisi est -6
3) Donner le résultat fourni par le programme lorsque le nombre choisi est 4
4) Ecrire l’expression obtenue pour un nombre a quelconque.
Exercice 20 -Développer et réduire
a) Supprimer les parenthèses puis réduire l’expression M
b) Développer et réduire N et P.
c) Calculer N lorsque x est égal à 3.
Exercice 21 -Programme de calcul de mr Hamraoui
Mr Hamraoui demande a Anna de suivre les instructions suivantes:
– Choisis un nombre ;
– Multiplie le par -11 ;
– Ajoute 8 ;
– Multiplie le résultat par -9 ;
– Ajoute le nombre choisi au départ ;
– Ajoute -28 ;
– Donne ton résultat .
Anna: Je trouve 400 .
M. Hamraoui : Tu avais donc choisi 5 au départ .
Quel est le truc de Mr Hamraoui ?
Exercice 22 -Introduction au calcul littéral et géométrie
Une piscine rectangulaire mesure 10 m sur 5 m.
On désire aménager tout autour une plage.
Cependant cette plage ne doit pas avoir une superficie trop importante pour ne pas coûter trop cher à la collectivité, mais ne doit pas être trop petite pour ne pas pénaliser les non baigneurs.
On estime que la superficie de la plage doit être comprise entre 110 et 120 .
On décide alors de faire un avant-projet de piscine, en notant le nombre désignant la largeur de la plage.
Le nombre devient alors ce que l’on appelle une inconnue .

1. Calculer l’aire de cette plage dans le cas où , puis dans le cas où
, et enfin
2. Dans chacun des cas précédents, peut-on lancer le projet de construction ? Pourquoi ?
3. Quelle méthode pouvez-vous proposer pour trouver une largeur de plage satisfaisante ?
Pour accélérer la recherche de cette largeur idéale, on essaie d’exprimer en fonction du nombre , l’aire de cette plage.
Deux équipes vont y travailler :
– Calculer l’aire du rectangle ABCD, à laquelle on retranche l’aire de la piscine.
– Assembler les éléments de la plage comme indiqué sur le croquis ci-dessous.

4. Retrouver les expressions obtenues par chacune des deux équipes.
5. Proposer une largeur possible de plage pour lancer le projet.
Exercice 23 -Développer et réduire les expressions suivantes :
Exercice 24 -Calculs contenant des parenthèses
Supprimer les parenthèses puis réduire les expressions :
Exercice 25 -Identités remarquables
En se rappelant que .
développer et réduire les expressions suivantes :
Exercice 26 -Calcul algébrique
Réduire chaque expression littérale suivante :
Exercice 27 :
Réduire chacune de ces expressions :
Exercice 28 :
1. Développer et réduire les expressions suivantes.
2. Tester le résultat pour x = 0 et x = 1.
a.
b.
Exercice 29 -Programme de calcul
Voici un programme de calcul :
– Choisir un nombre.
– Soustraire 3 à ce nombre.
– Multiplier le résultat obtenu par – 5 .
– Diviser le résultat obtenu par 4.
– Ajouter le nombre de départ au résultat obtenu.
1. Effectuer ce programme de calcul pour – 2 et pour 7.
2. Reprendre ce programme pour un nombre x.
Exercice 30 -Du texte à l’écriture mathématique
Écrire le plus simplement possible en fonction de x :
a. «le double de x augmenté de 1 » ;
b. «la somme de 3 et du triple de x » ;
c. «le tiers de x, diminué de 5 » ;
d. « le produit par 5 de la somme de x et de 4 » ;
e. «la somme de 6 et du produit de x par 7».
Développer et réduire les expressions suivantes :
Exercice 31 -Réduire des expressions algébriques
Réduire chacune des expressions suivantes :
Exercice 32 -Suppression de parenthèses
Supprimer les parenthèses puis réduire les expressions suivantes :
Exercice 33 -Réduction d’expressions littérales
Réduire, si possible, les expressions suivantes :
Exercice 34 :
Ecrire de la façon la plus simple les expressions suivantes :
Exercice 35 :
Développer et réduire les expressions suivantes :
f. (3a – 4)(4a – 11)
k. (- a + 5b)(4b + 3a)
Exercice 36 :
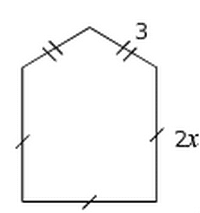
Déterminer le périmètre de la figure ci-dessous en fonction de x.
Exercice 37 :
En utilisant la propriété de la double distributivité, développer et réduire les expressions littérales suivantes :
C = ( x + 2 ) ( x – 5 )
D = ( x + 3 ) ( x – 6 ) E = ( x + 6 ) ( x – 8 ) F = ( x – 3 ) ( x + 4 )
G = ( x – 7 ) ( x – 4 ) H = ( x – 1 ) ( x + 7 ) I = ( 2 x + 7 ) ( 3 x + 8 )
Exercice 38 :
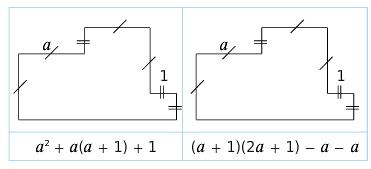
On souhaite exprimer l’aire de la figure ci-dessous, en fonction de a.
1.Voici deux propositions. Indiquer le découpage utilisé pour obtenir l’expression donnée.
2.Proposer une autre expression.
3.Montrer que les différentes expressions peuvent s’écrire 2a²+a+1.
Exercice 39 :
Voici deux programmes de calcul.
a. On choisit le nombre 2.
Calculer le nombre obtenu avec le programme A, puis avec le programme B.
b. Serge affirme : « J’ai choisi un nombre et les deux programmes ont donné le même résultat ».
Déterminer le nombre choisi par Serge en résolvant une équation.
Exercice 40 :
Dans un magasin :
• Jordan achète 4 BD au même prix et un manga à 8 €.
• Piala achète 2 de ces BD et un dictionnaire 45 €.
A la caisse, ils paient la même somme.
On se propose de déterminer le prix p, en euros, de chaque BD.
1. Exprimer en fonction de p, le montant :
a. de la dépense de Jordan,
b. de la dépense de Piala.
2. Déterminer p en résolvant une équation.
Exercice 41 :
A vélo, Dylan a fait trois tours du lac puis il a parcouru 7 km en forêt.
Loris n’a fait qu’un seul tour du lac mais il a parcouru 16 km en forêt.
A leur arrivée, ils constatent qu’ils ont parcouru la même distance totale.
Voici un schéma qui représente la situation.
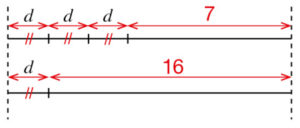
a. Que représente l’inconnue d sur ce schéma ?
b. Calculer mentalement la valeur de d. Interpréter ce résultat.
Exercice 42 :
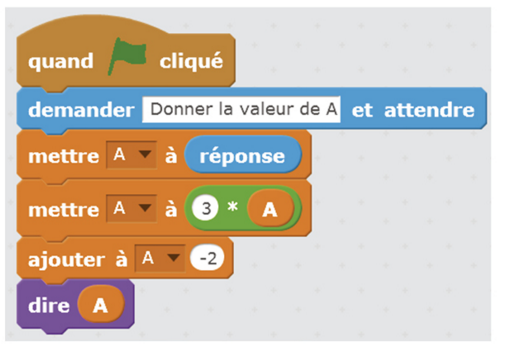
Voici un programme écrit avec le langage Scratch.
a. Que permet de faire ce programme ?
b. Quelle valeur annonce le lutin la fin du programme si l’on saisit 5 au début ?
c. Quelle valeur a-t-on saisie au début du programme si le lutin annonce 4 à la fin ?
Exercice 43 :
Dans chaque cas, citer l’inconnue et dire s’il s’agit ou non d’une équation du premier degré.
Exercice 44 :
Voici un programme de calcul.

On note x le nombre choisi au départ.
1.a. Exprimer en fonction de x le nombre N obtenu avec ce programme.
b. Développer et réduire cette expression.
c. Factoriser cette expression.
2. Calculer N pour : x = 0 puis x = 2.
Exercice 45 :
Voici un programme de calcul.
On note le nombre choisi au départ.
1.a. Exprimer en fonction de le nombre
obtenu avec ce programme.
b. Réduire cette expression.
c. Factoriser cette expression.
2. Calculer pour :
puis
.
Exercice 46 :
On considère ce rectangle dont les côtés ont des longueurs variables exprimées dans la même unité.
x désigne un nombre positif.
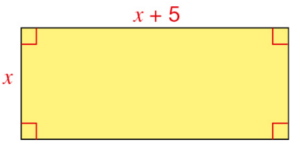
a. Que désigne pour ce rectangle chacune de ces expressions ?
Répondre éventuellement « rien ».
b. Calculer le périmètre de ce rectangle pour x = 3, puis pour x = 7,5.
c. Calculer l’aire de ce rectangle pour x = 4, puis pour x = 10.
Exercice 47 :
Dans chaque cas, dire si l’affirmation est vraie ou fausse. Justifier.
a. « Pour
, A est égal à 30. »
b. « Pour
, B est égal à 18. »
c. «Pour
, C est égal à 1.»
Exercice 48 :
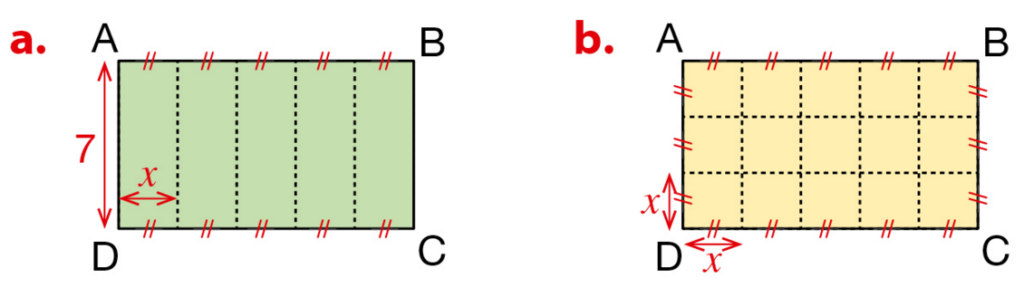
1. Dans chaque cas, exprimer l’aire du rectangle ABCD en fonction de x.
2. Dans chaque cas, calculer l’aire du rectangle ABCD pour x = 6.
Exercice 49 :
Dans chaque cas, donner l’aire du rectangle coloré en vert sous forme d’un produit et sous forme
d’une somme algébrique.
Exercice 50 :
Sur cette figure, le côté de ce carré a une longueur x, en cm, variable avec x < 6.
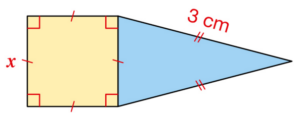
a. Que désigne pour cette figure chacune de ces expressions ?
b. Tester l’égalité B = C pour :
.
Exercice 51 :
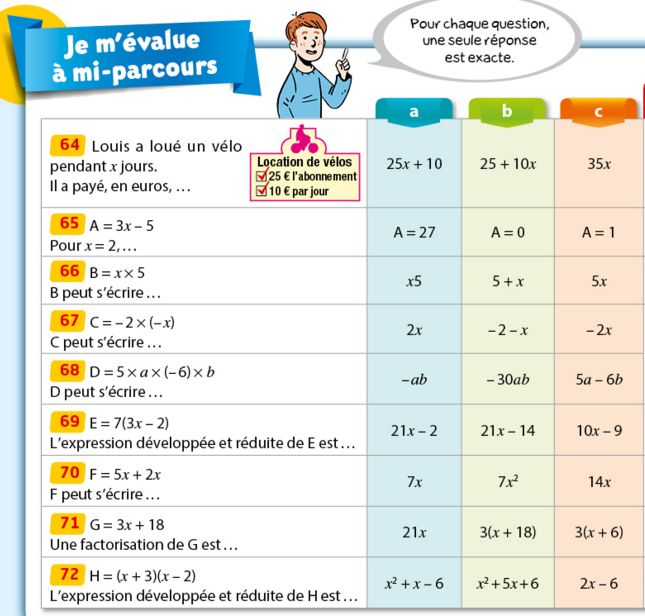
Effectuer ce QCM sur le calcul littéral.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «calcul littéral : exercices de maths en 4ème corrigés en PDF.» au format PDF.
Ressources de quatrième
Cours de quatrième
Exercices de quatrième
D'autres cours et exercices à consulter
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.