Fractions et calculs : cours de maths en 4ème en PDF.

Mis à jour le 23 avril 2025

Accueil >> Collège >> Maths 4ème >> Cours de maths >> Cours en 4ème >> Fractions et calculs : cours de maths en 4ème en PDF.
🧮Cours de Mathématiques
4ème • Collège
Fractions et calculs
📖 Temps de lecture : 5 min
🎯 Niveau : Collège
📱 Format : Gratuit
📄 PDF : Disponible
Les fractions dans un cours de maths en 4ème où nous aborderons les quatre opérations (addition, soustraction, multiplication et division) et la résolution de problèmes dans cette leçon destinés aux élèves de quatrième au cycle 4.Ce chapitre intervient après avoir assimilé les nombres relatifs.

I. Définition et vocabulaire :

1. Définition :

Définition :

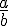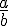Une fraction est  le quotient de deux entiers relatifs écrit sous la forme \frac{a}{b} .

\frac{a}{b}  est le nombre tel que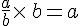 \frac{a}{b}\times \,b=a

Lorsque a ou b n’est pas un entier, le quotient est une écriture fractionnaire.

2. Vocabulaire :

Définition :
\star\, a est le « numérateur » de la fraction .
\star\, b est le « dénominateur » de la fraction .

Exemple :

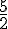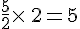\frac{5}{2} est le nombre tel que \frac{5}{2}\times \,2=5 .

3. Egalités de fractions :

Propriété :

La valeur d’une fraction n’est pas modifiée si l’on multiplie ou divise son numérateur et son dénominateur par le même nombre.
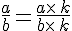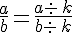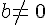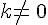\frac{a}{b}=\frac{a\times \,k}{b\times \,k} et \frac{a}{b}=\frac{a: \,k}{b: \,k} ( avec b\neq\,0 et k\neq\,0 ).

4. Inverse d’une fraction :

Définition :

L’inverse du nombre a est le nombre b tel que 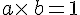a\times \,b=1  .

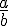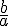L’inverse de la fraction \frac{a}{b}  est la fraction  \frac{b}{a} .

II. Opérations sur les fractions :

1. Addition de fractions :

Règle n° 1 :

On additionne deux fractions ayant le même dénominateur en additionnant les deux

numérateurs et en conservant le dénominateur commun.

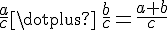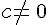\frac{a}{c}+\,\frac{b}{c}=\frac{a+b}{c} (avec c\neq\,0 ).

Exemple :

\frac{5}{3}+\,\frac{11}{3}=\,\frac{5+11}{3}=\,\frac{16}{3}

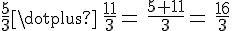
2. Soustraction de fractions :

Règle n° 2 :

On soustrait deux fractions ayant le même dénominateur en soustrayant les deux

numérateurs et en conservant le dénominateur commun .

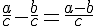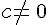\frac{a}{c}-\frac{b}{c}=\frac{a-b}{c}    (avec c\neq\,0 ).

Exemple :

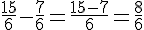
\frac{15}{6}-\frac{7}{6}=\frac{15-7}{6}=\frac{8}{6}

Règle n° 3 :

Pour additionner ou soustraire deux fractions n’ayant pas le même dénominateur, on réduit d’abord ces deux fractions au même dénominateur (voir I.2.)  puis on effectue l’addition ou la soustraction en appliquant la règle 1 ou 2.

Exemples :

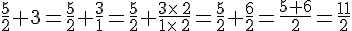
\frac{5}{2}+3=\frac{5}{2}+\frac{3}{1}=\frac{5}{2}+\frac{3\times \,2}{1\times \,2}=\frac{5}{2}+\frac{6}{2}=\frac{5+6}{2}=\frac{11}{2}

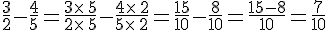
\frac{3}{2}-\frac{4}{5}=\frac{3\times \,5}{2\times \,5}-\frac{4\times \,2}{5\times \,2}=\frac{15}{10}-\frac{8}{10}=\frac{15-8}{10}=\frac{7}{10}

3. Multiplication de deux fractions :

Règle n° 4 :

On effectue le produit de deux fractions en multipliant les deux numérateurs entre eux et les deux dénominateurs entre eux.

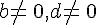\frac{a}{b}\times \,\frac{c}{d}=\frac{a\times \,c}{b\times \,d} (avec b\neq\,0,d\neq\,0 ).

Exemples :

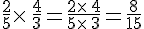
\frac{2}{5}\times \,\frac{4}{3}=\frac{2\times \,4}{5\times \,3}=\frac{8}{15}

4. Division de deux fractions :

Règle n° 5 :

Diviser deux fractions revient à multiplier la première par l’inverse de la seconde .

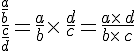
\frac{\frac{a}{b}}{\frac{c}{d}}=\frac{a}{b}\times \,\frac{d}{c}=\frac{a\times \,d}{b\times \,c}

Exemple :

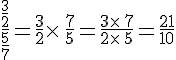
\frac{\frac{3}{2}}{\frac{5}{7}}=\frac{3}{2}\times \,\frac{7}{5}=\frac{3\times \,7}{2\times \,5}=\frac{21}{10}

Vous avez assimilé le cours sur les fractions en 4ème ?

Effectuez ce QCM de maths en quatrième sur les fractions afin d’évaluer vos acquis sur cette leçon.

Les fractions

QCM sur les fractions en quatrième.


Un autre QCM sur les opérations sur les fractions.
Fractions et opérations

QCM sur les fractions et opérations en quatrième.

4.7/5 - (27764 votes)
Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «fractions et calculs : cours de maths en 4ème en PDF.» au format PDF.

Ressources de quatrième

Cours de quatrième

cours maths 4ème
Calcul littéral et la double distributivité
cours maths 4ème
Proportionnalité et pourcentages
cours maths 4ème
Translation et rotation
cours maths 4ème
Théorème de Pythagore
cours maths 4ème
Puissances de 10
cours maths 4ème
Les équations

Exercices de quatrième

exercices maths 4ème
Calcul littéral
exercices maths 4ème
Théorème de Pythagore
exercices maths 4ème
Fractions
exercices maths 4ème
Les équations
exercices maths 4ème
Volumes de pyramides et cônes
exercices maths 4ème
Nombres relatifs
×12

L'équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs
200+ Années cumulées
Quotidien Mise à jour

Nos ressources pédagogiques

📚 Les cours ✏️ Les exercices 🎓 Brevet 🏆 Bac
Nos applications

Téléchargez gratuitement la dernière version de nos applications.
Application Mathovore sur Google Play Store. Application Mathovore sur Apple Store.

Inscription gratuite à Mathovore.  Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.