Brevet de maths en France 2019 : sujet et corrigé à télécharger en PDF

DIPLÔME NATIONAL DU BREVET
SESSION 2019
MATHEMATIQUES
Série générale
Durée de l’épreuve : 2 h 00 100 points

Exercice 1 : ( 10 points )
Le capitaine d’un navire possède un trésor constitué de 69 diamants, 1 150 perles et 4 140 pièces d’or.
1. Décomposer 69 ; 1 150 et 4 140 en produits de facteurs premiers.
2. Le capitaine partage équitablement le trésor entre les marins.
Combien y-a-t-il de marins sachant que toutes les pièces, perles et diamants ont été distribués ?

Exercice 2 : ( 19 points )
Dans cet exercice, on donnera, si nécessaire, une valeur approchée des résultats au centième près.
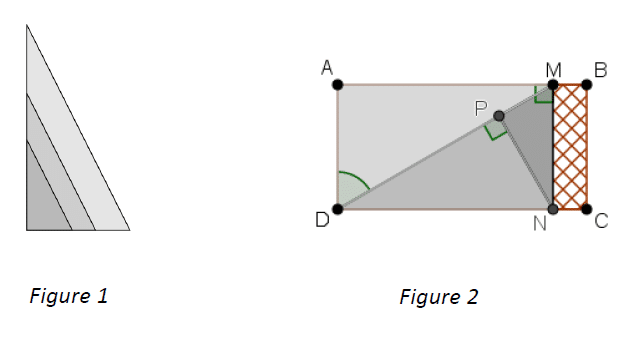
Pour construire le décor d’une pièce de théâtre (Figure 1), Joanna dispose d’une plaque rectangulaire ABCD de 4 m sur 2 m dans laquelle elle doit découper les trois triangles du décor avant de les superposer.

Elle propose un découpage de la plaque (Figure 2).

Le triangle ADM respecte les conditions suivantes :

Le triangle ADM est rectangle en A
AD=2 m
$\widehat{ADM}=60^{\circ}$

1. Montrer que [AM] mesure environ 3,46 m.
2. La partie de la plaque non utilisée est représentée en quadrillé sur la figure 2. Calculer une valeur approchée au centième de la proportion de la plaque qui n’est pas utilisée.
3. Pour que la superposition des triangles soit harmonieuse, Joanna veut que les trois triangles AMD, PNM et PDN soient semblables.

Démontrer que c’est bien le cas.
4. Joanna aimerait que le coefficient d’agrandissement pour passer du triangle PDN au triangle AMD soit plus petit que 1,5.

Est-ce le cas ? Justifier.

Exercice 3 : ( 17 points )
Les questions 1 et 2 sont indépendantes.
Un sablier est composé de :
– Deux cylindres C₁ et C₂ de hauteur 4,2 cm et de diamètre 1,5 cm
– Un cylindre C3
– Deux demi-sphères S₁ et S₂ de diamètre 1,5 cm
On rappelle le volume d’un cylindre d’aire de base et de hauteur ℎ :
$V=B,\times ,h$ .

1.
a. Au départ, le sable remplit le cylindre C₂ aux deux tiers. Montrer que le volume du sable est
environ 4,95 .
b. On retourne le sablier. En supposant que le débit d’écoulement du sable est constant et égal à
1,98 , calculer le temps en minutes et secondes que va mettre le sable à s’écouler dans
le cylindre inférieur.
2. En réalité, le débit d’écoulement d’un même sablier n’est pas constant.
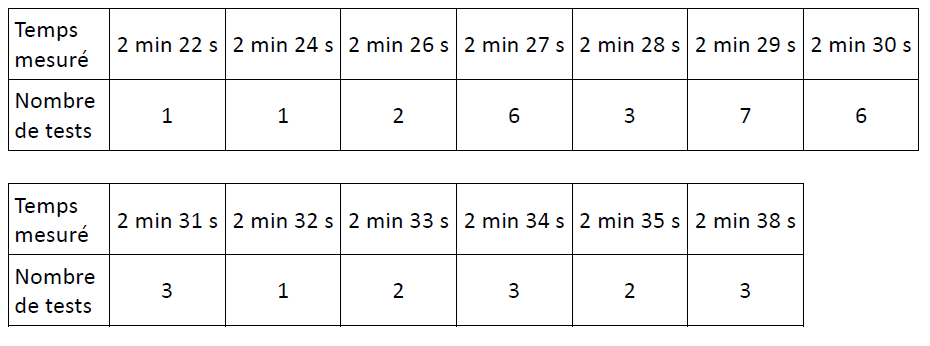
Dans une usine où on fabrique des sabliers comme celui-ci, on prend un sablier au hasard et on
teste plusieurs fois le temps d’écoulement dans ce sablier. Voici les différents temps récapitulés
dans le tableau suivant :

a. Combien de tests ont été réalisés au total ?
b. Un sablier est mis en vente s’il vérifie les trois conditions ci-dessous, sinon il est éliminé.
– L’étendue des temps est inférieure à 20 s
– La médiane des temps est comprise entre 2 min 29 s et 2 min 31 s
– La moyenne des temps est comprise entre 2 min 28 s et 2 min 32 s
Le sablier testé sera-t-il éliminé ?

Exercice 4 : ( 19 points )
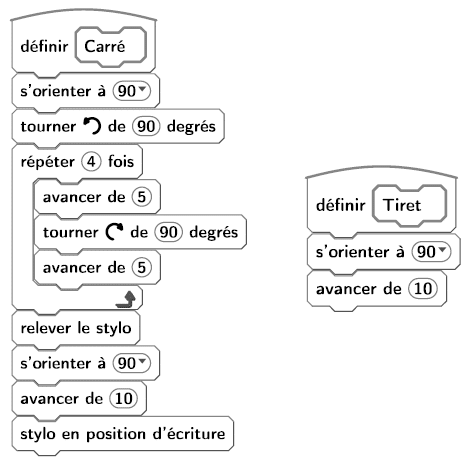
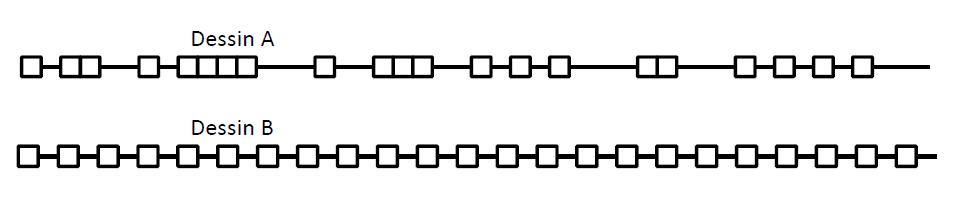
On veut réaliser un dessin constitué de deux types d’éléments (tirets et carrés) mis bout à bout.
Chaque script ci-contre trace un élément, et déplace le stylo.
On rappelle que « s’orienter à 90 » signifie qu’on oriente le stylo vers la droite.

1. En prenant 1 cm pour 2 pixels, représenter la figure obtenue si on exécute le script Carré.
Préciser les positions de départ et d’arrivée du stylo sur votre figure.
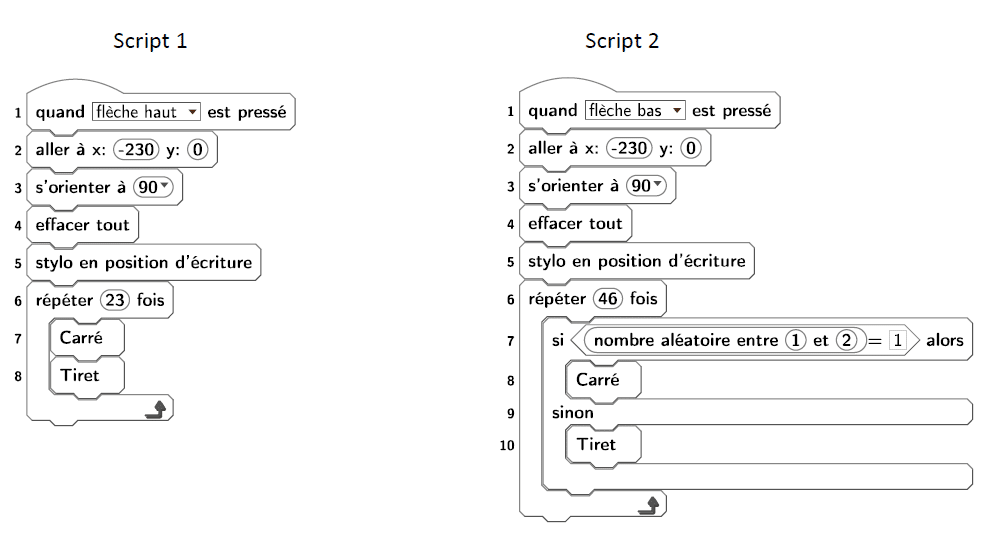
Pour tracer le dessin complet, on a réalisé 2 scripts qui se servent des blocs « Carré » et « Tiret »
ci-dessus :

On exécute les deux scripts et on obtient les deux dessins ci-dessous.

2. Attribuer à chaque script la figure dessinée. Justifier votre choix.
3. On exécute le script 2.
a. Quelle est la probabilité que le premier élément tracé soit un carré ?
b. Quelle est la probabilité que les deux premiers éléments soient des carrés ?
4. Dans le script 2, on aimerait que la couleur des différents éléments, tirets ou carrés, soit aléatoire,
avec à chaque fois 50 % de chance d’avoir un élément noir et 50 % de chance d’avoir un élément
rouge.
Écrire la suite d’instructions qu’il faut alors créer et préciser où l’insérer dans le script 2.

Exercice 5 : ( 18 points )
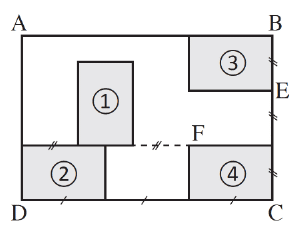
Olivia s’est acheté un tableau pour décorer le mur de son salon.
Ce tableau, représenté ci-dessous, est constitué de quatre rectangles identiques nommés 1, 2, 3 et 4 dessinés à l’intérieur d’un grand rectangle ABCD d’aire égale à 1,215 m².

Le ratio longueur : largeur est égal à 3 : 2 pour chacun des cinq rectangles.
1. Recopier, en les complétant, les phrases suivantes. Aucune justification n’est demandée.
a. Le rectangle … est l’image du rectangle … par la translation qui transforme C en E.
b. Le rectangle 3 est l’image du rectangle … par la rotation de centre F et d’angle 90° dans le
sens des aiguilles d’une montre.
c. Le rectangle ABCD est l’image du rectangle … par l’homothétie de centre … et de rapport 3.
(Il y a plusieurs réponses possibles, une seule est demandée.)

2. Quelle est l’aire d’un petit rectangle ?
3. Quelles sont la longueur et la largeur du rectangle ABCD ?

Exercice 6 : ( 17 points )
Voici deux programmes de calcul.

1. Vérifier que si on choisit 5 comme nombre de départ,
– Le résultat du programme 1 vaut 16.
– Le résultat du programme 2 vaut 28
On appelle le résultat du programme 1 en fonction du nombre choisi au départ.
La fonction $B:x,\mapsto ,(x-1)(x+2)$ donne le résultat du programme 2 en fonction du nombre choisi au départ.
2.
a. Exprimer en fonction de .
b. Déterminer le nombre que l’on doit choisir au départ pour obtenir 0 comme résultat du programme 1.
3. Développer et réduire l’expression :

4.
a. Montrer que .
b. Quels nombres doit-on choisir au départ pour que le programme 1 et le programme 2 donnent le même résultat ? Expliquer la démarche.

Consulter le corrigé en ligne

4.7/5 - (83 votes)

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet de maths en France 2019 : sujet et corrigé à télécharger en PDF» au format PDF.

D'autres cours et exercices à consulter

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.

D'autres cours et exercices à consulter

Laisser un commentaire