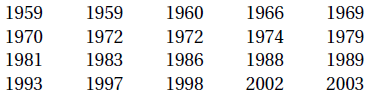Brevet maths 2019 : sujet blanc pour réviser en ligne.
Exercice 1 : 20 points.
Partie 1
On s’intéresse à une course réalisée au début de l’année 2018. Il y a 80 participants, dont 32 femmes
et 48 hommes.
Les femmes portent des dossards rouges numérotés de 1 à 32. Les hommes portent des dossards verts
numérotés de 1 à 48.
Il existe donc un dossard no 1 rouge pour une femme, et un dossard no 1 vert pour un homme, et ainsi
de suite …
1. Quel est le pourcentage de femmes participant à la course?
2. Un animateur tire au hasard le dossard d’un participant pour remettre un prix de consolation.
a. Soit l’événement V : « Le dossard est vert ». Quelle est la probabilité de l’événement V ?
b. Soit l’événement M : « Le numéro du dossard est un multiple de 10 ». Quelle est la probabilité
de l’événement M?
c. L’animateur annonce que le numéro du dossard est un multiple de 10. Quelle est alors la
probabilité qu’il appartienne à une femme?
Partie 2
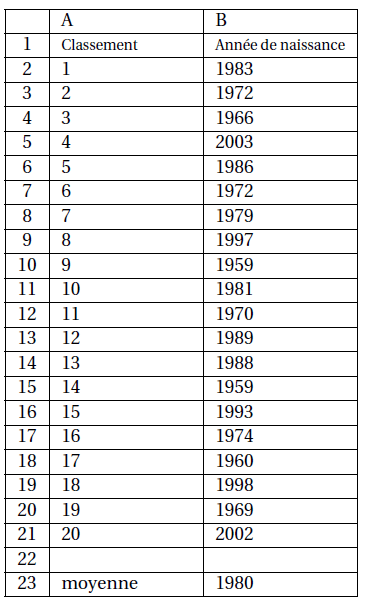
À l’issue de la course, le classement est affiché ci-dessous.
On s’intéresse aux années de naissance des 20 premiers
coureurs.
1. On a rangé les années de naissance des coureurs
dans l’ordre croissant :
Donner la médiane de la série.
2. La moyenne de la série a été calculée dans la cellule B23.
Quelle formule a été saisie dans la cellule B23?
3. Astrid remarque que la moyenne et la médiane de cette série sont égales.
Est-ce le cas pour n’importe quelle autre série statistique?
Expliquer votre réponse.
Exercice 2 : 11 points.
1. Le nombre 588 peut se décomposer sous la forme 588 = 22×3×72.
Quels sont ses diviseurs premiers, c’est-à-dire les nombres qui sont à la fois des nombres premiers
et des diviseurs de 588?
2. a. Déterminer la décomposition en facteurs premiers de 27 000 000.
b. Quels sont ses diviseurs premiers ?
3. Déterminer le plus petit nombre entier positif impair qui admet trois diviseurs premiers différents.
Expliquer votre raisonnement.
Exercice 3 : 13 points.
Après un de ses entraînements de course à pied, Bob
reçoit de la part de son entraîneur le récapitulatif de sa
course, reproduit ci-dessous.

L’allure moyenne du coureur est le quotient de la durée de la course par la distance parcourue et s’exprime en min/km.
Exemple : si Bob met 18 min pour parcourir 3 km, son allure est de 6 min/km.
Exercice 4 : 17 points.
Les abeilles ouvrières font des allers-retours entre les fleurs et la ruche pour transporter le nectar et
le pollen des fleurs qu’elles stockent dans la ruche.
1. Une abeille a une masse moyenne de 100 mg et rapporte en moyenne 80 mg de charge (nectar,
pollen) à chaque voyage.
Un homme a une masse de 75 kg. S’il se chargeait proportionnellement à sa masse, comme une
abeille, quelle masse cet homme transporterait-il ?
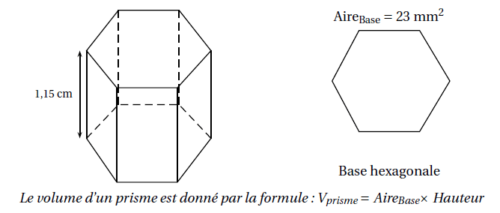
2. Quand elles rentrent à la ruche, les abeilles déposent le nectar récolté dans des alvéoles.
On considère que ces alvéoles ont la forme d’un prisme de 1,15 cm de hauteur et dont la base
est un hexagone d’aire 23 mm² environ, voir la figure ci-dessous.
a. Vérifier que le volume d’une alvéole de ruche est égal à 264,5 mm².
b. L’abeille stocke le nectar dans son jabot. Le jabot est une petite poche sous l’abdomen
d’un volume de litre. Combien de sorties au minimum l’abeille doit-elle faire pour
remplir une alvéole?
(rappel : 1 = 1 litre)
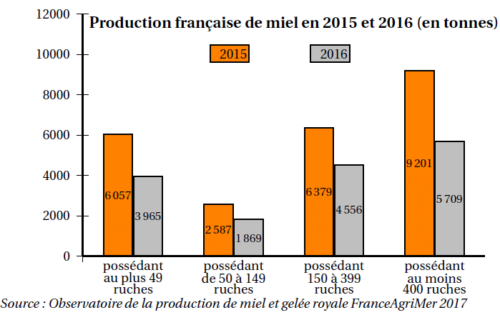
3. Le graphique ci-dessous présente la production française de miel en 2015 et 2016.
a. Calculer la quantité totale de miel (en tonnes) récoltée en 2016.
b. Sachant que la quantité totale de miel récoltée en 2015 est de 24 224 tonnes, calculer le
pourcentage de baisse de la récolte de miel entre 2015 et 2016.
Exercice 5 : 15 points.
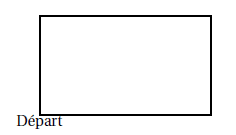
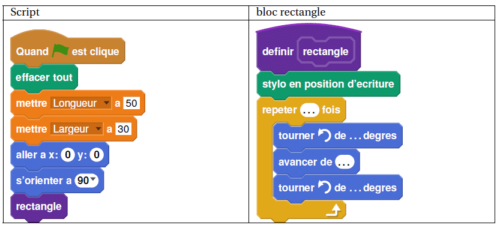
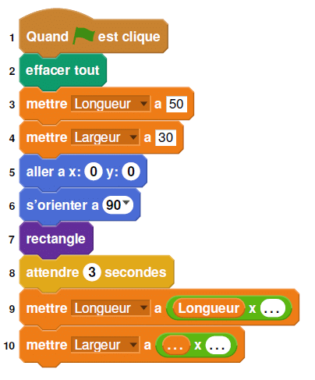
Sam a écrit le programme ci-dessous qui permet de tracer un rectangle
comme ci-contre.
Ce programme comporte deux variables (Longueur) et (Largeur) qui
représentent les dimensions du rectangle.
On rappelle que l’instruction 
1. Compléter le bloc rectangle ci-dessus avec des nombres et des variables pour que le script fonctionne.
On recopiera et on complétera uniquement la boucle répéter sur sa copie.
2. Lorsque l’on exécute le programme, quelles sont les coordonnées du point d’arrivée et dans
quelle direction est-on orienté?
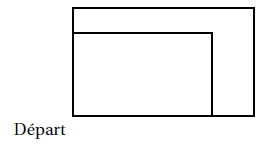
3. Sam a modifié son script pour tracer également l’image du rectangle par l’homothétie de centre
le point de coordonnées (0; 0) et de rapport 1,3.
a. Compléter le nouveau script de Sam donné ci-contre afin d’obtenir la figure ci-dessous.
On recopiera et on complétera sur sa copie les lignes 9 et 10 ainsi que l’instruction manquante
en ligne 11.
b. Sam exécute son script. Quelles sont les nouvelles valeurs des variables Longueur et Largeur
à la fin de l’exécution du script ?
Exercice 6 : 12 points.
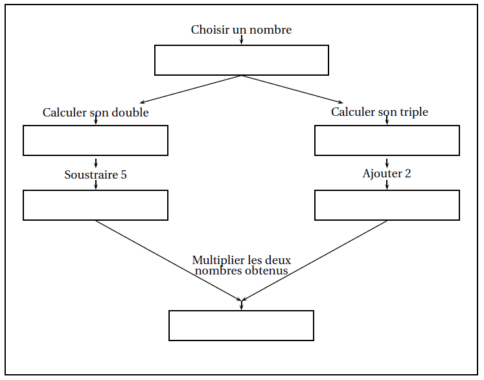
La figure ci-dessous donne un schéma d’un programme de calcul.
1. Si le nombre de départ est 1, montrer que le résultat obtenu est −15.
2. Si on choisit un nombre quelconque comme nombre de départ, parmi les expressions suivantes,
quelle est celle qui donne le résultat obtenu par le programme de calcul ? Justifier.
3. Lily prétend que l’expression donne les mêmes résultats que l’expression B pour toutes les valeurs de x.
L’affirmation de Lily est-elle vraie? Justifier.
Exercice 7 : 12 points.
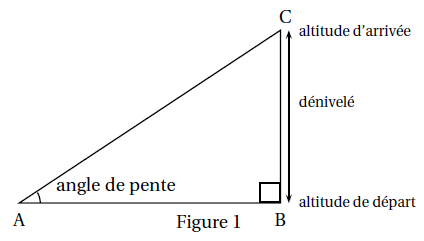
Pour la course à pied en montagne, certains sportifs mesurent leur performance par la vitesse
ascensionnelle, notée Va.
Va est le quotient du dénivelé de la course, exprimé en mètres, par la durée, exprimée en
heure.
Par exemple : pour un dénivelé de 4 500 met une durée de parcours de 3 h : Va = 1500 m/h.
Rappel : le dénivelé de la course est la différence entre l’altitude à l’arrivée et l’altitude au départ.
Un coureur de haut niveau souhaite atteindre une vitesse ascensionnelle d’au moins 1 400 m/h lors
de sa prochaine course.
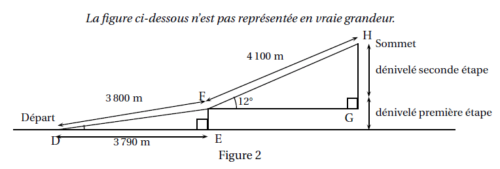
Le parcours se décompose en deux étapes (voir figure 2) :
• Première étape de 3 800 m pour un déplacement horizontal de 3 790 m.
• Seconde étape de 4,1 km avec un angle de pente d’environ 12°.
1. Vérifier que le dénivelé de la première étape est environ 275,5 m.
2. Quel est le dénivelé de la seconde étape?
3. Depuis le départ, le coureur met 48 minutes pour arriver au sommet.
Le coureur atteint-il son objectif ?
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet maths 2019 : sujet blanc pour réviser en ligne.» au format PDF.
D'autres cours et exercices à consulter
- Brevet Maths 2021 : sujet et corrigé du brevet blanc de maths
- Brevet de maths 2017 sujet 0
- Polynésie Française : brevet de maths 2022 avec sujet et corrigé
- Brevet de maths 2024 aux centres étrangers avec sujet et corrigé.
- Asie et Pacifique : brevet de maths 2022 avec sujet et corrigé
- Brevet Maths 2021 : sujet corrigé blanc pour la révision du DNB
- Brevet Maths 2021 : sujet blanc pour réviser le brevet
- Brevet de maths 2022 aux centres étrangers : sujet et corrigé du brevet.