Brevet Maths 2021 : sujet et corrigé du brevet blanc de maths

BREVET BLANC MATHÉMATIQUES

Session : janvier 2021

Durée de l’épreuve : 2 heures – 40 points dont 1 point pour le soin.

L’utilisation de la calculatrice est autorisée.

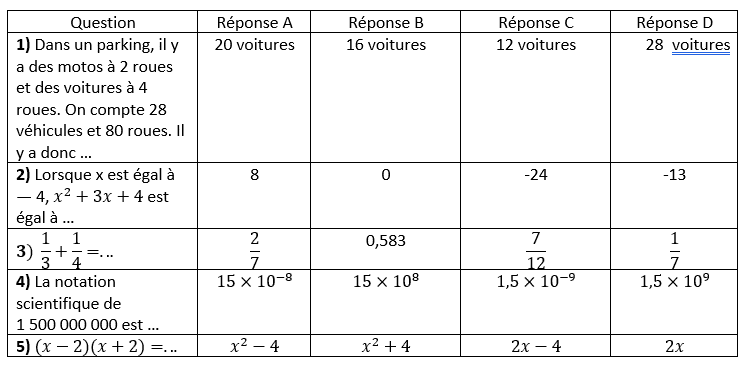
Exercice n° 1 : 5 points.

Cet exercice est un questionnaire à choix multiple (QCM).

Pour chacune des cinq questions, quatre réponses sont proposées, une seule d’entre elles est exacte.

Pour chacune des cinq questions, indiquer sur la copie le numéro de la question et la réponse choisie.

On rappelle que toute réponse doit être justifiée.

Une réponse fausse ou l’absence de réponse ne retire pas de point.

Exercice n° 2 : 6 points.

Donner la décomposition en facteurs premiers des nombres entiers 108 et 225.
En utilisant les décompositions en facteurs premiers précédentes, rendre la fraction $\frac{108}{225}$ irréductible.
Carole souhaite réaliser une mosaïque sur un mur de sa maison. La surface à paver est un rectangle de dimensions 108 cm et 225 cm et doit être entièrement recouverte par des carreaux de faïence carrés de même dimension sans découpe.

Carole peut-elle utiliser des carreaux de 3 cm de côté ? De 6 cm de côté ?

4 . Quelle est la dimension maximale des carreaux que Carole peut poser ? Combien de carreaux utilisera-t-elle ?

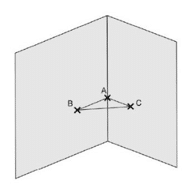
Exercice n°3 : 4 points.

Des élèves ont tendu deux cordes entre les points A et D, puis entre les points B et C. Les deux cordes se coupent en E.

On sait que : EA=7 m, EB = 13 m, EC= 10 m et ED = 9 m.

Les droites (AC) et (BD) sont-elles parallèles ?

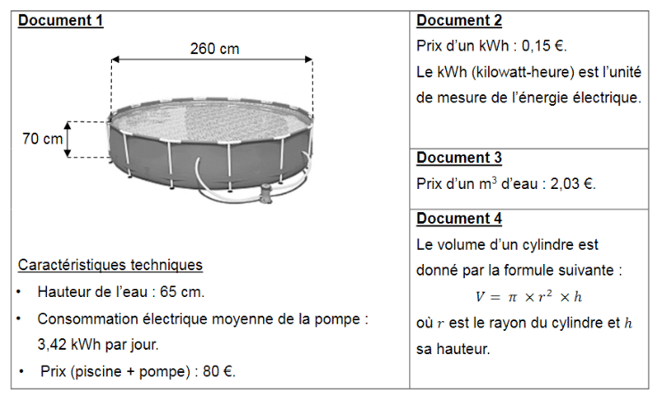
Exercice n° 4 : 7 points.

Une famille désire acheter, pour les enfants, une piscine cylindrique hors sol équipée d’une pompe électrique. Elle compte l’utiliser cet été du mois de juin au mois de septembre inclus.

Elle dispose d’un budget de 200 €.

A l’aide des documents suivants, dire si le budget de cette famille est suffisant pour l’achat de cette piscine et les frais de fonctionnement.

Laisser toute trace de recherche, même si elle n’est pas aboutie.

Exercice n° 5 : 4 points.

Claude, un menuisier, prend les mesures suivantes dans le coin d’un mur à 1 mètre au-dessus du sol pour construire une étagère ABC :

AB = 65 cm ; AC = 72 cm et BC = 97 cm

Il réfléchit quelques minutes et assure que l’étagère a un angle droit.

A-t-il raison ? Justifier votre réponse.

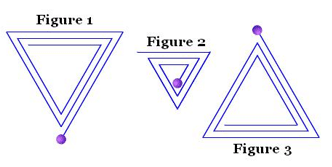
Exercice n° 6 : 3 points.

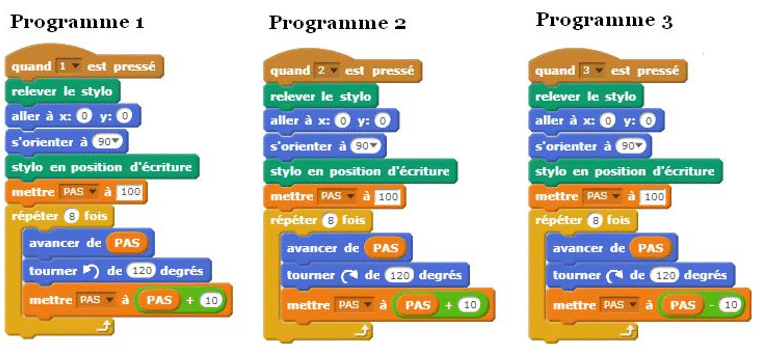
Voici trois figures réalisées avec le logiciel Scratch.

Associez chaque figure à son programme correspondant (justifier vos réponses).

Exercice n° 7 : 7 points

On considère le programme de calcul suivant :

Montrer que si le nombre choisi au départ est 2, alors le résultat obtenu est 5.
Quel est le résultat obtenu avec ce programme si le nombre choisi au départ est −10 ?
Un élève s’aperçoit qu’en calculant le double de 2 et en ajoutant 1, il obtient 5, le même résultat que celui qu’il a obtenu à la question 1.

Il pense alors que le programme de calcul revient à calculer le double du nombre de départ et à ajouter 1.

A-t-il raison ?

Si désigne le nombre choisi au départ, montrer que le résultat du programme de calcul est .

5.Quel(s) nombre(s) doit-on choisir au départ du programme de calcul pour obtenir 17 comme résultat ?

Exercice n° 8 : 3 points.

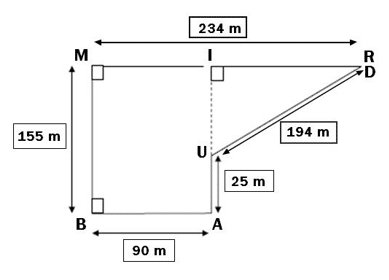
Voici le parcours du cross du collège Arthur Rimbaud schématisé par la figure RIMBAUD ci-dessous :

Les élèves de troisième doivent effectuer quatre tours de parcours. Calculer la longueur totale de leur course.

Tery, le vainqueur de la course des garçons de troisième a effectué sa course en 10 minutes et 42 secondes.

Calculer sa vitesse en m/s (arrondir le résultat au centième).

Si Tery maintenait sa vitesse moyenne, pensez-vous qu’il pourrait battre le champion Georges Richmond qui a gagné la course sur 15 km des Foulées du Front de mer en 55 minutes et 11 secondes ?

Consulter le corrigé en ligne

3.9/5 - (7 votes)

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet Maths 2021 : sujet et corrigé du brevet blanc de maths» au format PDF.

D'autres cours et exercices à consulter

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.

D'autres cours et exercices à consulter

Laisser un commentaire