Antilles et Guyane 2019 : brevet de maths avec sujet et corrigé en PDF
Exercice 1 : 13 points
Damien a fabriqué trois dés à six faces parfaitement équilibrés mais un peu particuliers.
Sur les faces du premier dé sont écrits les six plus petits nombres pairs strictement positifs : 2; 4; 6;
8; 10; 12.
Sur les faces du deuxième dé sont écrits les six plus petits nombres impairs positifs.
Sur les faces du troisième dé sont écrits les six plus petits nombres premiers.
Après avoir lancé un dé, on note le nombre obtenu sur la face du dessus.
1. Quels sont les six nombres figurant sur le deuxième dé?
Quels sont les six nombres figurant sur le troisième dé?
2. Zoé choisit le troisième dé et le lance. Elle met au carré le nombre obtenu. Léo choisit le premier
dé et le lance. Il met au carré le nombre obtenu.
a. Zoé a obtenu un carré égal à 25. Quel était le nombre lu sur le dé qu’elle a lancé?
b. Quelle est la probabilité que Léo obtienne un carré supérieur à celui obtenu par Zoé?
3. Mohamed choisit un des trois dés et le lance quatre fois de suite. Il multiplie les quatre nombres
obtenus et obtient 525.
a. Peut-on déterminer les nombres obtenus lors des quatre lancers ? Justifier.
b. Peut-on déterminer quel est le dé choisi par Mohamed? Justifier.
Exercice 2 : 18 points
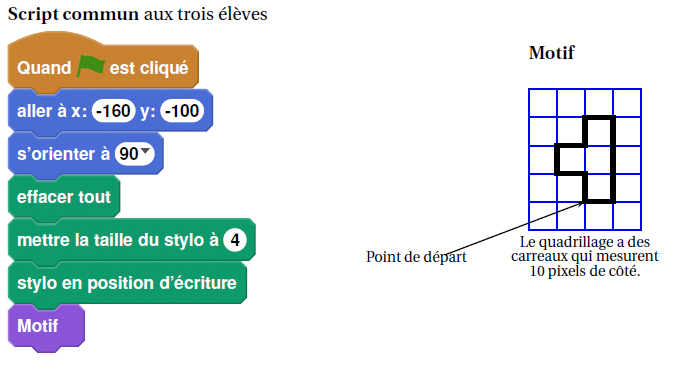
« S’orienter à 90 » signifie que l’on se tourne vers la droite.
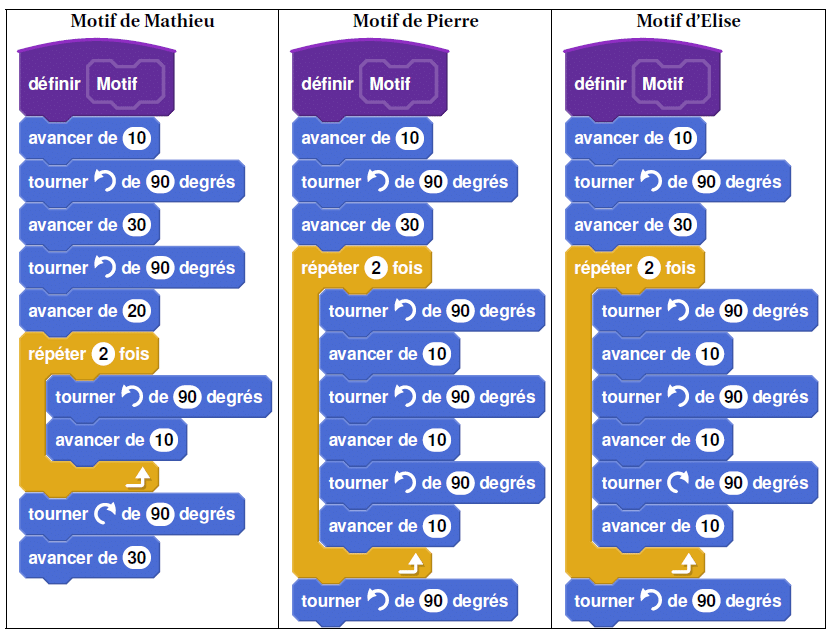
Mathieu, Pierre et Elise souhaitent tracer le motif ci-dessous à l’aide de leur ordinateur. Ils commencent
tous par le script commun ci-dessous, mais écrivent un script Motif différent.
1. Tracer le motif de Mathieu en prenant comme échelle : 1 cm pour 10 pixels.
2. Quel élève a un script permettant d’obtenir le motif souhaité? On ne demande pas de justifier.
3. a. On utilise ce motif pour obtenir la figure ci-dessous.

Quelle transformation du plan permet de passer à la fois du motif 1 au motif 2, du motif 2 au motif 3 et du motif 3 au motif 4?
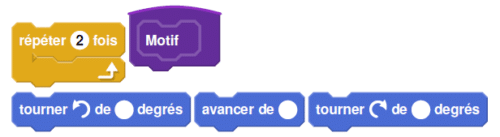
b. Modifier le script commun à partir de la ligne 7 incluse pour obtenir la figure voulue.
On écrira sur la copie uniquement la partie modifiée.
Vous pourrez utiliser certaines ou toutes les instructions suivantes :
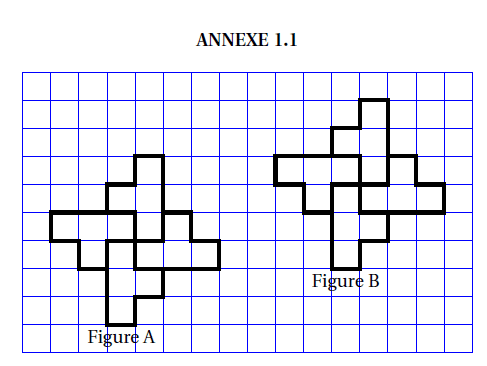
4. Un élève trace les deux figures A et B que vous trouverez en ANNEXE 1.1
Placer sur cette annexe, qui est à rendre avec la copie, le centre O de la symétrie centrale qui
transforme la figure A en figure B.
Exercice 3 : 17 points
Le premier juillet 2018, la vitesse maximale autorisée sur les routes à double sens de circulation, sans
séparateur central, a été abaissée de 90 km/h à 80 km/h.
En 2016, 1 911 personnes ont été tuées sur les routes à double sens de circulation, sans séparateur
central, ce qui représente environ 55% des décès sur l’ensemble des routes en France.
Source : www.securite-routiere.gouv.fr
1. a. Montrer qu’en 2016, il Y a eu environ 3475 décès sur l’ensemble des routes en France.
b. Des experts ont estimé que la baisse de la vitesse à 80 km/h aurait permis de sauver 400
vies en 2016.
De quel pourcentage le nombre de morts sur l’ensemble des routes de France aurait-il
baissé? Donner une valeur approchée à 0,1% près.
2. En septembre 2018, des gendarmes ont effectué une série de contrôles sur une route dont la
vitesse maximale autorisée est 80 km/h. Les résultats ont été entrés dans un tableur dans l’ordre
croissant des vitesses. Malheureusement, les données de la colonne B ont été effacées.
a. Calculer la moyenne des vitesses des automobilistes contrôlés qui ont dépassé la vitesse
maximale autorisée. Donner une valeur approchée à 0,1 km/h près.
b. Sachant que l’étendue des vitesses relevées est égale à 27 km/h et que la médiane est égale
à 82 km/h, quelles sont les données manquantes dans la colonne B?
c. Quelle formule doit-on saisir dans la cellule K2 pour obtenir le nombre total d’automobilistes
contrôlés ?
Exercice 4 : 10 points
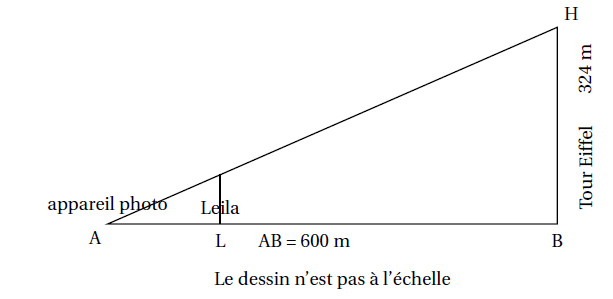
Leila est en visite à Paris. Aujourd’hui, elle est au Champ de Mars où l’on peut voir la tour Eiffel dont
la hauteur totale BH est 324 m.
Elle pose son appareil photo au sol à une distance AB = 600 m du monument et le programme pour
prendre une photo (voir le dessin ci-dessous).
1. Quelle est la mesure, au degré près, de l’angle ?
2. Sachant que Leila mesure 1,70 m, à quelle distance AL de son appareil doit-elle se placer pour
paraître aussi grande que la tour Eiffel sur sa photo?
Donner une valeur approchée du résultat au centimètre près.
Exercice 5 : 22 points
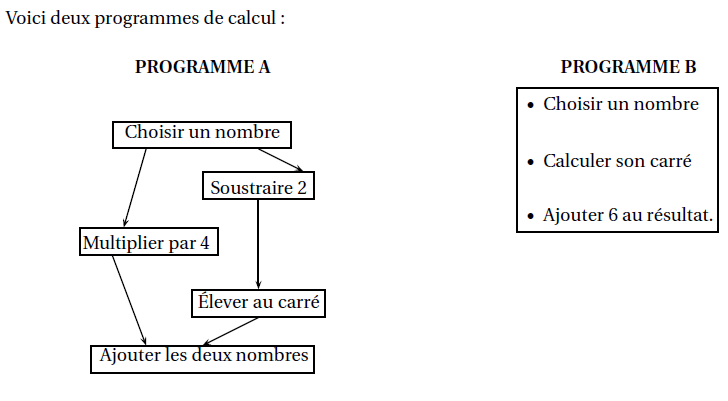
1. a. Montrer que, si l’on choisit le nombre 5, le résultat du programme A est 29.
b. Quel est le résultat du programme B si on choisit le nombre 5?
c. Si on nomme x le nombre choisi, expliquer pourquoi le résultat du programme A peut
s’écrire x² +4.
2. Quel est le résultat du programme B si l’on nomme x le nombre choisi ?
3. Les affirmations suivantes sont-elles vraies ou fausses ? Justifier les réponses et écrire les étapes
des éventuels calculs :
a. « Si l’on choisit le nombre , le résultat du programme B est
. »
b. « Si l’on choisit un nombre entier, le résultat du programme B est un nombre entier impair.
»
c. « Le résultat du programme B est toujours un nombre positif. »
d. « Pour un même nombre entier choisi, les résultats des programmes A et B sont ou bien
tous les deux des entiers pairs, ou bien tous les deux des entiers impairs. »
Exercice 6 : 20 points
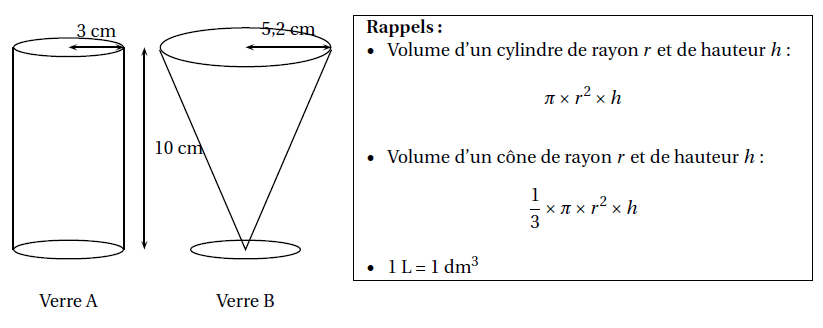
Pour servir ses jus de fruits, un restaurateur a le choix entre deux types de verres : un verre cylindrique
A de hauteur 10 cm et de rayon 3 cm et un verre conique B de hauteur 10 cm et de rayon 5,2 cm.
Le graphique ANNEXE 1.2 représente le volume de jus de fruits dans chacun des verres en
fonction de la hauteur de jus de fruits qu’ils contiennent.
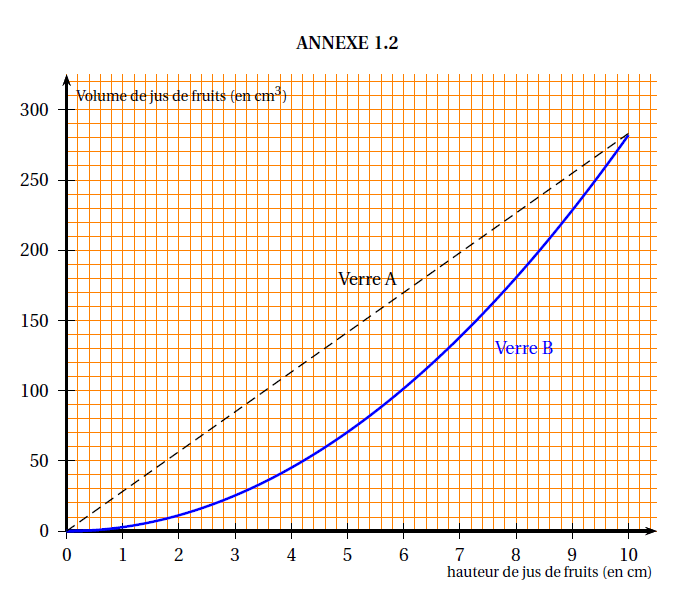
1. Répondre aux questions suivantes à l’aide du graphique en ANNEXE 1.2 :
a. Pour quel verre le volume et la hauteur de jus de fruits sont-ils proportionnels ? Justifier.
b. Pour le verre A, quel est le volume de jus de fruits si la hauteur est de 5 cm?
c. Quelle est la hauteur de jus de fruits si on en verse 50 dans le verre B?
2. Montrer, par le calcul, que les deux verres ont le même volume total à 1 près.
3. Calculer la hauteur du jus de fruits servi dans le verre A pour que le volume de jus soit égal à
200 . Donner une valeur approchée au centimètre près.
4. Un restaurateur sert ses verres de telle sorte que la hauteur du jus de fruits dans le verre soit
égale à 8 cm.
a. Par lecture graphique, déterminer quel type de verre le restaurateur doit choisir pour servir
le plus grand nombre possible de verres avec 1 L de jus de fruits.
b. Par le calcul, déterminer le nombre maximum de verres A qu’il pourra servir avec 1 L de
jus de fruits.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «antilles et Guyane 2019 : brevet de maths avec sujet et corrigé en PDF» au format PDF.
D'autres cours et exercices à consulter
- Polynésie Française : brevet de maths 2022 avec sujet et corrigé
- Brevet de maths 2024 aux centres étrangers avec sujet et corrigé.
- Asie et Pacifique : brevet de maths 2022 avec sujet et corrigé
- Brevet Maths 2021 : sujet et corrigé du brevet blanc de maths
- Brevet Maths 2021 : sujet corrigé blanc pour la révision du DNB
- Brevet Maths 2021 : sujet blanc pour réviser le brevet
- Brevet de maths 2022 aux centres étrangers : sujet et corrigé du brevet.
- Brevet de maths 2017 : sujet blanc