Statistiques : exercices de maths en 4ème corrigés en PDF.

Mis à jour le 28 mai 2025

Sommaire

✏️Exercices

4ème • Collège

Statistiques

⏱️ Temps de travail : 20-45 min

🎯 Niveau : Collège

📱 Format : Gratuit

📄 PDF : Disponible

Les statistiques avec des exercices de maths en 4ème sur corrigés en PDF. Calculer la moyenne et la médiane d’une série statistiques. Connaître la formule de la fréquence et savoir représenter des diagrammes en bâtons et circulaires ainsi que des histogrammes.

Exercice 1 – Statistiques et caractère continu

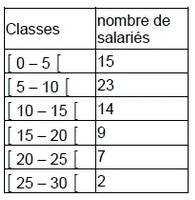
Dans une entreprise de 70 personnes, l’ancienneté des salariés se décompose comme suit :

1. Que signifie l’ écriture [ 15 — 20 [ ?
2. Calculer les effectifs cumulés croissants et les effectifs cumulés décroissants.
3. Combien de personnes ont plus de 10 ans d’ancienneté ? Combien de personnes ont
moins de 20 ans d’ ancienneté ?
4. Représenter le polygone des effectifs cumulés croissants.
5. En remplaçant chaque classe par son centre, calculer l’ancienneté moyenne de
l’ entreprise.
6. Calculer les fréquences de chaque valeur ainsi que les fréquences cumulées.
7. Quel est le pourcentage de salariés dont l’ancienneté est comprise entre 5 et 15 ans ?

Exercice 2 – Utilisation du vocabulaire

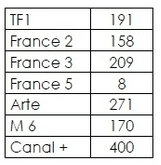
Le tableau suivant donne le nombre de films diffusés à la télévision en 2004 par les principales
grandes chaines françaises.

l. Donner la population étudiée et le caractère étudié.
2. Que signifie le chiffre 271 à la ligne Arte ?
3. Calculer l’effectif total.
4. Donner la fréquence relative à chaque chaîne.
5. Présenter les résultats sous forme d’un diagramme circulaire.

Exercice 3 – Calculer une moyenne

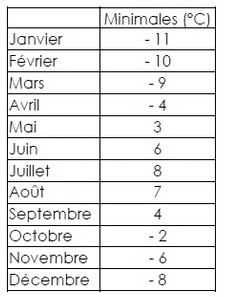
Le tableau ci-dessous donne les températures minimales moyennes relevées Narssak au
Groënland.
Calculer la moyenne annuelle de cette série.

Exercice 4 – Exploitation d’un histogramme

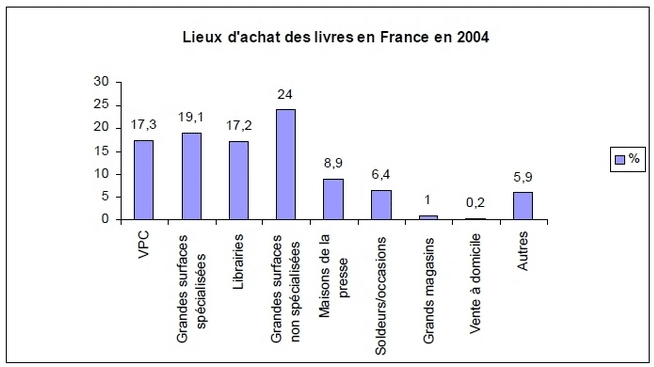
L’histogramme ci-dessous donne les lieux où la population française a acheté ses livres en 2004.

l. Quelle est la population étudiée ? Quel est le critère étudié ?
2. Quelles sont les données représentées sur le graphique?
3. Que signifie le chiffre 17,2 dans la colonne librairies ?
4. Sous quelle autre forme graphique aurait-il été opportun de représenter cette série ?

Exercice 5 :

Le tableau ci-dessous présente le nombre d’opérations quotidiennes réalisées dans une clinique
vétérinaire durant le mois de janvier.

a. Déterminer la médiane de cette série.
b. Interpréter le résultat pour cette situation.

Exercice 6 :

Un éleveur de chèvres fabrique de délicieux tourteaux fromagers.
Voici la répartition des masses de 80 de ces tourteaux.

a. Déterminer la médiane de cette série.
b. Recopier et compléter : « Au moins 50 % de ces tourteaux ont une masse comprise entre … et … ».
Déterminer exactement le pourcentage de tourteaux dont la masse est :
• inférieure ou égale à la médiane,
• supérieure ou égale à la médiane.

Exercice 7 :

Voici une série de nombres :

Mathis : « La moyenne est 12, c’est la valeur du milieu. »
Maeva : « Pas du tout ! 12 est la médiane de la série car il y a trois nombres avant et trois nombres
après. »
Que peut-on penser de leurs affirmations ?

Exercice 8 :

Parmi les séries ci-dessous, quelles sont celles qui ont la même médiane ?

Quelle est cette médiane ?

Exercice 9 :

Voici la répartition de certains élèves d’un collège selon le bus scolaire qu’ils utilisent pour s’y rendre.

Quel est le nombre moyen d’élèves par bus ?

Exercice 10 :

Voici les dix meilleures performances réalisées par Mélina Robert-Michon au lancer de
disque de juin à août.
63,09m 63,23 m 65,04m 62,77 m 62,24 m
61,81 m 63,78m 62,57 m 62,39m 61,78 m
a. Calculer la moyenne de ces performances.
b. Supprimer les deux performances extrêmes et calculer la moyenne des huit autres valeurs.
c. La moyenne des valeurs d’une série est-elle sensible aux valeurs extrêmes de la série ?

Exercice 11 :

Le tableau ci-dessous présente la répartition de la population en région Centre-Val de Loire au
1er janvier 2014.

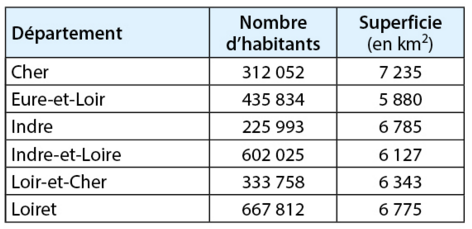
1. Pour chaque département, calculer le nombre moyen d’habitants par km².
Donner une valeur approchée à l’unité près.
2. a. Calculer le nombre d’habitants et la superficie de la région Centre-Val de Loire.
b. En déduire le nombre moyen d’habitants par km² de cette région.
Donner une valeur approchée à l’unité près.
3. Calculer la moyenne des moyennes obtenues à la question 1. Que remarque-t-on ? Expliquer.

Exercice 12 :

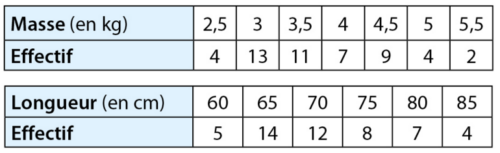
Pour étudier les saumons qui remontent le Scorff, rivière du Morbihan,
on a capturé 50 saumons et on les a pesés et mesurés avant de les relâcher.

Calculer, pour ces saumons :
a. leur masse moyenne, en kg;
b. leur longueur moyenne, en cm.

Exercice 13 :

Un apiculteur a relevé les masses de miel récolté dans ses deux ruchers.

Déterminer la masse médiane de miel récolté dans chacun de ces deux ruchers.

Exercice 14 :

Cette feuille de calcul présente la consommation de fromage par kilogramme et par
habitant dans plusieurs pays d’Europe.

a. Réaliser cette feuille de calcul et calculer la moyenne de la Série en Cellule .
Interpréter le résultat obtenu.
b. Quelle formule saisit-on en cellule pour déterminer la médiane de cette série ?
Interpréter le résultat obtenu.
c. Ôter maintenant les deux valeurs extrêmes : 4,3 (Ukraine) et 26,7 (France).
Observer les affichages en et et commenter.

Exercice 15 :

Yann note les distances qu’il parcourt chaque jour d’une semaine lors de ses randonnées.
Quelle peut être la distance parcourue par Yann lors de sa randonnée du dimanche
si la médiane de la série des sept distances est (en km) :

a. 7,5 ? b. 7 ?
C. 6,5 ? d. 5 ?
Donner toutes les réponses possibles, ou, si ce n’est pas possible, expliquer pourquoi.

Exercice 16 :

Un enquêteur a noté le nombre d’appareils ménagers que possède chacune des familles d’un immeuble :

4	9	4	5	5	4	5	5	7	8	5	4	6	6	3
8	8	3	5	6	7	8	4	5	5	4	6	7	5	9

1°) Dans cette série statistique, quel est l’effectif de la valeur 4 ?

2°) Quel est l’effectif total ?

3°) Représente la série sous forme de tableau.

Exercice 17 :

Voici une approximation du nombre $\pi$

3,141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 820 9.

1°) Quel est l’effectif du chiffre 0 ?

2°) Remplis un tableau donnant l’effectif de chaque chiffre après la virgule.

Exercice 18 :

Les 24 élèves d’une classe de 5ème ont élu leur délégué. Le dépouillement des bulletins a donné les résultats suivants :

éric – éric – Chloé – éric – Chloé – Anne – Chloé – éric – Yann – Yann – éric – Lise – éric – Chloé – Chloé – Yann – Lise – éric – éric – Yann – Chloé – Chloé – éric – Yann.

1°) Présente ces données dans un tableau.

2°) Quel est l’effectif maximum ?

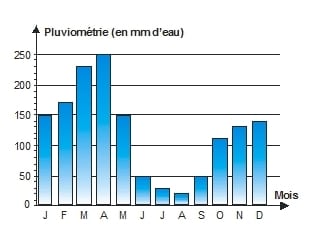
Exercice 19 : « Pluviométrie d’une ville »

1°) Quels sont les 4 mois de sécheresse ?

2°) La ville a subi 2 mois d’inondations : lesquels ?

3°) Indique les pluviométries maximum et minimum.

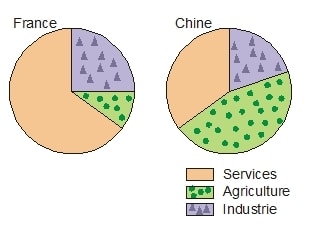
Exercice 20 : « Répartition de la population active »

1°) Quel est le secteur le plus important dans chaque pays ?

2°) Dans quel pays l’industrie a-t-elle le plus d’importance ?

Exercice 21 :

Les activités artistiques pratiquées par les Français se répartissent ainsi : la photo : 46% ; la vidéo avec 21 % ; le dessin avec 13 %, puis la danse et le piano avec 10 % chacun.

Construis un diagramme circulaire des activités artistiques des Français.

Exercice 22 :

Yannick a 45 albums de BD : 15 Tintin ; 6 Batman ; 10 Titeuf et 14 Bone.

Représente cette répartition à l’aide d’un diagramme circulaire.

Exercice 23 :

Une enquête, réalisée sur 30 enfants, porte sur le temps t , en heures, passé devant la télévision.

La répartition est donnée dans le tableau suivant :

Temps t ( en h )	0 $\leq\,$ t < 0,5	0,5 $\leq\,$ t < 1	1 $\leq\,$ t < 1,5	1,5 $\leq\,$ t < 2
Nombre d’enfants	12	9	6	3

1°) Combien d’enfants regardent la télé plus de 1 h ? moins d’une demi-heure ?

2°) Représente ces données par un histogramme.

Exercice 24 :

Voici le nombre des sélections en équipe de France des footballeurs qui ont participé à la coupe d’Europe 2000.

38 ; 43 ; 2 ; 74 ; 28 ; 72 ; 30 ; 58 ; 62 ; 67 ; 44 ; 37 ; 41 ; 30 ; 59 ; 17 ; 43 ; 21 ; 38 ; 21 ; 18.

1°) Reproduis et complète le tableau suivant :

Nombre n de sélections	n < 25	25 $\leq\,$ n < 50	50 $\leq\,$ n < 75
Nombre de joueurs

2°) Représente ces données par un histogramme.

Exercice 25 :

Ecrire dans un tableau les effectifs et les fréquences de chacune des notes rencontrées dans la phrase musicale ci-dessous.

Exercice 26 :

Quentin a lancé 20 fois un dé. Voici les résultats des lancers :

5 ; 6 ; 4 ; 5 ; 3 ; 5 ; 6 ; 1 ; 2 ; 3 ; 5 ; 6 ; 4 ;

5 ; 1 ; 2 ; 5 ; 6 ; 1 ; 2

1°) Calcule la fréquence du résultat « 5 ».

2°) Calcule la fréquence du résultat « 6 ».

Exercice 27 :

Recopier et compléter ce tableau qui présente le nombre de visiteurs sur un site archéologique.

Exercice 28 :

Lors des Jeux olympiques de la jeunesse, à Nankin (en Chine), la France a obtenu
20 médailles. Voici leur répartition.

a. Recopier et compléter le tableau.
b. Fatou a-t-elle raison ? Expliquer.

Exercice 29 :

Voici les résultats d’une enquête auprès des 800 élèves d’un collège sur leur fréquentation du
restaurant scolaire par semaine.

a. Recopier et compléter ce tableau.
b. Tom a-t-il raison ? Expliquer.

Exercice 30 :
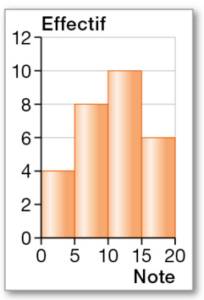
Un professeur présente la répartition des notes (n) à une évaluation sous la forme
de cet histogramme.
1. Quelle est l’amplitude de chaque classe ?
2. On s’intéresse à la classe $5\,\leq\,\,n\,<\,10$ .
a. Citer cinq notes possibles de cette classe.
b. Quel est l’effectif de cette classe ?
3. Lire en complétant : « … notes sont comprises entre 10 (…) et 15 (…) ».
4.Combien de notes sont supérieures ou égales à 10 ?
5. Calculer le nombre total de notes.

Exercice 31 :

Un enseignant a demandé à ses élèves de cinquième le moyen de transport qu’ils utilisent pour

venir au collège.

Il présente les résultats dans le tableau suivant :

Quelle est la population étudiée ?
Quel est le caractère étudié? Est-il quantitatif ou qualitatif ?
Quel est l’effectif de la valeur « bus »?
Quel est l’effectif total de la population étudiée ?Que représente ce nombre ?

Exercice 32 :

Le tableau suivant donne le nombre de membres par catégorie dans un club de basket.

1.Représenter les données de ce tableau à l’aide d’un diagramme circulaire. Pour cela, reproduire

et compléter le tableau suivant :

2.Que peut-on dire de la répartition des membres de ce club par catégorie ?

Exercice 33 :

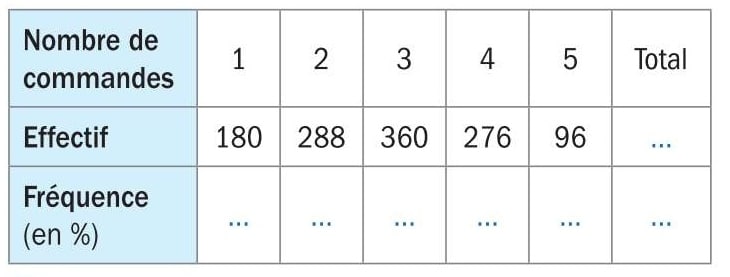
Pendant un an, un site internet de vente de chaussures de sport enregistre

le nombre de commandes de ses clients.

1.Reproduire et compléter le tableau suivant :

2.Quel est le pourcentage de clients qui ont effectué dans l’année :

a. au moins deux commandes;

b. moins de trois commandes.

3. Est-il vrai que plus du tiers des clients de ce site ont effectué au moins quatre commandes dans l’année? Justifier.

Exercice 34 :

On a interrogé plusieurs familles pour connaitre le nombre de téléphones portables

qu’elles possèdent.

Le tableau suivant regroupe leurs réponses :

Quel est le nombre moyen de téléphones portable par famille ?

Exercice 35 :

Pour soutenir une organisation humanitaire, un collège organise une courses d’endurance.

Le tableau suivant donne les distances parcourues par les élèves.

1.Calculer, en arrondissant au dixième, la distance moyenne parcourue par un élève.

2.Les 75 adultes ont parcouru en moyenne 8,2 km chacun.

L’an passé, la distance totale parcourue par tous était de 2 650 km.

Le collège avait pour objectif de faire 10% de mieux.

Cet objectif est-il réalisé?

Exercice 36 :

Le tableau ci-dessous présente le nombre d’opérations quotidiennes réalisées dans une clinique
vétérinaire durant le mois de janvier.

a. Déterminer la médiane de cette Série.
b. Interpréter le résultat pour cette situation.

Exercice 37 :

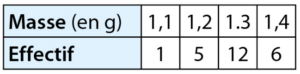
Un éleveur de chèvres fabrique de délicieux tourteaux fromagers.
Voici la répartition des masses de 80 de ces tourteaux.

a. Déterminer la médiane de cette série.
b. Recopier et compléter : « Au moins 50 % de ces tourteaux ont une masse comprise entre … et … »..
c. Déterminer exactement le pourcentage de tourteaux dont la masse est :
• inférieure ou égale à la médiane,
• supérieure ou égale à la médiane.

Exercice 38 :

Voici la répartition d’un modèle de T-shirt selon la taille, dans un magasin.

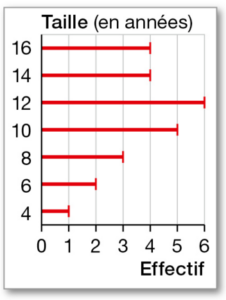
a. Déterminer la taille médiane de ces T-shirts.
b. Axel affirme : « La moitié des T-shirts sont de taille 12 ans au moins. »
A-t-il raison ? Expliquer.

c. Déterminer le pourcentage de T-shirts de taille :
• inférieure ou égale à la médiane,
• supérieure ou égale à la médiane.

Exercice 39 :

Indiquer qui, de Virgile ou de Louise, a eu la meilleure moyenne en technologie au premier
trimestre.
Notes de Virgile: 16; 11 ; 9; 14
Notes de Louise : 13,5 ; 9,5 ; 13; 12

Exercice 40 :

Dans un immeuble, on a relevé le nombre de personnes par appartement.

Calculer :
a. l’effectif total des personnes de cet immeuble ;
b. le nombre moyen de personnes par appartement.

Exercice 41 :

Dans chaque cas, déterminer la médiane de la série.

Préciser si elle est une valeur de la série.

$a.\,68;69;70;73;75\\b.\,3;5;5;7;7;7;8\\c.\,13;13;15;15;16;18;19;20$

Exercice 42 :

Voici une série de nombres :

Exercice 43 :

On a relevé des températures (en °C) pendant huit jours :
Quentin affirme : « La moyenne et la médiane de ces températures sont égales ».
Est-ce exact ? Expliquer.

Exercice 44 :

Voici les dix meilleures performances réalisées par Mélina Robert-Michon au lancer de
disque.
63,09m 63,23m 65,04m 62,77m 62,24 m
61,81m 63,78m 62,57m 62,39m 61,78m

a. Calculer la moyenne de ces performances.
b. Supprimer les deux performances extrêmes et calculer la moyenne des huit autres valeurs.
c. La moyenne des valeurs d’une série est-elle sensible aux valeurs extrêmes de la série ?

Exercice 45 :

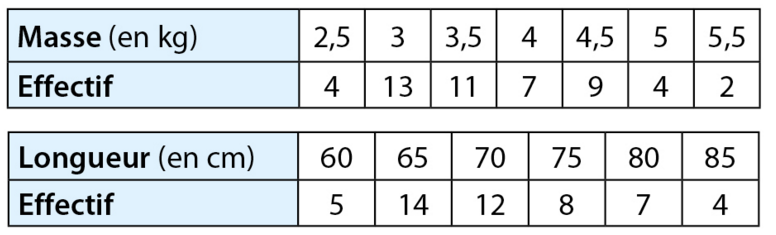
Pour étudier les saumons qui remontent le Scorff, rivière du Morbihan, on a capturé 50 saumons et
on les a pesés et mesurés avant de les relâcher.

Calculer, pour ces saumons :
a. leur masse moyenne, en kg ;
b. leur longueur moyenne, en cm.

Exercice 46 :

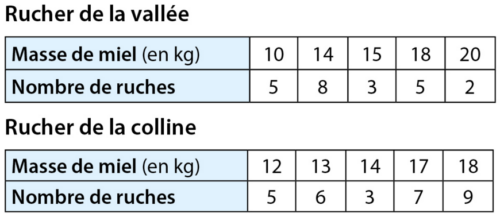
Un apiculteur a relevé les masses de miel récolté dans ses deux ruchers.
Rucher de la vallée

Rucher de la colline

Déterminer la masse médiane de miel récolté dans chacun de ces deux ruchers.

Exercice 47 :

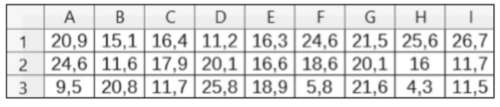
Cette feuille de calcul présente la consommation de fromage par kilogramme et par
habitant dans plusieurs pays d’Europe.

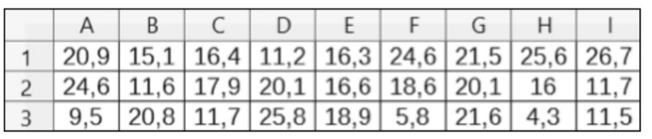
a. Réaliser cette feuille de calcul et calculer la moyenne de la série en cellule K1.
Interpréter le résultat obtenu.
b. Quelle formule saisit-on en cellule K2 pour déterminer la médiane de cette série ?
Interpréter le résultat obtenu.
c. Ôter maintenant les deux valeurs extrêmes : 4,3 (Ukraine) et 26,7 (France).
Observer les affichages en K1 et K2 et commenter.

Exercice 48 :

Ce diagramme donne les tailles à la naissance de bébés nés dans une maternité en une semaine.

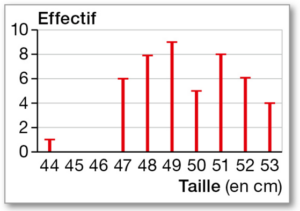
a. Calculer l’étendue de la série.

b. Selon les spécialistes, la taille à la naissance des bébés non prématurés est comprise entre 46 cm et
54 cm, avec une moyenne d’environ 50 cm.
Est-ce le cas ici ?

Exercice 49 :

Lors d’un TP de physique, des élèves ont déterminé la masse d’un litre d’air.

Quelle est l’étendue de la série des résultats ?
Que représente-t-elle ?

Exercice 50 :

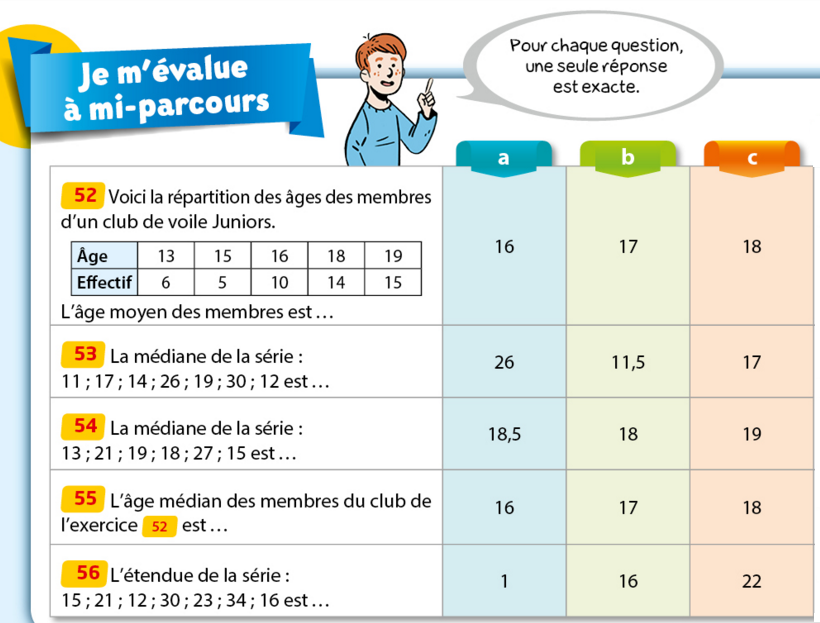
Répondre au QCM sur les statistiques suivant :

4.4/5 - (20115 votes)

×12

L’équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs

200+ Années cumulées

Quotidien Mise à jour

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «statistiques : exercices de maths en 4ème corrigés en PDF.» au format PDF.