Translation et rotation : cours de maths en 4ème en PDF.

Sommaire

La translation et la rotation dans un cours de maths en 4ème au cycle 4.Nous étudierons la définition et les propriétés de ces deux transformations du plan.Les propriétés de conservation de l’alignement, des longueurs, des aires, des milieux et des mesures d’angles dans cette leçon destinées aux élèves de quatrième.

I. La translation

Définition

Définition :

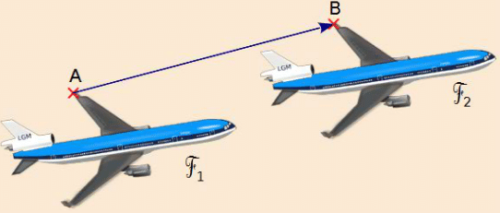
Lorsque l’on fait glisser la figure F_1 sans la faire tourner, de manière à ce que A arrive en B,elle se superpose avec la figure F_2 .

On dit que la figure F_2 est l’image de la figure F_1 par la translation qui transforme A en B.

2. Image d’un point et d’un segment

Propriété n° 1 :

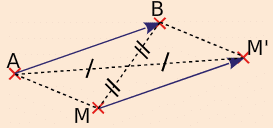
L’image du point M, par la translation qui transforme A en B, est le point M’ tel queles segments [MB] et [AM’] ont le même milieu.

Si les points ne sont pas alignés alors ABM’M est un parallélogramme.

Propriété n° 2 :

L’image d’un segment par une translation est un segment qui lui est parallèle et de même longueur.

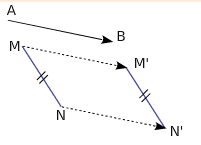
Exemple :

Dans la translation qui transforme A en B, le segment [MN] a pour image le segment [M’N’].

Donc les segments [MN] et [M’N’] sont parallèles et de même longueur.

II. La rotation

Définition

Définition :

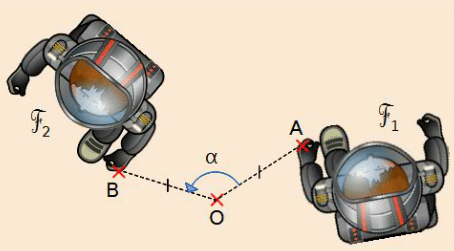
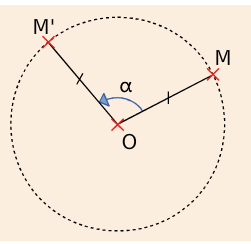
Lorsque l’on fait tourner la figure F_1 autour du point O, d’un angle de mesure $\alpha$ , dans le sens contraire des aiguilles d’une montre, elle se superpose avec la figure F_2 .On dit que la figure F_2 est l’image de la figure F_1 par la rotation de centre O et d’angle $\alpha$ .

Remarque :

$\star\,$ Dans tout ce chapitre, le sens de rotation sera toujours le sens trigonométrique (sens contraire du déplacement des aiguilles d’une montre).

$\star\,$ La rotation de centre O et d’angle 180° est la symétrie centrale de centre O.

2. Image d’un point

Propriété :

On considère O et M deux points distincts.

L’image du point M par la rotation de centre O et d’angle $\alpha$ est le point M’ tel que :

OM'=OM et $\widehat{MOM'}=\alpha$ .

III. Les propriétés de la translation et de la rotation

Propriété :

La translation et la rotation conservent les longueurs, l’alignement, les aires, les milieux et les mesures d’angle.

Exemple :

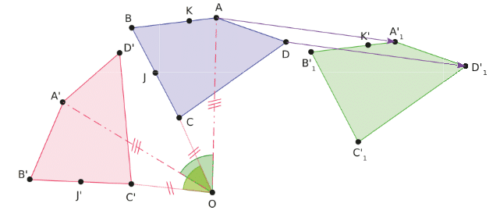
Le quadrilatère A’B’C’D’ est l’image de ABCD par la rotation de centre O et d’angle 60°.

Le quadrilatère est l’image de ABCD par la translation qui transforme en .

$\star\,$ Les aires et les périmètres des trois quadrilatères sont égaux..

$\star\,$ Les points A,B,K sont alignés donc leurs images sont également alignées.

$\star\,$ Le point J est le milieu du segment [BC] donc son image J’ par la rotation est le milieu du segment [B’C’].

$\star\,$ L’angle $\widehat{A'_1B'_1C'_1}$ est l’image de l’angle $\widehat{ABC}$ par la translation, ils ont donc la même mesure.

$\star\,$ L’angle $\widehat{A'B'C'}$ est l’image de l’angle $\widehat{ABC}$ par la translation, ils ont donc la même mesure.

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «translation et rotation : cours de maths en 4ème en PDF.» au format PDF.

D'autres cours et exercices à consulter

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.