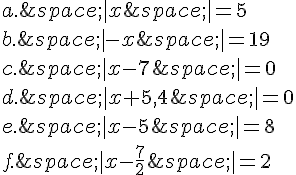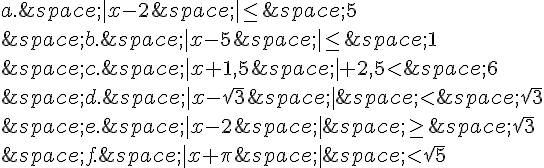Tous les exercices de maths en 2de pour les élèves de seconde.

Exercice 1 :

Résoudre dans les équations et inéquations suivantes :

a) | 2 – x | < 4

b) | 6 – 2 x | = 3

c) | x + 2 | > 3

d) | x + 2 | < | x + 3 |

e) | x³ – 1 | + p > 0

f) 3 < | x + 2 | < 4

g) | 4 x² – 12 x + 9 | = 4

h) | 3 x + 1 | + | 1 – x | > 3

i) | 1 + x² | = 2x

Exercice 2 :

Calculer.

a) b) c) $|-\frac{100}{3}|$

d) e) $|\sqrt{17}-2|$ f) $|2-\sqrt{17}|$

Exercice 3 :

Sans calculatrice, simplifier :

a) b)

c) $\frac{|5-8|-3}{2}$ d)

Exercice 4 :

1.a) Sur une droite graduée, placer les nombres 5 et $\frac{1}{3}$ .

b) Calculer la distance entre 5 et $\frac{1}{3}$ .

2. Reprendre la question 1. avec 3 et $-\frac{4}{5}$ .

3. Reprendre la question 1. avec -1 et $-\frac{4}{5}$ .

Exercice 5 :

A l’aide d’une valeur absolue, écrire la distance entre :

a) $\frac{125}{3}$ et 2. b) $\sqrt{2}$ et 5

c) – 5 et $\frac{12}{5}$ d) $\pi$ et 4

Exercice 6 :

sans calculatrice, simplifier :

a) $|5-\pi|$ b) $|8-\frac{2}{3}|$ c) $|2-\frac{9}{2}|$

d) e) $|-5-\pi|$ f) $|\frac{1}{2}+6|$

Exercice 7 :

De la même façon que représente la distance entre le nombre réel et 3,

exprimer en termes de distance :

a) b) $|x-\frac{1}{3}|$

c) d)

e) f) $|\pi-x|$

Exercice 8 :

Déterminer l’ensemble, sous la forme d’intervalle, des réels vérifiant :

a) $||x-10|\leq\, 1$ b) $|x-2,5|\leq\, 0,2$ c) $|x-\frac{1}{2}|\leq\, \frac{5}{2}$

Exercice 9 :

On considère un intervalle [a ; b] avec a et b deux nombres réels.

On appelle centre de l’intervalle [a ; b] le nombre $c=\frac{a+b}{2}$
et rayon de l’intervalle [a ; b] le nombre $r=\frac{b-a}{2}$ .
Graphiquement, on a :

1. a) Calculer le centre et le rayon de [2 ; 6].

b) Traduire |x – 4| en termes de distance entre deux réels.
c) Recopier et compléter: $x\in[2;6]\Leftrightarrow |x-4|\leq\, ...$

2. De la même manière, recopier et compléter :
a) $x\in[1;25]\Leftrightarrow |x-13|\leq\, ...$ .
b) $x\in[6;20]\Leftrightarrow |x-...|\leq\, ...$
c) $x\in[1,2;3]\Leftrightarrow |x-...|\leq\, ...$

Exercice 10 :

Ecrire une inégalité vérifiée par et utilisant une valeur absolue dans les cas suivants.

a) $x\in [-4;5]$ b) $x\in [0;1,1]$ a) $x\in [ \frac{1}{3};\frac{2}{3}]$

Exercice 11 :

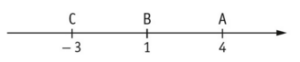
On donne un axe gradué, sur lequel on a placé les points A, B et C.

Compléter les pointillés.

a. AB = …. b. AC = … c. BC = … d. CC = …

Exercice 12 :

On donne un axe gradué, sur lequel on a placé les points A, B et C.

Compléter les pointillés.

a. AB = …. b. AC = … c. BC = …

Exercice 13 :
Ecrire sans les barres de valeurs absolues les nombres :

$a.\,|\,(1-\sqrt{2})\,^2\,|$

$b.\,|\,2\sqrt{2}-\sqrt{3}|$

$c.\,|\,6-2\pi\,|$

$d.\,\frac{\,|\,-2|}{|\,-5+1|}$

Exercice 14 :

Résoudre dans $\mathbb{R}$ les équations suivantes :

$a.\,|x\,|=5\\b.\,|-x\,|=19\\c.\,|x-7\,|=0\\d.\,|x+5,4\,|=0\\e.\,|x-5\,|=8\\f.\,|x-\frac{7}{2}\,|=2$

Exercice 15 :

Résoudre dans $\mathbb{R}$ les inéquations suivantes :

$a.\,|x-2\,|\leq\,\,5\\\,b.\,|x-5\,|\leq\,\,1\\\,c.\,|x+1,5\,|+2,5<\,6\\\,d.\,|x-\sqrt{3}\,|\,<\,\sqrt{3}\\\,e.\,|x-2\,|\,\geq\,\,\sqrt{3}\\\,f.\,|x+\pi\,|\,<\sqrt{5}$

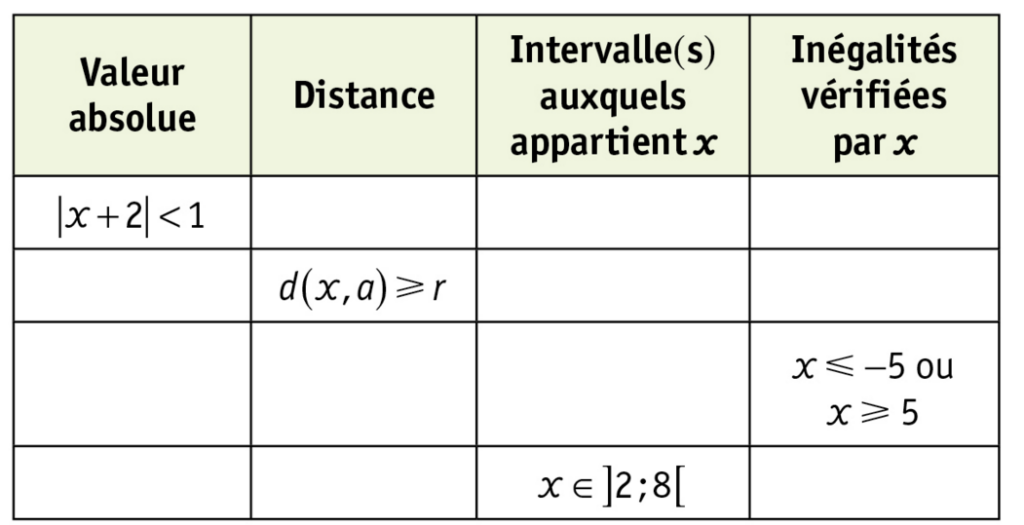
Exercice 16 :

Recopier et compléter le tableau ci-dessous :

Enoncé	Intervalle	Représentation graphique
$-1\leq\,\,x<3$	x $\in$
	x $\in$
$-7\geq\,\,x>\,-8$	x $\in$
$x\in\,\mathbb{R}^+$	x $\in$
$x\neq\,5$	x $\in$

Exercice 17 :

Traduire sous forme d’intervalle :

1) y > – 3 et y < 4 2) y > – 3 ou y < 4

3) $y\leq\,\,\frac{1}{3}$ et $y\leq\,\,\frac{1}{2}$ 4) $y\leq\,\,\frac{1}{3}$ ou $y\leq\,\,\frac{1}{2}$

Exercice 18 :

Compléter avec les symboles $\in$ ou $\notin$ :

1) 7 … ] 0 ; 7 [

2) 5,9 … ] 5,8 ; +∞ [

3) – 0,25 … ] – 0,3 ; – 0,2 [ … ] 1 ; 2 ]

4) – 0,199 … ] – 0,2 ; – 0,19 [

5) $\pi$ …. [ 3,14 ; 3,141 [

Exercice 19 :

Vrai ou faux ?

1) Si x ∈ [ 6,7 ; +∞ [ alors x ∈ [ 6 ; +∞ [.

2) Si x ∈ ] – 3 ; 4 [ alors x ∈ [ – 2 ; 5 [.

3) Si x ∉ [ – 5 ; 2[ alors x ∈ ] $-\infty$ ; – 3 [ ∪ [ 2 ; +∞[.

4) L’intervalle ] 0 ; 4[ est inclus dans [ 0 ; 4 [.

5) $\mathbb{N}\,\subset\,\mathbb{Q}^+$ .

6) Si $x\,\notin\,\mathbb{Q}$ alors $x\,\notin\,D$ .

Exercice 20 :

Simplifier les notations suivantes lorsque c’est possible.
A = [ – 5 ; 7[ ∪ [ – 2 ; 12 [
B = [ 0 ; +∞ [ ∪ ] – 2 ; +∞ [
C = ] –∞ ; 0 [ ∪ [ 0 ; +∞ [
D = ] -∞ ; 4/3 [ ∩ [ – 10 ; 10 ]
E = [ – 4 ; [ ∪ ] $\frac{1}{2}$ ; 10]

Exercice 21 :

Représenter I et J sur une droite graduée, puis déterminer I ∩ J et I ∪ J.

1) I = [ 2 ; 5,5 ] et J = ] 1 ; 3 ].

2) I = [ – 1 ; +∞ [ et J = ] –2 ; 3 ].

3) I = ] – 1 ; 3 ] et J = [ – $\sqrt{2}$ ; $\pi$ [.

4) $I\,=\,\mathbb{R}^-$ et $J\,=\,\mathbb{R}^+$ .

5) I = {1 ; 2 ; 3 ; 4} et J = [ – 5 ; 5 ].

Exercice 22 :

On considère des droites graduées sur lesquelles on a marqué des ensembles de nombres.

Donner l’intervalle correspondant.

Exercice 23 :

Représenter sur une droite graduée et décrire, à l’aide d’un intervalle, chacun des ensembles de nombres réels tels que :

a) $0\leq\,\,x\leq\,\,3$ b)

c) $x\leq\,\,9$ d)

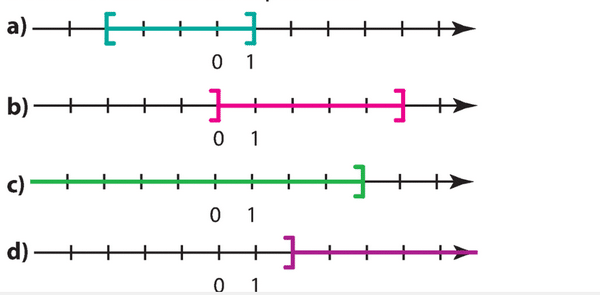
Exercice 24 :

Représenter sur une droite graduée chacun des intervalles suivants.

a) b)

c) $]-\infty;2]$ d) $[0;+\infty[$

Exercice 25 :

Ecrire les inégalités vérifiées par les réels pour chacun des cas suivants.

a) $x\in[0;1,2]$ b) $x\in]-\frac{5}{3};3]$

c) $x\in[4,73;+\infty[$ d) $x\in\,]-\infty;0[$

Exercice 26 :

Recopier et compléter par les signes $\in$ et $\notin$ .

a) b) $-\pi...]-3;-1[$

c) $6...[\frac{7}{3};+\infty[$ d) $-3...\,]-\infty;-3,5[$

Exercice 27 :

Sans calculatrice, dire si $\frac{2}{3}$ appartient aux intervalles suivants.

a) $[0;\frac{4}{5}]$ b) $[\frac{3}{5};1]$ c) $[\frac{1}{3};\frac{2}{5}]$

Exercice 28 :

Soit et .

Dire si chacun des nombres suivants appartient à I, à J, à $I\cap\,J$ , à $I\cup\,J$ .

a) – 10 b) – 6 c) – 0,5 d) 2

e) 8,1 f) 99,9 g) 1 000 h) 0

Exercice 29 :

Compléter le tableau suivant :

Exercice 30 :

Parmi les affirmations suivantes, lesquelles sont vraies ?
Justifier.
a. Quels que soient les réels a et b, $|a\,+\,b|\,=\,|a|\,+|b|$ .
b. Si alors x=0.
c.
d. .