Triangle et quadrilatère : exercices de maths en 6ème corrigés en PDF.
Mis à jour le 19 janvier 2026
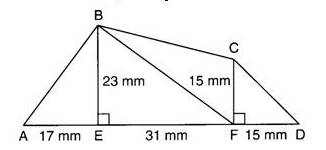
Exercice 1 – Construction de figures géométriques
1. Reproduire cette figure sur votre feuille, en respectant les mesures.
2. Démontrer que les droites (BE) et (CF) sont parallèles.
Exercice 2 – Construction de triangles et cercles
Toutes les longueurs sont exprimées en cm.
1.Tracer un segment [RS] de 6 cm.
2.Construire les points A, B, C, D, E, F, G, H, I, J, K, et L sachant que :
– Tous les points sont situés à 6 cm de S
– A et B sont tels que RA = RB = 1
– C et D sont tels que RC = RD = 3
– E et F sont tels que RE = RF = 5
– G et H sont tels que RG = RH = 7
– I et J sont tels que RI = RJ = 9
– K et L sont tels que RK = RL = 11
3. Tracer tous les triangles ayant pour sommets R, S et l’un des points construits
précédemment.
4. Coder les longueurs égales sur cette figure.
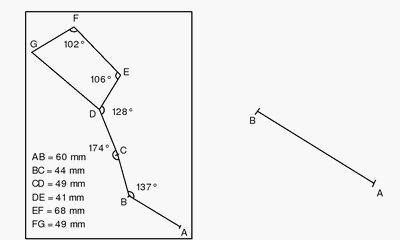
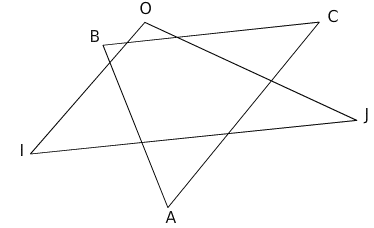
Exercice 3 – Quadrilatère et construction de la grande ourse
Reproduire la figure ci-dessous à l’aide de la règle et du rapporteur .
Cette figure représente la grande ourse .
La Grande Ourse est la troisième plus grande constellation du ciel.
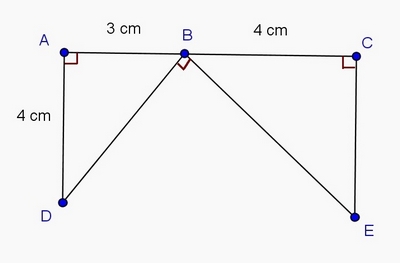
Exercice 4 – Programme de construction
Voici une figure où les points A, B et C sont alignés .
a. Rédiger un programme de construction de cette figure .
b. Reproduire cette figure sur papier blanc avec les instruments de géométrie .
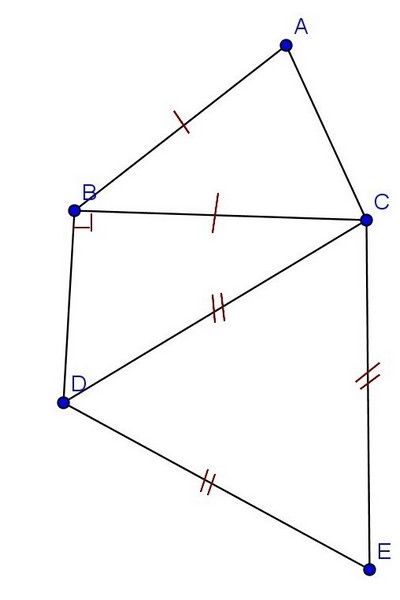
Exercice 5 – Quadrilatère inscrit dans un triangle
a. Tracer un triangle ABC tel que AB = 3 cm, AC = 5 cm et .
b. Placer le point M sur le segment [AB] tel que AM = 1 cm .
c. Par M, tracer la parallèle à la droite (BC); elle coupe la droite (AC) en N.
d. Par M, tracer la perpendiculaire à la droite (BC); elle coupe (BC) en Q.
Par N, tracer la parallèle à la droite (MQ) ; elle coupe (BC) en P.
e. Que peut-on dire des droites (MQ) et (MN) ?
Expliquer pourquoi .
f. Que peut-on dire des droites (NP) et (PQ) ?
Expliquer pourquoi .
g. Quelle est la nature du quadrilatère MNPQ ?
Expliquer pourquoi .
Exercice 6 – Triangle rectangle et angles
a. Sur papier blanc, tracer un triangle ABC rectangle en A tel que AB = 5 cm et AC = 8 cm .
b. Placer sur l’hypoténuse [BC] le point E tel que .
c. Sur la demi-droite [EA), placer le point F tel que :
d. Calculer la mesure de chacun des angles suivants, en expliquant votre réponse :
Exercice 7 – Construction de triangles
1. ABC est un triangle isocèle en A tel que AB = 5 cm et BC = 4 cm .
2. DEF est un triangle isocèle en E tel que EF = 6 cm et .
3. GHI est un triangle équilatéral de côté de longueur 4 cm .
4. JKL est un triangle rectangle en L tel que JL = 5 cm et KL = 6 cm .
5. PQR est un triangle rectangle isocèle en Q tel que QR = 4 cm .
Exercice 8 – Donner la nature d’un triangle
Dans chaque cas, faire la figure décrite et
indiquer la nature du triangle.
a. ABC est un triangle tel que .
b. MNP est un triangle tel que MN=NP et .
c. EFG est un triangle isocèle en chacun de ses sommets .
Exercice 9 – Construction de triangle et parallèles
a. Tracer un triangle ABC.
b. Par le point A, tracer la droite (d) parallèle à la droite (BC) .
Par le point B, tracer la droite (d’) parallèle à la droite (AC); elle coupe (d) en E .
Par le point C, tracer la droite (d ») parallèle à la droite (AB); elle coupe (d) en F et (d’) en G.
c. Tracer les droites (EC), (BF) et (AG) .
Que remarques – tu ?
Exercice 10 – Construction de figure à l’aide de données graphiques et numériques
Voici une figure dessinée à main levée et des informations sur des longueurs .
Faire cette figure sur papier blanc avec les instruments de géométrie .
CE= 6 cm et AC = 3 cm .
Exercice 11 :
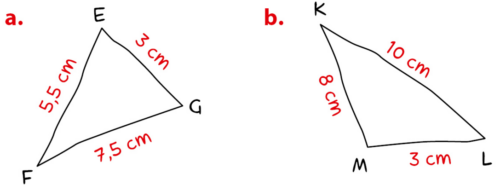
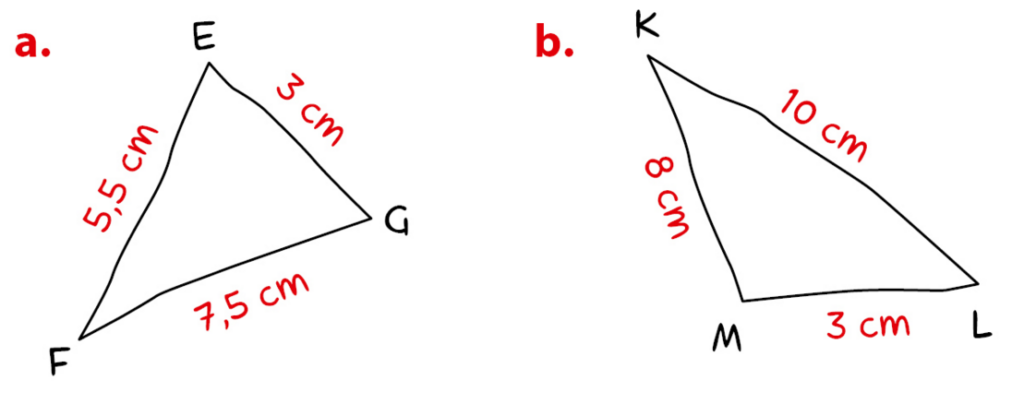
Construire en vraie grandeur chacun des triangles tracés ci-dessous à main levée.
Exercice 12 :
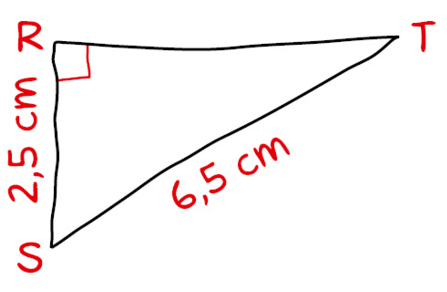
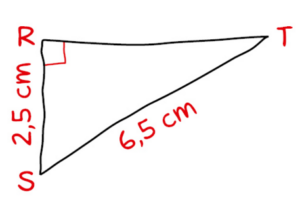
Construire en vraie grandeur le triangle RST tracé ci-contre à main levée.
Exercice 13 :
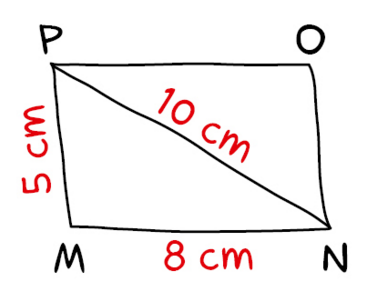
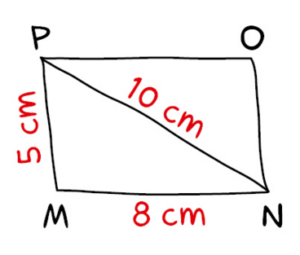
Construire en vraie grandeur ce parallélogramme tracé à main levée.
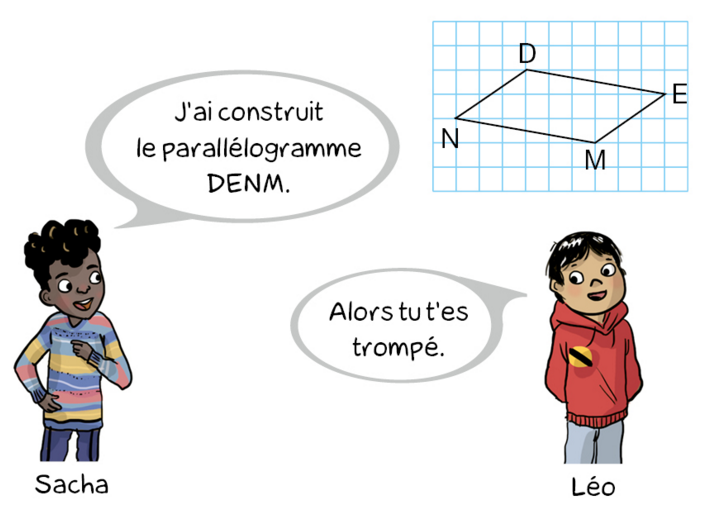
Exercice 14 :
a. Qui de Sacha ou Léo a raison ? Expliquer.
b. Sur papier quadrillé, placer les points M, E et D comme Sacha, puis construire le point N.
Exercice 15 :
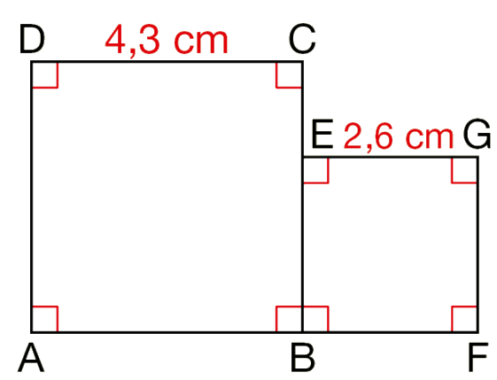
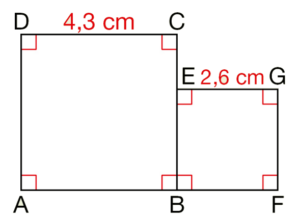
ABCD et BEGF sont deux carrés.
Calculer mentalement les longueurs AF et CE.
Exercice 16 :
On considère le triangle ABC ci-dessous :
- Quels sont ses sommets ?
- Quels sont ses côtés?
- Quel est le côté opposé au sommet B?
- Quel est le sommet opposé au côté [AB] ?
Exercice 17 :
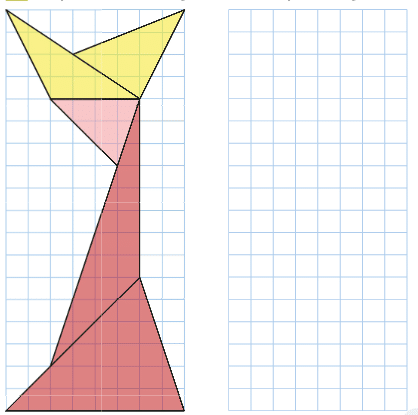
Reproduire cette figure dans le quadrillage vierge.
Exercice 18 :
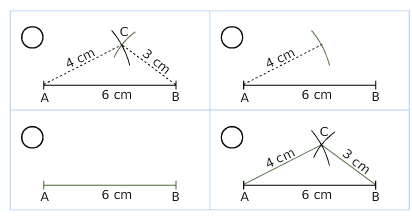
Numéroter chaque image dans l’ordre de la construction du triangle puis décrire
chaque étape de cette construction.
Exercice 19 :
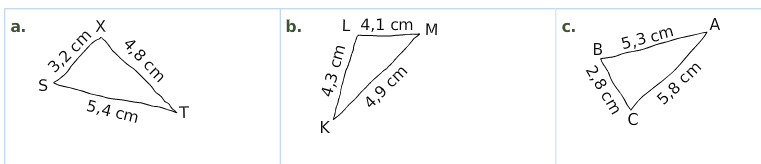
Les dessins suivants sont tracés à main levée.
Construire chaque triangle en vraie grandeur.
Exercice 20 :
Construire les triangles suivants :
- Trace un triangle tel que AB = 7 cm; BC = 5 cm et CA = 6 cm.
- Trace un triangle DEF tel que DE = 6,2 cm; EF = 4,8 cm et DF = 9,1 cm.
- Trace un triangle GHI tel que GH = 7,5 cm; HI =5,1 cm et GI = 5,6 cm.
- Trace un triangle JKl tel que JK = 5,8 cm; LK = 5 cm et JL = 4 cm.
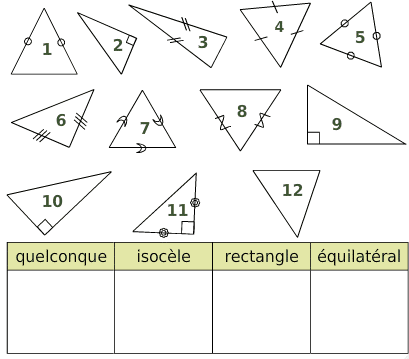
Exercice 21 :
Classer les triangles suivants dans le tableau :
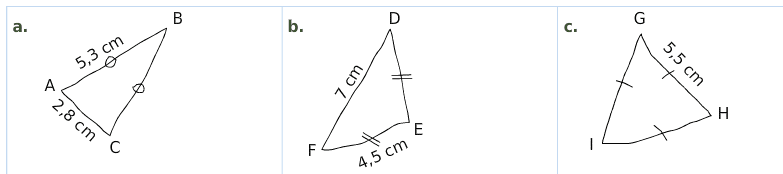
Exercice 22 :
Reproduire chaque triangle ci-dessous en respectant les dimensions et les codages indiqués.
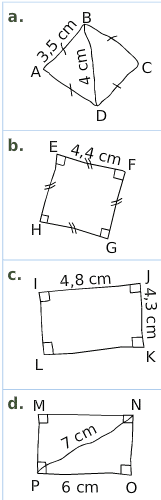
Exercice 23 :
Reproduire chaque quadrilatère ci-dessous, en respectant les dimensions et codages indiqués.
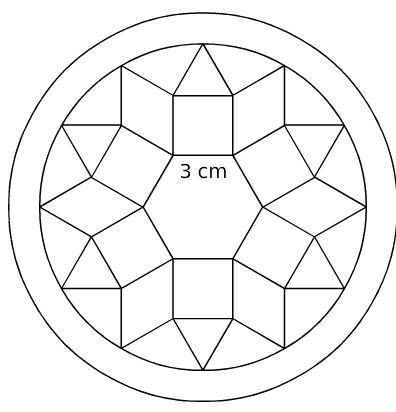
Exercice 24 : étoile de Pompéi.
Tracer d’abord l’hexagone régulier du centre puis poursuivre la construction sachant
que les polygones sont des carrés, des losanges et des triangles équilatéraux.
Exercice 25 :
Construire en vraie grandeur chacun des triangles tracés ci-dessous à main levée.
Exercice 26 :
Construire en vraie grandeur le triangle RST tracé ci-dessous à main levée.
Exercice 27 :
Jenny et Morgan ont construit un triangle ABC tel que AB = 6 cm, AC = 8 cm, BC = 10 cm.
Jenny : « En tournant dans le sens des aiguilles d’une montre, je lis le mot BAC. »
Morgan :« Moi,je lis un mot anglais. »
Est-ce possible ?
Si oui, construire ces triangles.
Exercice 28 :
Construire un parallélogramme DEFG tel que :
ED=5 cm, EF=4cm, DF=7 cm.
Exercice 29 :
Construire en vraie grandeur ce parallélogramme tracé à main levée.
Exercice 30 :
Dans chaque cas, dire si le triangle est isocèle, équilatéral ou ni l’un ni l’autre.
a. AB = 2,5 cm, AC =6 cm, BC = 4,5 cm.
b. MN = 3 cm, MP = 2 cm, NP = 3 cm.
c. RS = 10 cm, RT = 9,5 cm, ST = 9 cm.
Exercice 31 :
ABCD et BEGF sont deux carrés.
Calculer mentalement les longueurs AF et CE.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «triangle et quadrilatère : exercices de maths en 6ème corrigés en PDF.» au format PDF.
Ressources de sixième
Cours de sixième
D'autres cours et exercices à consulter
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.