Représentations paramétriques et équations cartésiennes : exercices de maths en terminale en PDF.

Représentations paramétriques et équations cartésiennes avec des exercices de maths en terminale corrigés en PDF. Nous utiliserons les différentes propriétés et les coordonnées du vecteur normal à un plan. Ces exercices disposent de leur correction afin que les élèves puissent repérer leurs erreurs.

Exercice 1 :

Dans un repère orthonormé de l’espace, et sont les droites de représentations paramétriques
respectives :

$\{\begin{matrix}\,x=1+2t\\\,y=2+t\,\\\,z=-1+2t\,\end{matrix}.$ $(t\in\mathbb{R})$ $\{\begin{matrix}\,x=4t'\\\,y=-2-t'\,\\\,z=2+t'\,\end{matrix}.$ $(t\in\mathbb{R})$ $(t'\in\mathbb{R})$

a) Montrer que les droites et ne sont pas parallèles.
b) Étudier l’intersection de et en résolvant un système d’équations.

Exercice 2 :

et $(d\,')$ sont deux droites de représentations paramétriques respectives :

$\{\begin{matrix}\,x=1+2t\\\,y=-3+t\,\\\,z=5t\,\end{matrix}.$ $(t\in\mathbb{R})$ $\{\begin{matrix}\,x=2-3t'\\\,y=-2t'\,\\\,z=1-t'\,\end{matrix}.$ $(t'\in\mathbb{R})$

Indiquer oralement les coordonnées d’un point et d’un vecteur directeur de chacune des droites et $(d\,')$ .

Exercice 3 :

est la droite de représentation paramétrique :

$\{\begin{matrix}\,x=-t+1\\\,y=5+3t\,\\\,z=-2-2t\,\end{matrix}.$ $(t\in\mathbb{R})$

Déterminer mentalement les coordonnées de quatre points de la droite .

Exercice 4 :

On donne les points :

Parmi ces systèmes, une représentation paramétrique de la droite (AB) est :

$(1)\{\begin{matrix}\,x=1+3t\\\,y=2+3t\,\\\,z=1-3t\,\end{matrix}.$ $(t\in\mathbb{R})$

$(2)\{\begin{matrix}\,x=3+t'\\\,y=3+2t'\,\\\,z=-3+t'\,\end{matrix}.$ $(t'\in\mathbb{R})$

$(3)\{\begin{matrix}\,x=4+3m\\\,y=5+3m\,\\\,z=-2-3m\,\end{matrix}.$ $(m\in\mathbb{R})$

$(4)\{\begin{matrix}\,x=4-k\\\,y=5-k\,\\\,z=-2+k\,\end{matrix}.$ $(k\in\mathbb{R})$

Exercice 5 :

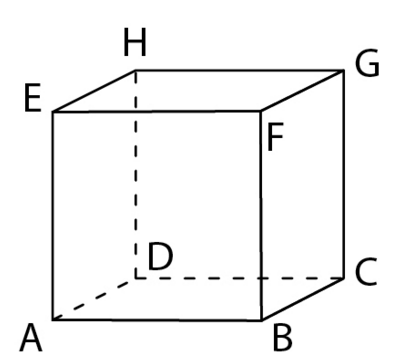
ABCDEFGH est le cube représenté ci-dessous.
a) Déterminer les coordonnées de chacun des sommets dans le repère $(A\,;\,\vec{AB},\,\vec{AD},\,\vec{AE})$ .

b) Déterminer une représentation paramétrique de chacune des droites (AG) et (BH).

Exercice 6 :

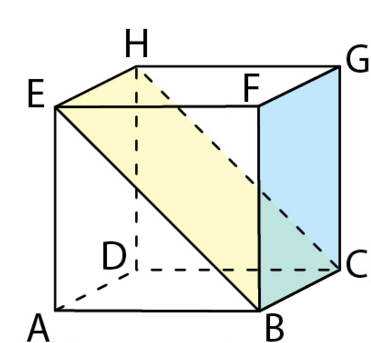
ABCDEFGH est le cube représenté ci-contre.
Pour chacun des plans ci-dessous, indiquer oralement deux vecteurs normaux.
a) (ABC)

b) (BCF)

c) (ADF)

Exercice 7 :

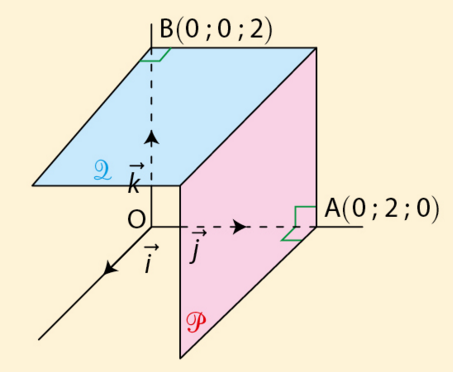
Déterminer une équation cartésienne du plan :
a) coloré en rouge passant par le point A et orthogonal à l’axe des ordonnées ;
b) $(\wp\,)$ coloré en bleu passant par le point B et orthogonal à l’axe des côtes.

Exercice 8 :

On se place dans le repère orthonormé $(A\,;\,\vec{AB},\,\vec{AD},\,\vec{AE})$ .
a) Déterminer les coordonnées d’un vecteur normal au plan (BCF), puis au plan (BCE).

b) Déterminer une équation cartésienne du plan (BCF), puis du plan (BCE).

Exercice 9 :

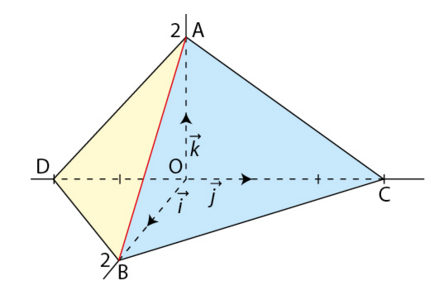
On a placé quatre points A, B, C, D dans le repère orthonormé ci-dessous.

a) Lire les coordonnées des points A, B, C, D.
b) Démontrer que le vecteur $\vec{n}(3\,;\,2\,;\,3)$ est normal au plan (ABC) ; puis que le vecteur $\vec{\,m}(1\,;\,-\,1\,;\,1)$ est normal au plan (ABD).
c) Déterminer une équation cartésienne du plan (ABC), puis du plan (ABD).
d) Alix affirme « Le point $E(-\,10\,;-15;-3)$ appartient à l’un des deux plans ».

A-t-elle raison ?

Exercice 10 :

et $(d\,')$ sont les droites de représentations paramétriques respectives :

$\{\begin{matrix}\,x=t\\\,y=1+t\,\\\,z=3-t\,\end{matrix}.$ $(t\in\mathbb{R})$ et $\{\begin{matrix}\,x=2-t'\\\,y=t'\,\\\,z=-2+3t'\,\end{matrix}.$ $(t'\in\mathbb{R})$

Déterminer mentalement lequel de ces systèmes on est amené à résoudre pour déterminer l’inter
section de et $(d\,')$ .

$(1)\{\begin{matrix}\,t+t'=2\\\,t-t'=1\,\\\,t+3t'=-5\,\end{matrix}.$ et $(2)\{\begin{matrix}\,t+t'=2\\\,t-t'=-1\,\\\,t+3t'=5\,\end{matrix}.$

Exercice 11 :

Voici les représentations paramétriques respectives de deux droites et $(d\,')$ sécantes.
Déterminer leur point d’intersection.

$\{\begin{matrix}\,x=1-t\\\,y=2t\,\\\,z=4\,\end{matrix}.$ $(t\in\mathbb{R})$ et $\{\begin{matrix}\,x=2+t'\\\,y=-2-2t'\,\\\,z=t'\,\end{matrix}.$ $(t'\in\mathbb{R})$

Exercice 12 :

et $(d\,')$ sont les droites de représentations paramétriques respectives :

$\{\begin{matrix}\,x=5-t\\\,y=2+t\,\\\,z=1-3t\,\end{matrix}.$ $(t\in\mathbb{R})$ et $\{\begin{matrix}\,x=t'\\\,y=2-2t'\,\\\,z=1+t'\,\end{matrix}.$ $(t'\in\mathbb{R})$

a) Démontrer que et $(d\,')$ ne sont pas parallèles.
b) Démontrer que et $(d\,')$ ne sont pas coplanaires en résolvant un système d’équations.

Exercice 13 :

a et b désignent des nombres réels.

On donne les points $A(1\,;\,1\,;\,a),\,B(3\,;\,a\,;\,b),\,C(-3;b;\,2a\,+\,1)$ .

On se propose de déterminer a et b afin que les points A, B, C soient alignés.

a) Déterminer les coordonnées des vecteurs $\vec{AB}$ et $\vec{AC}$ .
b) Montrer que les points A, B, C sont alignés si, et seulement si,

$\{\begin{matrix}\,b-1=-2(a+1)\\\,a+1=-2(b-a)\,\end{matrix}.$

c) Résoudre ce système et conclure en donnant les coordonnées de A, B, C.

Exercice 14 :

est un plan d’équation cartésienne :
$ax\,+\,by\,+\,z\,+\,d\,=\,0$ (avec a et b nombres réels).
Existe-t-il des nombres a et b tels que les points appartiennent
au plan .

Exercice 15 :

est le plan d’équation cartésienne :

.
A est le point de coordonnées $(2\,;\,0;-1).$
a) Déterminer une représentation paramétrique de la droite $\Delta$ passant par A et perpendiculaire au plan .
b) En déduire les coordonnées du point H, projeté orthogonal du point A sur le plan .

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «représentations paramétriques et équations cartésiennes : exercices de maths en terminale en PDF.» au format PDF.

D'autres cours et exercices à consulter

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.