Brevet de maths 2023 : sujet pour réviser le brevet en ligne.

Sommaire

Un sujet du brevet blanc de maths 2023 afin de réviser en ligne sur Mathovore et de se préparer pour les épreuves du brevet des collèges en juin 2023.

Brevet blanc de maths 2023

L’orthographe, le soin, la qualité et la précision de la rédaction seront pris en compte à hauteur de 4 points sur 40 dans l’évaluation de la copie. L’utilisation de la calculatrice est autorisée.
Aucun prêt de matériel n’est autorisé. Conserver le sujet pour correction.

Exercice 1 : ( 4 points )

Cet exercice est un questionnaire à choix multiples (QCM). Aucune justification n’est demandée.
Pour chacune des questions, trois réponses sont proposées ; une seule est exacte.
Chaque bonne réponse donne un point, une réponse fausse ou une absence de réponse n’enlève aucun point.
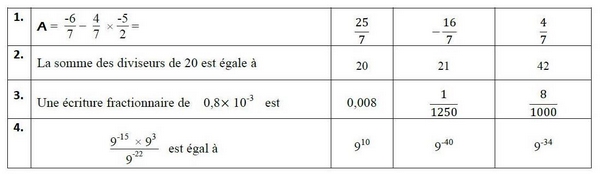
Pour chacune des quatre questions, indiquer sur la copie le numéro de la question et recopier la réponse exacte.

Exercice 2 : ( 4,5 points )

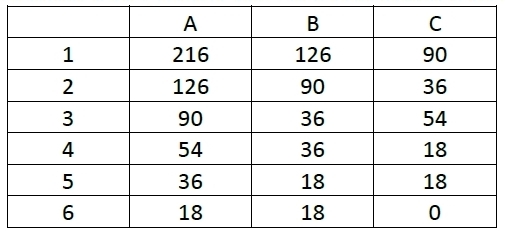
Voici une feuille de calcul obtenue à l’aide d’un tableur ; dans cet exercice on cherche à comprendre comment cette feuille a été remplie.

1. En observant les valeurs du tableau, proposer une formule à entrer dans la cellule C1, puis à recopier vers le bas.
2. Dans cette question, on laissera sur la copie toutes les traces de recherche : elles seront valorisées. Le tableur fournit deux fonctions MAX et MIN. À partir de deux nombres, MAX renvoie la valeur la plus grande et MIN la plus petite. (exemple : MAX(23 ;12) = 23) Quelle formule a été entrée dans la cellule A2, puis recopiée vers le bas ?
3. Que représente le nombre figurant dans la cellule C5, par rapport aux nombres 216 et 126 ?
4. La fraction 216/126 est-elle irréductible ? Si ce n’est pas le cas, la rendre irréductible en détaillant les calculs.

Exercice 3 : ( 4,5 points )

Le parcours de cyclisme est une boucle de 10 km. Le point de départ est donc aussi le point d’arrivée.
À mi-parcours, les athlètes ont droit à un ravitaillement.
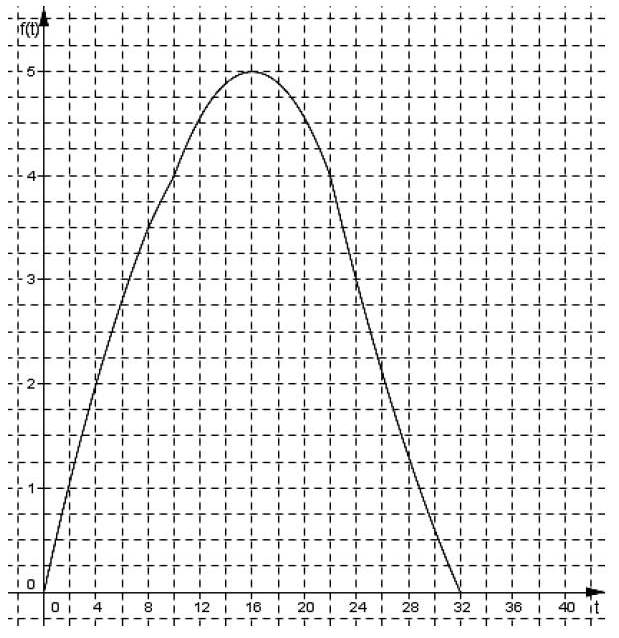
Le graphique ci-dessous représente la distance f(t) exprimée en kilomètres séparant Hélène du point d’arrivée en fonction du temps t exprimé en minutes.
On appelle f la fonction ainsi représentée.
Toutes les réponses seront données à l’aide du graphique.

1) Combien de kilomètres reste-t-il à parcourir au bout de 24 minutes ?
2) Déterminer l’image du nombre 4 par la fonction f.
3) Déterminer f(8).
4) Déterminer le ou les antécédent(s) du nombre 0 par la fonction f.
5) Pour quelle(s) valeur(s) de t a-t-on f(t) = 4 ?

Exercice 4 : ( 3 points )

Il existe différentes unités de mesure de température : en France on utilise le degré Celsius (°C), aux États-Unis on utilise le degré Fahrenheit (°F).
Pour passer des degrés Celsius aux degrés Fahrenheit, on multiplie le nombre de départ par 1,8 et on ajoute 32 au résultat.
1°) Qu’indiquerait un thermomètre gradué en degrés Fahrenheit si on le plonge dans une casserole d’eau qui gèle ? On rappelle que l’eau gèle à 0°C.
2°) Qu’indiquerait un thermomètre en degrés Fahrenheit si on le plonge dans une casserole d’eau à 23°C ?
3°) Si on appelle x la température en degrés Celsius et f(x) la température en degrés fahrenheit, exprimer f(x) en fonction de x.

Exercice 5 : ( 3 points )

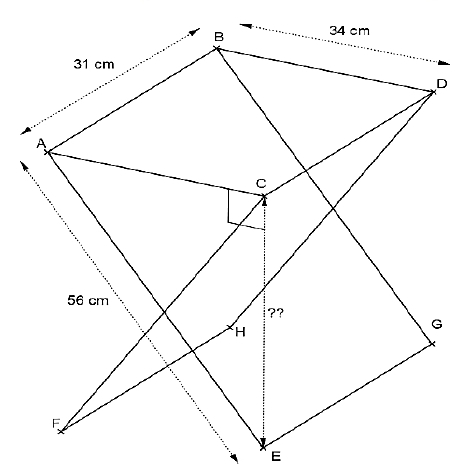
Pour une bonne partie de pêche au bord d’un canal, il faut un siège pliant adapté ‼
Nicolas est de taille moyenne et pour être bien assis, il est nécessaire que la hauteur de l’assise du siège soit comprise entre 44 cm et 46 cm.
L’angle $\widehat{ACE}$ est droit et ABDC est un rectangle.
La hauteur de ce siège lui est-elle adaptée ?

Exercice 6 : ( 5 points )

Un fût de déchets radioactifs (représenté ci-contre) a la forme d’un cylindre de rayon 0,6 mètre et de hauteur 1,5 mètre.

a) Calculer le volume d’un seul fût. On donnera la valeur exacte et la valeur arrondie au dm3 près.
b) On veut stocker ces fûts au contenu dangereux dans des bassins de stockage souterrains de forme parallélépipédique (voir photo).
Si l’on dispose d’un bassin de longueur 360 mètres, de largeur 150 m et de hauteur 9 mètres,
montrer que l’on peut alors y stocker 225 000 fûts.

c) Quel est le pourcentage d’espace perdu dans le bassin de stockage ?
Le résultat sera arrondi au dixième.

Exercice 7 : ( 4 points )

Attention les figures tracées ne respectent ni les mesures de longueur, ni les mesures d’angles.
Répondre par « vrai » ou « faux » ou « on ne peut pas savoir » à chacune des affirmations suivantes et expliquer votre choix.
1. Tout triangle inscrit dans un cercle est rectangle.
2. Si un point M appartient à la médiatrice d’un segment [AB], alors le triangle AMB est isocèle.
3. Dans le triangle ABC suivant : $\widehat{ACB},=,30^{\circ}$ .

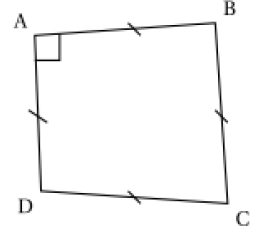
4. Le quadrilatère ABCD ci-dessous est un carré.

Exercice 8 : ( 4 points )

Voici une carte découverte par Marco qui lui permettra de déterrer le fabuleux trésor de Batmath le pirate.
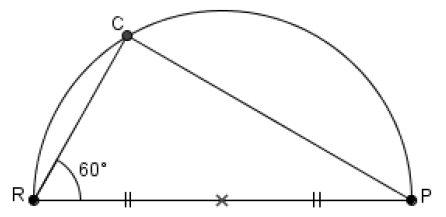
Les indications sont : R est le rocher en forme de crâne ; C le cocotier sous lequel est enterré le trésor ; P est le phare ; C est situé sur le demi-cercle de diamètre [PR].

On donne PR = 3000 brasses (ancienne unité de mesure de longueur correspondant à l’envergure des bras)

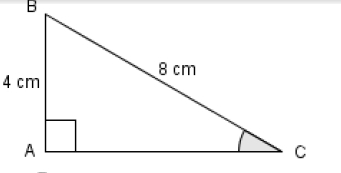
a) Démontrer que le triangle PRC est un triangle rectangle.
b) Calculer la distance RC en brasses.

Exercice 9 : exercice à prise d’initiative.

Michel possède 108 billes blanches et 135 billes noires qu’il veut vendre à la brocante près de chez lui. Pour cela, il veut préparer le plus grand nombre possible de sachets identiques (même nombre de billes blanches et même nombre de billes noires dans chaque sachet) en utilisant toutes ses billes.
Combien pèse un sachet de billes ?
Combien Michel pourra – t – il gagner au maximum en vendant ses sachets ?

Laisser une trace écrite de vos recherches, même incomplètes.
Elles seront prises en compte dans la notation.

Consulter le corrigé en ligne

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet de maths 2023 : sujet pour réviser le brevet en ligne.» au format PDF.

D'autres cours et exercices à consulter

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.