I.Série statistique
1.Vocabulaire
L’effectif d’une valeur est le nombre de fois où cette valeur apparaît dans la série statistique.L’effectif total est égal au nombre de donnée de la série.
Exemple 1 :
La classe d’Alexandre est composée de 22 élèves. Il interroge ses camarades pour savoir à combien d’écrans ( télévisions, tablette, téléphone, ordinateur,..) ils peuvent facilement accéder à leur domicile.Voici leurs réponses :
3-5-1-4-2-3-3-2-4-4-5-1-3-3-2-5-4-4-3-2-2-3
La population étudiée est composée des élèves de la classe.
Les individus sont les élèves de la classe.
Le caractère étudié est le nombre d’écrans accessibles.
Le caractère prend différentes valeurs dans cette série : 1,2,3,4 ou 5.
Dans cette série, le caractère est dit quantitatif car on peut le mesurer à l’aide de nombres.
On peut regrouper l’ensemble des données dans un tableau d’effectifs.
Pour déterminer l’effectif de la valeur 2, on compte le nombre de fois où 2 apparaît dans la série : il apparaît 5 fois.
Remarque :
On peut vérifier que lorsque l’on rajoute tous les effectifs, on retrouve l’effectif total :2+5+7+5+3=22.
Exemple 2 :
Dans un club de judo, les 32 judokas se répartissent de la façon suivante :
La population étudiée est composée de 32 judokas.
Le caractère étudié est la catégorie.
Le caractère est qualitatif (poussins, benjamins,…) car on ne peut pas le mesurer avec des nombres.
2.Fréquence de séries statistiques
La fréquence d’une valeur est le quotient 
.
Elle peut être exprimée sous forme décimale (exacte ou approchée) ou fractionnaire.
Dans le cas de pourcentage, on parle de fréquence en pourcentage.
Exemple 1 :
Dans le cas d’Alexandre, 7 élèves sur 22 ont répondu 3.
La fréquence de la valeur 3 est donc %.
Exemple 2 :
Dans le cas du tatami.
Parmi les 32 judokas du club, 32 sont poussins.
La fréquence des poussins est donc soit 21,875 %.
Remarque :
La somme des fréquence donc 100, c’est-à-dire 100 % pour les séries statistiques.
II.Les indicateurs (caractère quantitatifs)
1.La moyenne
La moyenne d’une série statistique est la moyenne des valeurs de la série rapportée au nombre d’individus, c’est-à-dire la somme des valeurs rapportées à l’effectif total.
Pour calculer la moyenne M d’une série :
on additionne toutes les valeurs du caractère de la série;
on divise la somme obtenue par l’effectif total.
Si représentent les valeurs du caractère de la série , on a alors :
avec N qui est la valeur de l’effectif total.
Exemple 1 :
Dans la classe d’Alexandre, le nombre moyen d’écrans par élèves est de 3, puisque :
.
2.La médiane
On appelle médiane m d’une série statistiques dont les valeurs sont ordonnées dans l’ordre croissant, tout nombre qui partage cette série en deux sous-séries de même effectif.
Exemple :
Dans la classe d’Alexandre, on commence par ranger les valeurs du caractère par ordre croissant.
1-1-2-2-2-2-2-3-3-3-3-3-3-3-4-4-4-4-4-5-5-5
On les sépare en deux groupes de 11 données.
1-1-2-2-2-2-2-3-3-3-3–3-3-3-4-4-4-4-4-5-5-5
La valeur 3 sépare cette série en deux sous-séries de même effectif donc 3 est la médiane de cette série.
III.Les représentations graphiques
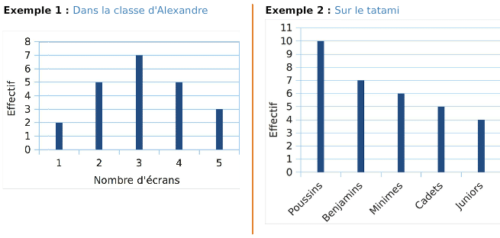
1.Le diagramme en bâtons
Un diagramme en bâtons est un graphique qui à chaque valeur, associe un bâton (segment)
de hauteur proportionnelle à l’effectif correspondant.
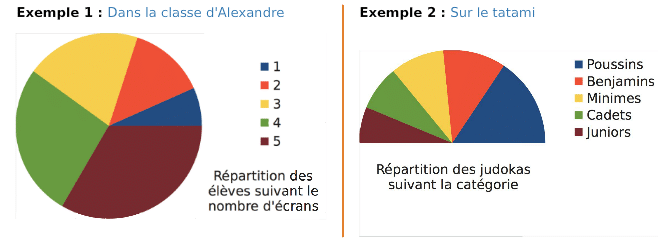
2.Le diagramme circulaire
Un diagramme circulaire est un graphique sous forme de disque qui, à chaque valeur, associe un secteur dont l’angle au centre est proportionnel à l’effectif correspondant.
Remarque :
On parle de diagramme semi-circulaire lorsqu’il est formé d’un demi-disque.
Remarques :
Dans un diagramme circulaire, la somme des angles des secteurs est de 360°.
Dans un diagramme semi-circulaire, la somme des angles des secteurs est égale à 180°.
