BREVET de MATHS 2021
SUJET BLANC N° 3
_______________
Durée de l’épreuve : 2 h 00
_______________
L’utilisation de la calculatrice est autorisée
(circulaire n°99-186 du 16 novembre 1999)
L’usage du dictionnaire n’est pas autorisé
Exercice 1 :
Cet exercice est un QCM (Questionnaire à Choix Multiples).
Pour chaque question il peut y avoir une ou plusieurs réponses, voire au une.
Chaque bonne réponse rapporte 0,5 point, chaque mauvaise réponse annule une bonne réponse.
Pour chacune des questions suivantes, écrivez sans justification le numéro de la question et la (ou les) lettre(s) de la (ou les) bonne(s) réponse(s).
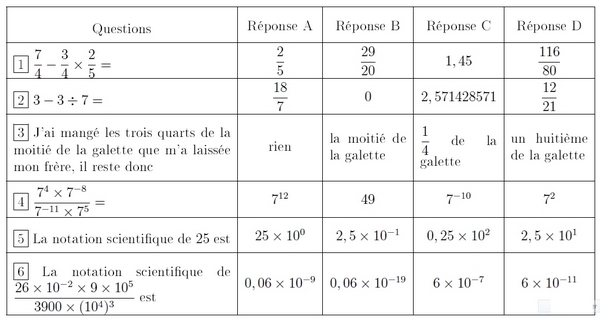
1. Calculez le PGCD de 1755 et 1053.
2. Écrivez la fraction sous la forme irréductible.
3. Un collectionneur de coquillages (un conchyliologue) possède 1755 cônes et 1053 porcelaines.
Il souhaite vendre toute sa collection en réalisant des lots identiques,c’est-à-dire comportant le même nombre de coquillages et la même répartition de cônes et de porcelaines.
(a) Quel est le nombre maximum de lots qu’il pourra réaliser ?
(b) Combien y aura-t-il, dans ce cas, de cônes et de porcelaines par lot ?
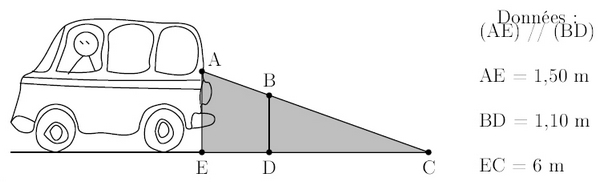
Exercice 3 : Sécurité routière
En se retournant lors d’une marche arrière, le conducteur d’une camionnette voit le sol à 6 mètres
derrière son camion.Sur le schéma, la zone grisée correspond à ce que le conducteur ne voit pas lorsqu’il regarde en arrière.
1. Calculez DC.
2. En déduire que ED = 1,60 m.
3. Une fillette mesure 1,10 m. Elle passe à 1,40 m derrière la camionnette.
Le conducteur peut-il la voir ? Expliquer.
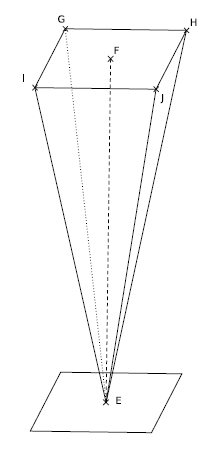
Exercice 4 :
Monsieur Archi et monsieur Mède fêtent l’anniversaire de leur voisine madame Eurêka.
Ils ont tous les trois une flûte de champagne à la main.
Cette flûte est une pyramide à base carré dont le sommet repose sur un socle carré.
On donne :
EF = 12 cm et IG = 4 cm.
1. Montrez que la contenance maximale de chaque flûte est de 64 .
2. Monsieur Archi a rempli chaque flûte aux trois quarts de sa contenance.
Quel volume de champagne y-a-t-il dans chaque flûte ?
3. Le champagne n’étant plus très frais, monsieur Mède va chercher des glaçons de forme cubique
d’arêtes 1, 5 cm.
(a) Quel est le volume de chaque glaçon ?
(b) Un glaçon flotte dans du champagne de telle façon qu’un cinquième de son volume reste au dessus de la surface du champagne (un peu comme un iceberg dans l’océan).
Combien de glaçons au minimum doit mettre monsieur Mède dans la flûte de madame Eurêka pour que le champagne déborde de la flûte ?
Exercice 5 :
Dans le cadre d’un projet pédagogique, des professeurs préparent une sortie au Mont Saint Michel
avec 48 élèves de 3e.
Deux activités sont au programme :
• la visite du Mont et de son abbaye ;
• la traversée à pied de la baie du Mont Saint Michel.
Le coût total de cette sortie (bus, hébergement et nourriture, activités, … ) s’élève à 120 € par élève.
1. Pour réduire le coût de la sortie, les professeurs décident d’organiser une tombola.
Chaque élève dispose d’une carte contenant 20 cases qu’il doit vendre à 2 € la case.
En décembre, les professeurs font le point avec les 48 élèves sur le nombre de cases vendues par chacun d’entre eux.
Voici les résultats obtenus :
(a) Quel est le nombre total de cases déjà vendues en décembre ?
(b) Quelle somme d’argent cela représente-t-il ?
(c) Quel est le pourcentage d’élèves ayant vendu 15 cases ou moins ? (arrondir à l’unité).
(d) Quel est le nombre moyen de cases vendues par élève ? (arrondir à l’unité).
2. Les 92 lots à gagner sont les suivants :
• un vélo ;
• un lecteur DVD;
• 20 DVD;
• 20 clés USB de 4 GO;
• 50 sachets de chocolats.
Ces lots sont fournis gratuitement par trois magasins qui ont accepté de sponsoriser le projet.
Le triage au sort a lieu au mois de mars et les 960 cases ont toutes été vendues.
Une personne a acheté une case.
(a) Quelle est la probabilité que cette personne gagne un lot ? (arrondir au centième)
(b) Quelle est la probabilité que cette personne gagne une clé USB? (arrondir au centième)
Exercice 6 :
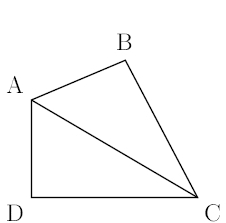
Jean-Michel est propriétaire d’un champ, représenté par le triangle ABC ci-dessous. Il achète à
son voisin le champ adjacent, représenté par le triangle ADC. On obtient ainsi un nouveau champ
formé par le quadrilatère ABCD.
Jean Michel sait que le périmètre de son champ ABC est de 154 mètres et que BC = 56 m.
Son voisin l’informe que le périmètre du champ ADC est de 144 mètres et que AC = 65 m.
De plus, il sait que AD = 16 m.
1. (a) Justifiez que les longueurs AB et DC sont respectivement égales à 33 m et 63 m.
(b) Calculez le périmètre du champ ABCD.
2. Démontrez que le triangle ADC est rectangle en D.
On admet que le triangle ABC est rectangle en B.
3. Calculez l’aire du champ ABCD.
4. Jean-Michel veut clôturer son champ avec du grillage. Il se rend chez son commerçant habituel
et tombe sur l’annonce suivante :
Grillage : 0,85 € par mètre
Combien va-t-il payer pour clôturer son champ ?
Exercice 7 :
Dans cet exercice, toute trace de recherche, même incomplète, sera prise en compte dans l’évaluation.
On peut lire au sujet d’un médicament :
- Chez les enfants (12 mois à 17 ans), la posologie doit être établie en fonction de la surface corporelle du patient [voir formule de Mosteller].
- Une dose de charge unique de 70 mg par mètre carré (sans dépasser 70 mg par jour) devra être administrée .
Pour calculer la surface corporelle en m² on utilise la formule suivante (dite formule de Mosteller) :
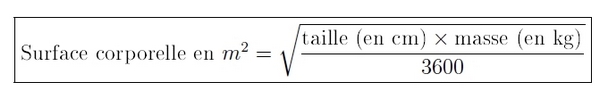
Question : Les posologies ont-elles été respectées pour ces deux enfants ?
Vous arrondirez vos résultats au centième près.






 Mathovore c'est 13 931 212 cours et exercices de maths téléchargés en PDF.
Mathovore c'est 13 931 212 cours et exercices de maths téléchargés en PDF.