Cosinus et trigonométrie : cours de maths en 4ème

Sommaire

Trigonométrie dans le triangle rectangle dans un cours de maths en 4ème sur le cosinus (cos) d’un angle aigu et sa formule ainsi que la résolution de problèmes dans le triangle rectangle. Cette leçon est aussi à télécharger gratuitement au format PDF.

0. Introduction :un peu d’histoire .

Point de vue historique :

Le mot trigonométrie vient du grec « trigone » (triangle) et « metron » (mesure).Dans l’Encyclopédie (1751), Jean le Rond d’Alembert (1717 ; 1783) définit la trigonométrie comme

« l’art de trouver les parties inconnues d’un triangle par le moyen de celles qu’on connaît ».

C’est bien la démarche qui est demandée aux élèves du collège.

1. Relation trigonométrique dans le triangle rectangle :

Théorème:

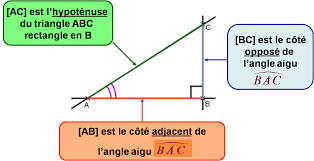
Dans un triangle rectangle ABC, on peut définir la relation suivante entre les angles aigus et les différentes longueurs des côtés.

Le cosinus d’un angle aigu est donné par :

$cos(\widehat{BAC})=\frac{Adjacent}{Hypotenuse}$

soit :

$cos(\widehat{BAC})=\frac{AB}{AC}$

Moyen mnémotechnique :

CAH ( Cosinus = Adjacent/Hypoténuse )

Remarques :
Le cosinus d’un angle aigu est toujours compris entre – 1 et 1.

Exemples :

Si AB=16 cm et BC=20 cm, calculer $cos\,(\widehat{ABC})$

[ Réponse : $cos(\widehat{ABC})=0,8$ ]

Si AB=3 cm et BC= 12 cm, calculer $cos(\widehat{ABC})$

[ Réponse : $cos(\widehat{ABC})\,=\,0,25$ ]

2. Détermination de la mesure d’un angle en degré, connaissant son cosinus :

Méthode :

La détermination de la mesure d’un angle connaissant son cosinus s’effectue à l’aide de la calculatrice :

Vérifier que la calculatrice est en mode degré (DEG);
Utiliser la touche $x=cos^{-1}$ ou pour extraire la mesure de l’angle en degré.

Exemples :

Si $cos\,x=0,5$ alors $x=cos^{-1}(0,5)=60^{\circ}$ .

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «cosinus d’un angle aigu et trigonométrie : cours de maths en 4ème en PDF.» au format PDF.

D'autres cours et exercices à consulter

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.