DIPLÔME NATIONAL DU BREVET
SESSION 2017
PREMIÈRE ÉPREUVE
1ère partie
MATHÉMATIQUES
Série générale
Durée de l’épreuve : 2 heures – 50 points
Présentation de la copie et utilisation de la langue française 5 points
Toutes les réponses doivent être justifiées, sauf si une indication contraire est donnée.
Pour chaque question, si le travail n’est pas terminé, laisser tout de même une trace de la
recherche. Elle sera prise en compte dans la notation.
THÉMATIQUE COMMUNE DE L’ÉPREUVE DE MATHÉMATIQUES-SCIENCES : L’EAU
Exercice 1 : 6 points
Un sac opaque contient 120 boules toutes indiscernables au toucher, dont 30 sont bleues. Les autres boules sont rouges ou vertes.
On considère l’expérience aléatoire suivante :
On tire une boule au hasard, on regarde sa couleur, on repose la boule dans le sac et on mélange.
1. Quelle est la probabilité de tirer une boule bleue ? Écrire le résultat sous la forme d’une fraction
irréductible.
2. Cécile a effectué 20 fois cette expérience aléatoire et elle a obtenu 8 fois une boule verte. Choisir, parmi les réponses suivantes, le nombre de boules vertes contenues dans le sac (aucune justification n’est demandée) :
a. 48 b. 70 c. On ne peut pas savoir d. 25
3. La probabilité de tirer une boule rouge est égale à 0,4.
a. Quel est le nombre de boules rouges dans le sac ?
b. Quelle est la probabilité de tirer une boule verte ?
Exercice 2 : 7 points
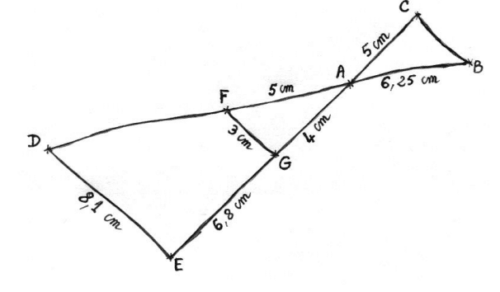
Pour illustrer l’exercice, la figure ci-dessous a été faite à main levée.
Les points D, F, A et B sont alignés, ainsi que les points E, G, A et C.
De plus, les droites (DE) et (FG) sont parallèles.
1. Montrer que le triangle AFG est un triangle rectangle.
2. Calculer la longueur du segment [AD]. En déduire la longueur du segment [FD].
3. Les droites (FG) et (BC) sont-elles parallèles ? Justifier.
Exercice 3 : 6 points
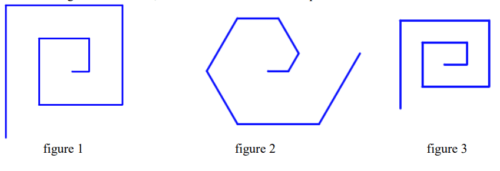
Voici trois figures différentes, aucune n’est à l’échelle indiquée dans l’exercice :
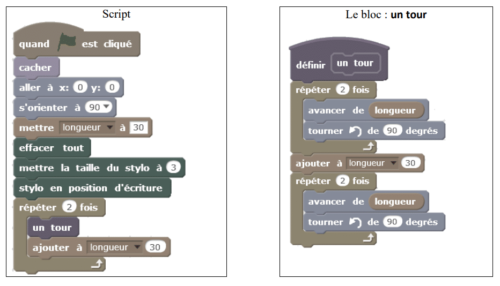
Le programme ci-dessous contient une variable nommée « longueur ».
On rappelle que l’instruction 
1. a. Dessiner la figure obtenue avec le bloc « un tour » donné dans le cadre de droite ci-dessus, pour une
longueur de départ égale à 30, étant orienté vers la droite avec le stylo, en début de tracé.
On prendra 1 cm pour 30 unités de longueur, c’est-à-dire 30 pixels.
b. Comment est-on orienté avec le stylo après ce tracé ? (aucune justification n’est demandée)
2. Laquelle des figures 1 ou 3 le programme ci-dessus permet-il d’obtenir ? Justifier votre réponse.
3. Quelle modification faut-il apporter au bloc « un tour » pour obtenir la figure 2 ci-dessus ?
Exercice 4 : 9 points
Monsieur Chapuis souhaite changer le carrelage et les plinthes(*) dans le salon de son appartement. Pour cela il doit acheter des carreaux, de la colle et des plinthes en bois qui seront clouées. Il dispose des documents suivants :
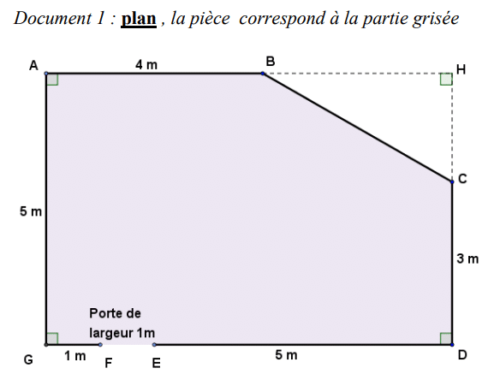
1. a. En remarquant que la longueur GD est égale à 7m, déterminer l’aire du triangle BCH.
b. Montrer que l’aire de la pièce est 32 m².
2. Pour ne pas manquer de carrelage ni de colle, le vendeur conseille à monsieur Chapuis de prévoir une
aire supérieure de 10 % à l’aire calculée à la question 1.
Monsieur Chapuis doit acheter des boîtes entières et des sacs entiers.
Déterminer le nombre de boîtes de carrelage et le nombre de sacs de colle à acheter.
3. Le vendeur recommande aussi de prendre une marge de 10% sur la longueur des plinthes. Déterminer le nombre total de plinthes que monsieur Chapuis doit acheter pour faire le tour de la pièce. On précise
qu’il n’y a pas de plinthe sur la porte.
4. Quel est le montant de la dépense de monsieur Chapuis, sachant qu’il peut se contenter d’un paquet de clous ? Arrondir la réponse à l’euro près.
Exercice 5 : 5 points
Pour chaque affirmation, dire en justifiant, si elle est vraie ou fausse.
Exercice 6 : 5 points

Chaque canon à neige utilise 1 m3 d’eau pour produire 2 m3 de neige.
Débit de production de neige : 30 m3 par heure et par canon.
1. Pour préparer correctement la piste de slalom, on souhaite produire une couche de neige artificielle de 40 cm d’épaisseur.
Quel volume de neige doit-on produire ? Quel sera le volume d’eau utilisé ?
2. Sur cette piste de ski, il y a 7 canons à neige qui produisent tous le même volume de neige.
Déterminer la durée nécessaire de fonctionnement des canons à neige pour produire les 4 800 m
3 de neige souhaités. Donner le résultat à l’heure près.
Exercice 7 : 7 points
Les légionelles sont des bactéries présentes dans l’eau potable. Lorsque la température de l’eau est comprise
entre 30°C et 45°C, ces bactéries prolifèrent et peuvent atteindre, en 2 ou 3 jours, des concentrations
dangereuses pour l’homme.
On rappelle que « μm » est l’abréviation de micromètre. Un micromètre est égal à un millionième de mètre.
1. La taille d’une bactérie légionelle est 0,8 micromètre.
Exprimer cette taille en m et donner le résultat sous la forme d’une écriture scientifique.
2. Lorsque la température de l’eau est 37°C, cette population de bactéries légionelles double tous les quarts d’heure.
Une population de 100 bactéries légionelles est placée dans ces conditions.
On a créé la feuille de calcul suivante qui permet de donner le nombre de bactéries légionelles en
fonction du nombre de quarts d’heure écoulés :
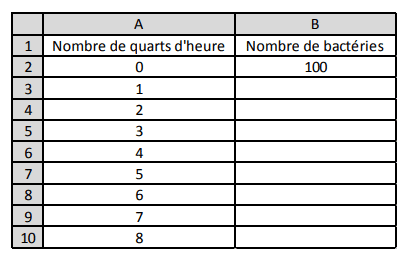
a. Dans la cellule B3, on veut saisir une formule que l’on pourra étirer vers le bas dans la colonne B
pour calculer le nombre de bactéries légionelles correspondant au nombre de quarts d’heure
écoulés. Quelle est cette formule ?
b. Quel est le nombre de bactéries légionelles au bout d’une heure ?
c. Le nombre de bactéries légionelles est-il proportionnel au temps écoulé ?
d. Après combien de quarts d’heure cette population dépasse-t-elle dix mille bactéries légionelles ?
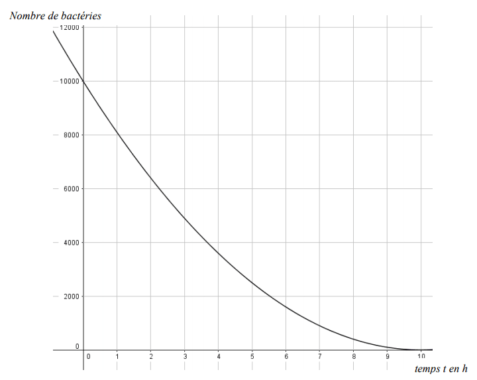
3. On souhaite tester l’efficacité d’un antibiotique pour lutter contre la bactérie légionelle. On introduit
l’antibiotique dans un récipient qui contient 104 bactéries légionelles au temps = 0. La représentation
graphique, sur l’annexe , à rendre avec la copie, donne le nombre de bactéries dans le récipient en
fonction du temps.
a. Au bout de 3 heures, combien reste-t-il environ de bactéries légionelles dans le récipient ?
b. Au bout de combien de temps environ reste-t-il 6000 bactéries légionelles dans le récipient ?
c. On estime qu’un antibiotique sera efficace sur l’être humain s’il parvient à réduire de 80% le nombre
initial de bactéries dans le récipient en moins de 5 heures.
En s’aidant du graphique, étudier l’efficacité de l’antibiotique testé sur l’être humain.
Annexe à rendre avec la copie
Faire apparaître les traits justifiant les réponses de la question 3. de l’Exercice 7.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «france rattrapage septembre 2017 – sujet et corrigé du brevet de maths» au format PDF.
D'autres cours et exercices à consulter
- Sujet 2018 France du brevet de maths des collèges
- Brevet Asie Pacifique 2016 : sujet et corrigé en PDF.
- Brevet Amérique du Nord 2021 maths : sujet et corrigé en PDF.
- Asie et Pacifique : brevet de maths 2022 avec sujet et corrigé
- Brevet Maths 2021 : sujet corrigé blanc pour la révision du DNB
- Brevet 2016 aux centres étrangers : sujet et corrigé
- Brevet de maths 2016 : sujet blanc pour réviser en PDF.
- Asie Pacifique : brevet de maths 2024 avec sujet et corrigé en PDF.