Brevet de mathématiques
Session 2017
Asie Pacifique
Exercice 1 : (4 points)
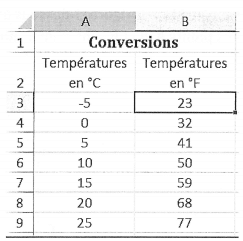
Aux États-Unis, la température se mesure en degré Fahrenheit (en °F).
En France, elle se mesure en degré Celsius (en °C).
Pour faire les conversions d’une unité à l’autre, on a utilisé un tableur,
Voici une copie de l’écran obtenu ci-contre :
1)Quelle température en °F correspond à une température de 20 °C?
2) Quelle température en °C correspond à une température de 4L « F ?
3) Pour convertir la température de °C en °F, il faut multiplier la température en oC par
1,8 puis ajouter 32.
On a écrit une formule en 83 puis on l’a recopiée vers le bas.
Quelle formule a-t-on pu saisir dans la cellule B3 ?
Exercice 2 (5 points)
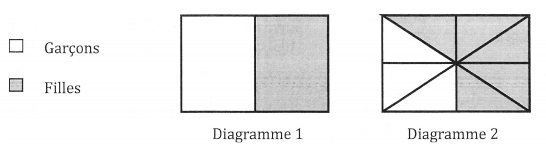
Dans une classe de 24 élèves, il y a 1,6 filles.
1) L un des deux diagrammes ci-dessous peut-il représenter correctement la répartition des élèves de cette classe ?
2) On a représenté la répartition des élèves de cette classe par un diagramme circulaire.
Écrire le calcul permettant de déterminer la mesure de I’angle du secteur qui représente
les garçons.
Exercice 3 (6 points)
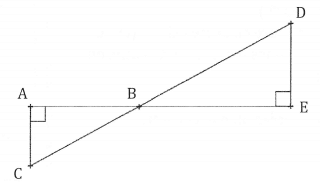
On considère la figure ci-dessous qui n’est pas représentée en vraie grandeur.
Les points A, B et E sont alignés ainsi que les points C, B et D.
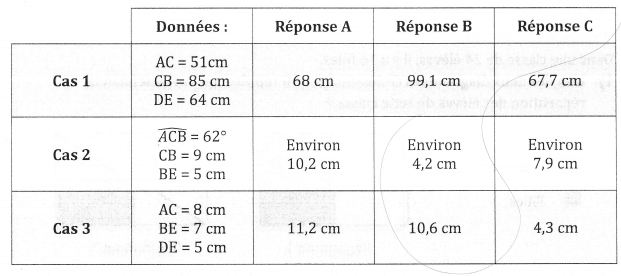
1) Dans chacun des cas suivants, indiquer sur la copie la réponse qui correspond à la
longueur du segment [AB] parmi les réponses proposées. Aucune justification n’est attendue.
2) Pour l’un des trois cas uniquement, au choix justifier la réponse sur la copie en
rédigeant.
Exercice 4 (4 points)
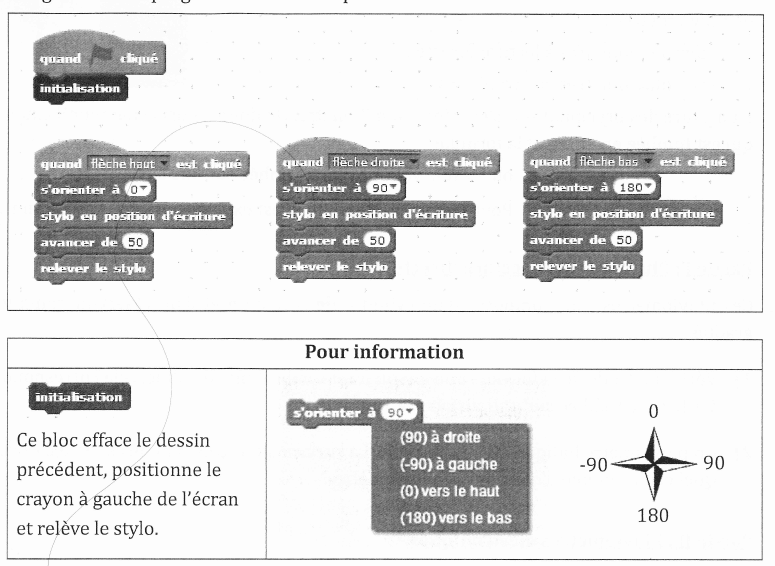
Margot a écrit le programme suivant. Il permet de dessiner avec trois touches du clavier.
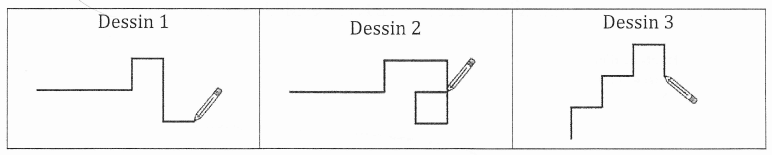
1) Parmi les trois dessins suivants, un seul ne pourra pas être réalisé avec ce programme.
Lequel ? Expliquer
2) Julie a modifié le programme de Margot (voir ci-dessous).
Que devient alors le dessin 3 avec le programme modifié par Julie ?
Exercice 5 (8 points)
Pour mesurer les précipitations, Météo France utilise deux sortes de pluviomètres :
– des pluviomètres à lecture directe ;
– des pluviomètres électroniques.

La mesure des précipitations s’exprime millimètre. On donne ainsi la hauteur d’eau H en qui est tombée en utilisant la formule :
où V est le volume d’eau tombée sur une surface S.
Pour H exprimée en mm , V est exprimé en et S en
.
Partie I: Pluviomètres à lecture directe.
Ces pluviomètres sont composés d’un cylindre de réception et d’un réservoir conique gradué.
1) Vérifier à l’aide de la formule que lorsqu’il est tombé 1 mm de pluie, cela correspond a 1 L d’eau tombée sur une surface
de 1 m².
2) Un pluviomètre indique 10 mm de pluie. La surface qui reçoit la pluie est de 0,01 m².
Quel est le volume d’eau dans ce pluviomètre ?
Partie II : Pluviomètres électroniques.
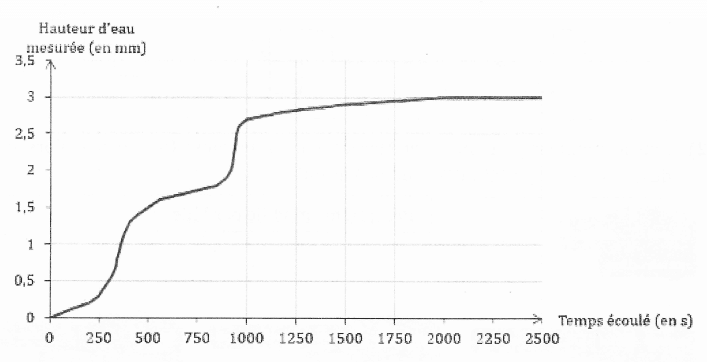
Durant un épisode pluvieux, on a obtenu le graphique suivant grâce à un pluviomètre électronique.
1) L’épisode pluvieux a commencé à 17h15.
Vers quelle heure la pluie s’est-elle arrêtée?
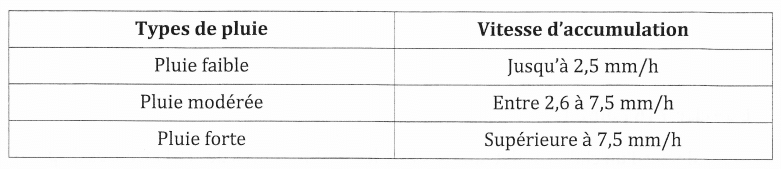
2) On qualifie les différents épisodes pluvieux de la façon suivante :
À l’aide des informations données par le graphique et le tableau ci-dessus, cette pluie
serait-elle qualifiée de faible, modérée ou forte ?
Exercice 6 (7 points)
Gaspard réalise des motifs avec des carreaux de mosaïque blancs et gris de la façon
suivante :
Gaspard forme un carré avec des carreaux gris puis le borde avec des carreaux blancs.
1) Combien de carreaux blancs Gaspard va-t-il utiliser pour border le carré gris du motif 4 (un carré ayant 4 carreaux gris de côté) ?
2) a) justifier que Gaspard peut réaliser un motif de ce type en utilisant exactement 144 carreaux gris.
b) Combien de carreaux blancs utilisera-t-il alors pour border le carré gris obtenu ?
3) On appelle « motif n » le motif pour lequel on borde un carré de n carreaux gris de côté,
Trois élèves ont proposé chacun une expression pour calculer le nombre de carreaux blancs nécessaires pour réaliser le « motif n » :
Expression n° 1- :
Expression n° 2 :
Expression n° 3 :
Une seule de ces trois expressions ne convient pas. Laquelle ?
Exercice 7 (6 points)
L’entraîneur d’un club d’athlétisme a relevé les performances de ses lanceuses de poids sur cinq lancers.
Voici une partie des relevés qu’il a effectués (il manque trois performances pour une des lanceuses) :
On connaît des caractéristiques de la série d’une des lanceuses :
1) Expliquer pourquoi ces caractéristiques ne concernent ni les résultats de Solenne, ni ceux de Rachida.
2) Les caractéristiques données sont donc celles de Sarah. Son meilleur lancer est de 19,5 m.
Indiquer sur la copie quels peuvent être les trois lancers manquants de Sarah ?
Exercice 8 ( 5 points)
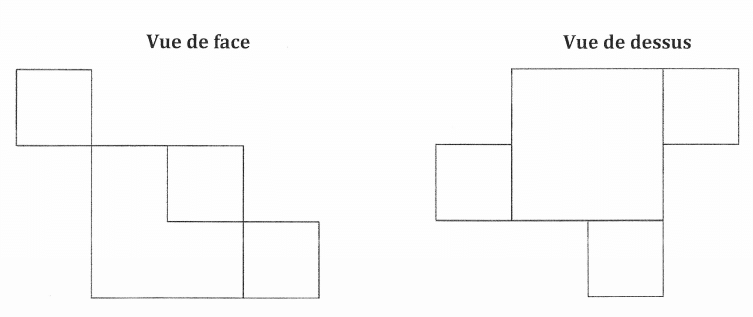
La figure ci-dessous représente un solide constitué de l’assemblage de quatre cubes :
– trois cubes d’arête 2 cm;
– un cube d’arête 4 cm.
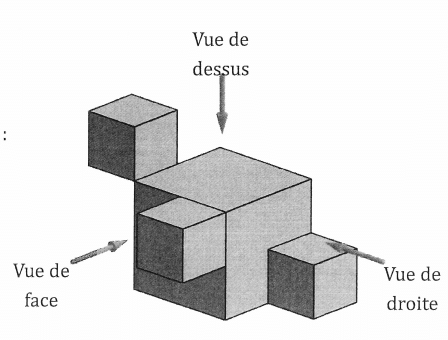
1) Quel est le volume de ce solide ?
2) on a dessiné deux vues de ce solide face (elles ne sont pas en vraie grandeur).
Dessiner la vue de droite de ce solide en vraie grandeur.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «asie Pacifique 2017 : sujet et corrigé du brevet maths en PDF» au format PDF.
D'autres cours et exercices à consulter
- Amérique du nord 2016 : sujet du brevet de maths
- Sujet 2018 France du brevet de maths des collèges
- Conseils pour réussir son brevet de maths 2023.
- Brevet de maths 2021 : sujet blanc n° 3 en PDF
- Asie Pacifique : brevet de maths 2024 avec sujet et corrigé en PDF.
- Brevet Maths 2022 : sujet et corrigé à télécharger en PDF
- Brevet de maths 2024 aux centres étrangers avec sujet et corrigé.
- Asie 2019 : brevet de maths avec sujet et corrigé